大胖子走迷宫【spfa跑状态】【到这个点，并且这个胖 = max（到这个点，按照时间变的这个胖）

大胖子走迷宫

题意

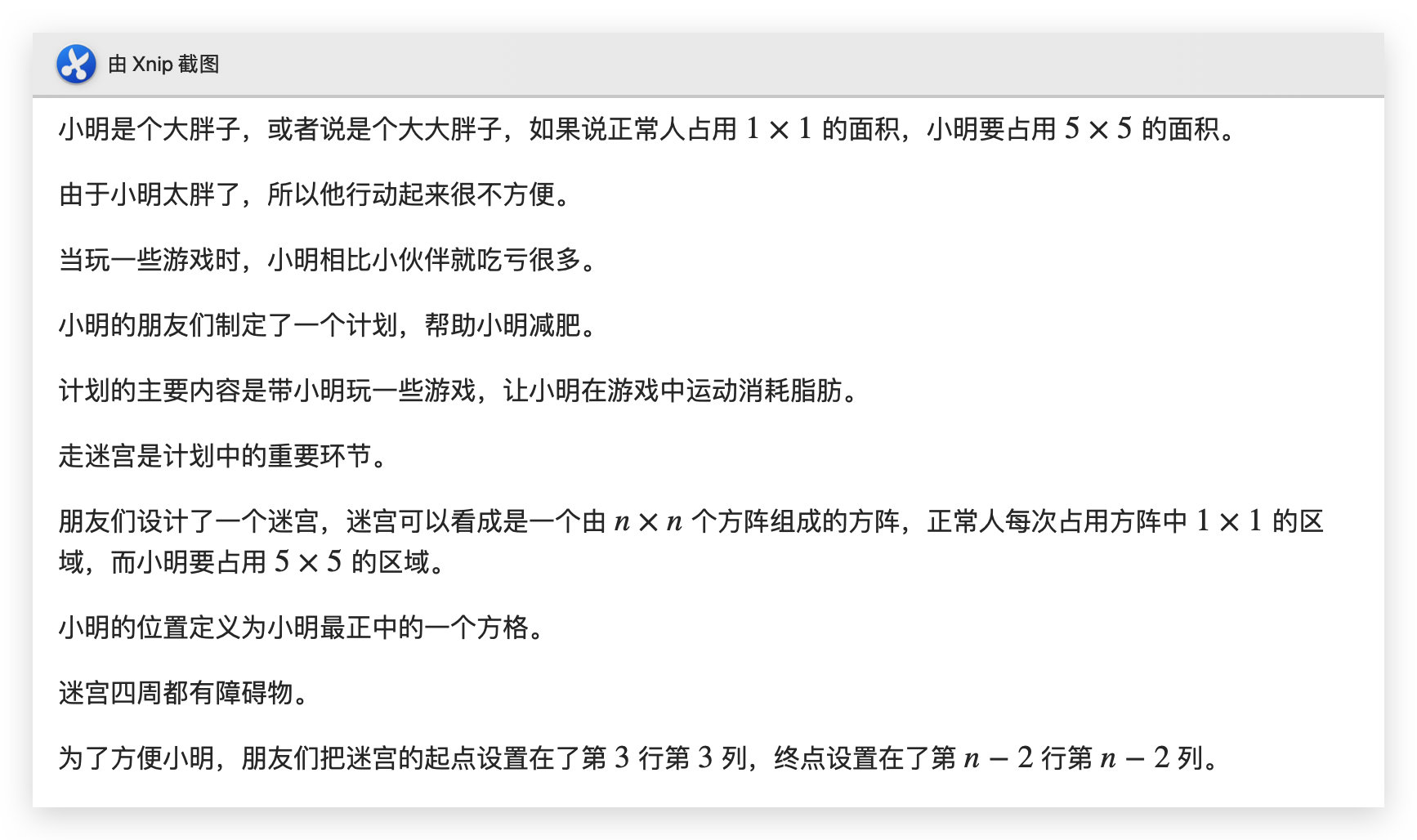
思路

普通的bfs走迷宫，多加了一个熟悉，就是胖的圈数。可以来回走，普通的bfs可能不太好处理，我们把这些状态放进spfa跑。

状态定义为{x,y,fat}:坐标位置，胖的圈数。

在状态转移时，因为可以原地走，所以共有5个方向。

接下来考虑，状态转移时花费的距离

• 要考虑是不是原地走，是不是要加1
• 要考虑fat维度（由胖到瘦花费的距离）
  • 由胖到瘦花费的距离是固定的。
  • 我们想求出转移到的状态的距离，要记得和上面的取个max。
• 总之：到达这个点，并且还是这么“胖”的花费 = max（到达这个点的花费，变的这么胖的花费）

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<vector>
#include<stack>
#include<bitset>
#include<cstdlib>
#include<cmath>
#include<set>
#include<list>
#include<deque>
#include<map>
#include<queue>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define mst(s,_s) memset(s, _s, sizeof(s))
const double PI = acos(-1.0);
const double eps = 1e-6;
const int INF = 0x3f3f3f3f;
const int N = 1e3+100;
int T,n,m;
char g[N][N];
int st[N][N][3];
int dis[N][N][3];
struct node{
    int x,y,fat;
};
int dx[5]={-1,0,1,0,0},dy[5]={0,1,0,-1,0};
bool judge(int x, int y, int z)
{
    for(int i = x - z; i <= x + z; i ++)
    {
        if(i < 1 or i > n)  return false;
        for(int j = y - z; j <= y + z; j ++)
        {
            if(j < 1 or j > n)  return false;
            if(g[i][j] == '*')  return false;
        }
    }
    return true;
}
int spfa()
{
    memset(dis,0x3f,sizeof dis);
    dis[3][3][2]=0;
    queue<node>q;
    q.push({3,3,2});
    st[3][3][2]=1;
    while(q.size())
    {
        auto t=q.front();
        q.pop();
        int x=t.x,y=t.y,z=t.fat;
        st[x][y][z]=0;
        for(int i=0;i<5;i++)
        {
            int a=x+dx[i];
            int b=y+dy[i];
            int c=z;

            int dist=(i!=4) + dis[x][y][z];
            while(c>=0)
            {   

                dist=max(dist,(2-c)*m+1);
                if(judge(a,b,c))
                    if(dist<dis[a][b][c])
                    {
                        dis[a][b][c]=dist;
                        if(!st[a][b][c]) {
                            q.push({a,b,c});
                            st[a][b][c]=1;
                        }

                    }
                c--;

            }
        }

    }
    int res=0x3f3f3f3f;
    for(int i=0;i<=2;i++) res=min(res,dis[n-2][n-2][i]);
    return res;
}
int main() {
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>g[i]+1;

    cout<<spfa()<<endl;

    return 0;
}