[树结构]平衡二叉树AVL

平衡二叉树是一种二叉排序树，其中每一个节点的左子树和右子树的高度至多等于1，平衡二叉树又称为AVL树。

将二叉树节点的左子树深度减去右子树深度的值称为平衡因子BF，平衡二叉树上所有节点的平衡因子只可能是-1,0或者1。

距离插入点最近的，且平衡因子的绝对值大于1的结点为根的子树，我们称为最小不平衡子树。

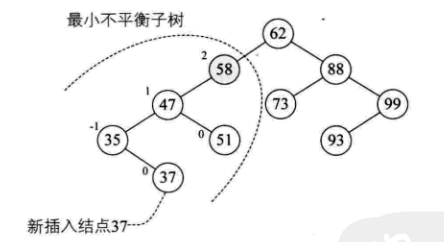
平衡二叉树实现原理

先来看一个例子：

对于数组a[10]={3,2,1,4,5,6,7,10,9,8}构建平衡二叉树。

按照二叉排序树的方式插入新的元素，当插入1的时候，使得当前二叉树失去平衡：

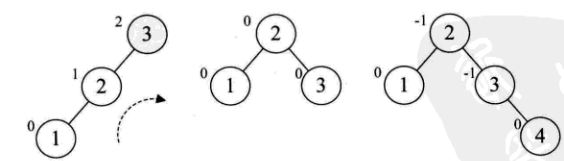
当插入5的时候，使得平衡二叉树再次失去平衡：

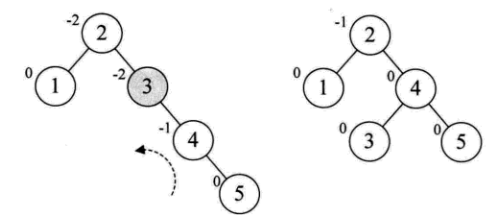
插入6的时候，同样产生不平衡：

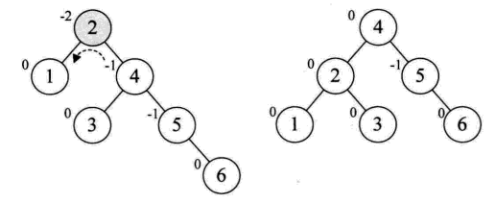
注意：上面的这些不平衡都有一个共同的特点，那就是最小不平衡子树的根的BF同它的孩子（左孩子或者右孩子）的BF是同号的。所以这是仅需要一次旋转就可以了。

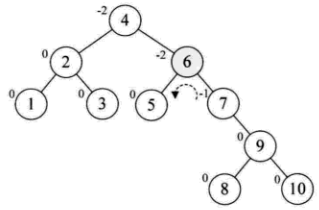
当插入到数字9的时候，同样的发生了不平衡：

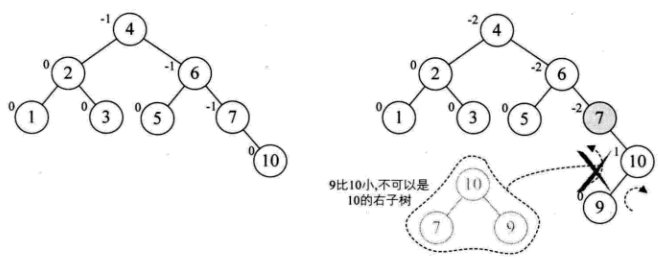
从上面的图可以看到一次的旋转是不能做到再次的平衡的。所以要两次旋转。

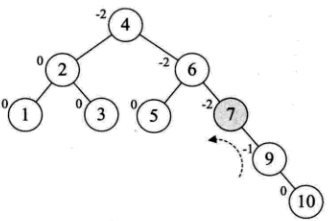
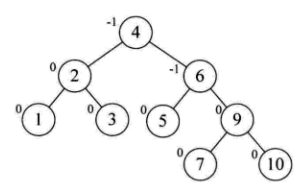
在插入8的时候，同样的发生了不平衡，同样的需要两次调整：

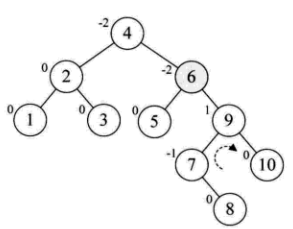
所以总结上面的过程：

当最小不平衡子树根节点的平衡因子BF是大于1的时候，就右旋，小于-1时就左旋。

插入节点后，最小不平衡子树的BF与它的子树的BF符号相反时，就需要对子树节点先进行一次旋转，以使得符号相同后，在反向旋转一次才能够完成平衡操作。

平衡二叉树算法实现

加入了平衡因子，所以在每一个结点中增加一个数据域，这个数据域表示以这个结点为根的二叉树的平衡因子。所以树结点的定义为：

typedef struct BiTNode
{
	int data;
	int bf;
	struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

其实对于二叉平衡树的每一次的调整都可以分成两个步骤：

• 调整各个结点的BF值
• 旋转子树结构

先写旋转子树结构代码：

void R_Rotate(BiTree *T)
{
	BiTree tmp;
	tmp = (*T)->lchild;
	(*T)->lchild = tmp->rchild;
	tmp->rchild = (*T);
	*T = tmp;
}

void L_Rotate(BiTree *T)
{
	BiTree tmp;
	tmp = (*T)->rchild;
	(*T)->rchild = tmp->lchild;
	tmp->lchild = (*T);
	*T = tmp;
}

所以当插入一个新的结点，导致树结构不平衡的时候，当树右边超重的时候，要右平衡：（树主体左旋转）

//右平衡，右子树超重
void RightBalance(BiTree *T)
{
	BiTree tmp, tmpr;
	tmp = (*T)->rchild;
	switch (tmp->bf)
	{
	case -1:
		(*T)->bf = 0;
		tmp->bf = 0;
		L_Rotate(T);
		break;
	case 1:
		tmpr = tmp->lchild;
		switch (tmpr->bf)
		{
		case 1:
			tmp->bf = -1;
			(*T)->bf = 0;
			break;
		case -1:
			tmp->bf = 0;
			(*T)->bf = 1;
			break;
		case 0:
			tmp->bf = (*T)->bf = 0;
		}

		tmpr->bf = 0;
		//R_Rotate(&tmp);是错误的，因为不能修改上一级的指针
		R_Rotate(&(*T)->rchild);
		L_Rotate(T);
	}
}

当插入一个结点导致树结构不平衡的时候，左子树超重，要左平衡：（树主体右旋转）

//左平衡，左子树超重
void LeftBlance(BiTree *T)
{
	BiTree tmp,tmpr;
	tmp = (*T)->lchild;
	switch (tmp->bf)
	{
	case 1:
		(*T)->bf = 0;
		tmp->bf = 0;
		R_Rotate(T);
		break;
	case -1:
		tmpr = tmp->rchild;
		switch (tmpr->bf)
		{
		case 1:
			tmp->bf = 0;
			(*T)->bf = -1;
			break;
		case -1:
			tmp->bf = 1;
			(*T)->bf = 0;
			break;
		case 0:
			(*T)->bf = 0;
			tmp->bf = 0;
			break;
		}//switch

		tmpr->bf = 0;
		//L_Rotate(&tmp);是错误的，因为不能修改上一级的指针
		L_Rotate(&(*T)->lchild);
		R_Rotate(T);
	}
}

注意：上面两处的双旋转的时候，不能旋转tmp，因为这样不能把父结点的指针修改，所以要旋转父结点指下来得指针。

最后插入操作的主函数：

bool InsertAVL(BiTree *T, int key, bool *taller)
{
	if (*T ==NULL)
	{
		*T = (BiTree)malloc(sizeof(BiTNode));
		(*T)->data = key;
		(*T)->lchild = (*T)->rchild = NULL;
		(*T)->bf = 0;
		*taller = true;

		return true;
	}

	if((*T)->data == key)
	{
		*taller = false;
		return false;
	}
	else if((*T)->data > key)
	{
		if(!InsertAVL(&(*T)->lchild, key, taller))
			return false;
		if(*taller)
		{
			switch ((*T)->bf)
			{
			case 1:
				LeftBlance(T);
				*taller = false;
				break;
			case 0:
				(*T)->bf = 1;
				*taller = true;
				break;
			case -1:
				(*T)->bf = 0;
				*taller = false;
				break;
			}//switch
		}//if
	}//else if
	else	//(*T)->data < key
	{
		if (!InsertAVL(&(*T)->rchild, key, taller))
			return false;
		if(*taller)
		{
			switch ((*T)->bf)
			{
			case 1:
				(*T)->bf = 0;
				*taller = false;
				break;
			case 0:
				(*T)->bf = -1;
				*taller = true;
				break;
			case -1:
				RightBalance(T);
				*taller = false;
			}//switch
		}//if
	}//else

	return true;
}