【五一qbxt】day4 数论知识

这些东西大部分之前都学过了啊qwq

zhx大概也知道我们之前跟着他学过这些了qwq，所以：

先讲新的东西qwq：（意思就是先讲我们没有学过的东西）

进制转换

10=2³+2¹=1010_（2）

=3²+3⁰=101_（3）

进制转换的两种操作：

1.10进制=>k进制

短除法：

55_（10）：

55/3=18……1

18/3=6…… 0

6/3=2…… 0

2/3=0…… 2

55_（10）=2001_（3）

2.k进制=>10进制

k进制数x，n~0

x_nx_n-1x_n-2……x_0（k）

= x_n*kⁿ+x_n-1*k^n-1+x_n-2*k^n-2……x₀*k⁰

特殊的进制：

二进制  想要的二进制表示前+0  举个栗子：01001 c++识别为9

八进制

十进制

十六进制  想要直接写16进制数+0x  举个栗子：0x1001=16 ³+16⁰=4097；10~15：用字母代表 A=10,B=11,C=12……F=15

0x3f3f3f3f= 3*16⁷+15*16⁶+3*16⁵+15*16⁴+3*16³+15*16²+3*16¹+15*16⁰

高精度：

int -2³¹~2³¹-1

long long -2⁶³~2⁶³-1≈10²⁰

目的：解决大数运算

方法：竖式加减乘除法

加法：个位对齐，逐位相加。

2333+233=2566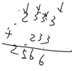 

储存：

19260817

从0~n，存从最高位到最低位✘  对不齐（麻烦）

0=>n 存 个位=>最高位

这时个位一定对齐的，逐位相加就可以了qwq

乘法：

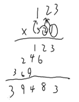
回到数论qwq：

质数：

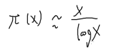
素数判定：O(根号n)

证明啊qwq：

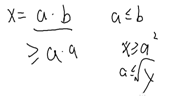
筛法：

#include<iostream>

for(int i=2;i<=n;i++)

for(int  b=i*2;b<=n;b+=i)

not_prime[b]=true;

约等于=n(1+1/2+1/3+……+1/n);调和级数

约等于nlogn

埃氏筛：

O（nloglogn）

一个合数，一定会被筛质数的倍数是被筛掉

for(int i=2;i<=n;i++)

if(not_prime[i] =false) //只筛掉质数的倍数

for(int  b=i*2;b<=n;b+=i)

not_prime[b]=true;

线性筛：（保证每个数只被最小的质因数筛掉）

memset(not_prime,0,sizeof(not_prime));

not_prime[1]=true;

for(int i=2;i<=n;i++){}

if(!not_prime[i])prime[++prime_count]=i;

for(int  j=1;j<=prime_count;j++){

if(prime[j]*i>n)break;

not_prime[prime[j]*i]=true;

if(i%prime[j]==0)break;//保证每个数只被筛一次且是被他最小质因子筛掉；

}

}

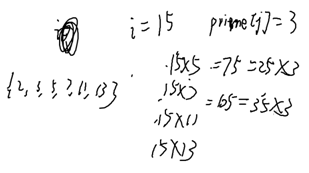
gcd：

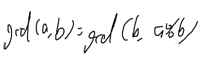
int gcd(int a,int b){

if(b==0) return a;

else return gcd(b,a%b);

}

内置函数：__gcd（下划线下划线gcd）（最好不要用）

扩展欧几里得算法qwq

令gcd(a,b)=g；

那么ax+by=g；

现在已知gcd(a,b)=g;

求得ax+by=g的一组解；

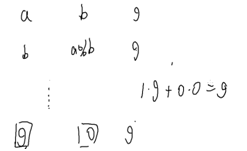
逆元：

费马小：

（mod p）

欧拉定理：

（mod m）

gcd（a，m）=1；

φ（m），有几个数和m是互质的：

m分解质因数：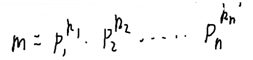

φ（m）= 

费马小是欧拉的特殊形式qwq

mod m，m不是质数；

/x  <=>  *x^φ（m）-1（mod m）

end-