[CSP-S模拟测试]:f（Trie树+二分答案+meet in middle+two pointers）

题目传送门（内部题67）

---

输入格式

第一行，三个整数$n$、$k$、$p$。
第二行，$n$个自然数，表示$\{a_i\}$。

---

输出格式

输出一行，两个自然数，表示$f(res)$、$res$。

---

样例

样例输入1：

4 3 5
2 0 3 7

样例输出1：

4 4

样例输入2：

2 2 1
2 0

样例输出2：

0 2

---

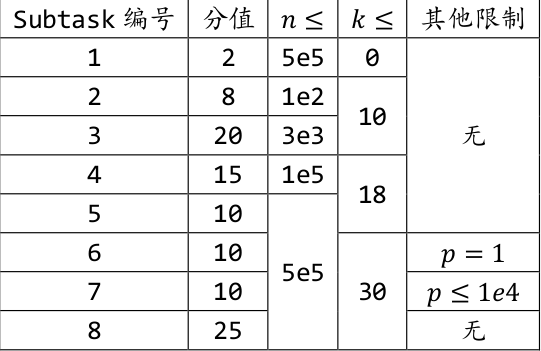
数据范围与提示

本题有$spj$，输出格式正确的情况下，仅回答正确$f(res)$、$res$中的一个可以获得$60\%$的分数（向下取整）。

---

题解

考虑怎样才能形成逆序对，或怎样才能让本身的逆序对消失。

设$a,b$，将其分解为二进制，我们只有改变其最高的不同位才能改变其大小关系；若对于其最高的不同位$a$为$0$，$b$为$1$，那么如果$xor$一个这一位是$1$的数，则其大小关系会改变，反之同理。

所以考虑$Trie$，将每一个$a_i$分解成二进制插入并计算贡献即可。

这样的算法是$55$分的。

考虑如何优化，部分正确提示了可以二分。

二分逆序对的个数即可，最后再用二分出来的值返回去找$res$即可。

时间复杂度：$\Theta(\log n^2\times 2^{\frac{k}{2}})$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int k;
long long n,p;
int trie[20000000][2],cnt=1;
long long sum[20000000][2],num[20000000];
long long ans;
long long val;
long long que[3000001];
pair<long long,int> f1[3000001],f2[3000001];
void insert(int x)
{
	int p=0;
	for(int i=k-1;i>=0;i--)
	{
		if(!trie[p][(x>>i)&1])trie[p][(x>>i)&1]=++cnt;
		sum[i][(x>>i)&1]+=num[trie[p][((x>>i)&1)^1]];
		p=trie[p][(x>>i)&1];
		num[p]++;
	}
}
bool judge(long long x)
{
	long long res=0;
	int fail=(1<<(k-k/2));
	for(int i=0;i<(1<<(k/2))&&f1[i].first<=x;i++)
	{
		while(x-f1[i].first<=f2[fail-1].first&&fail)fail--;
		res+=fail;
	}
	if(res<p){val=res;return 1;}
    return 0;
}
long long getans()
{
	int fail=(1<<(k-k/2))-1;
	for(int i=0;i<(1<<(k/2))&&f1[i].first<=ans;i++)
	{
		long long x=ans-f1[i].first;
		while(x<f2[fail].first&&fail>=0)fail--;
		if(f2[fail].first==x)que[++que[0]]=f1[i].second+(1<<(k/2))*f2[fail].second;
	}
	sort(que+1,que+que[0]+1);
	return que[p-val];
}
int main()
{
	scanf("%lld%d%lld",&n,&k,&p);
	for(int i=1;i<=n;i++)
	{
		int x;
		scanf("%d",&x);
		insert(x);
	}
	for(int i=0;i<(1<<(k/2));i++)
	{
		for(int j=0;j<(k/2);j++)f1[i].first+=sum[j][i>>j&1];
		f1[i].second=i;
	}
	for(int i=0;i<(1<<(k-k/2));i++)
	{
		for(int j=0;j<(k-k/2);j++)f2[i].first+=sum[j+k/2][i>>j&1];
		f2[i].second=i;
	}
	sort(f1,f1+(1<<(k/2)));
	sort(f2,f2+(1<<(k-k/2)));
	long long lft=0,rht=n*(n-1)/2;
	while(lft<=rht)
	{
		long long mid=(lft+rht)>>1;
		if(judge(mid)){lft=mid+1;ans=mid;}
		else rht=mid-1;
	}
	printf("%lld %lld",ans,getans());
	return 0;
}

---

rp++