qbzt day2 下午

内容提要

高精

矩阵

筛法

---

先是高精除法

注意细节

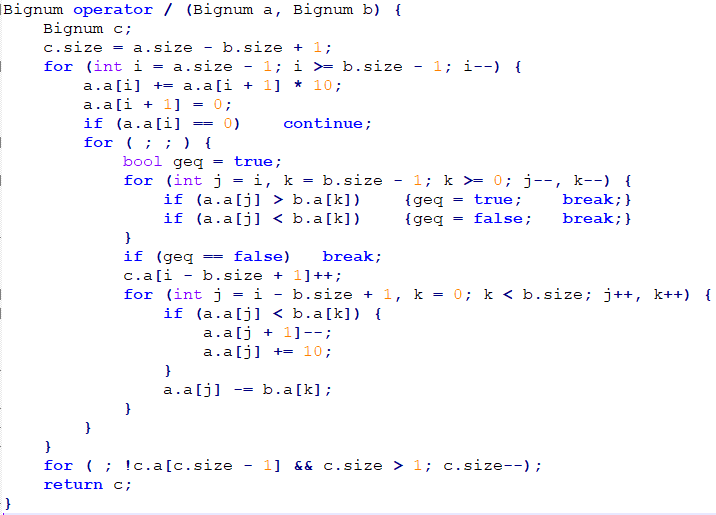
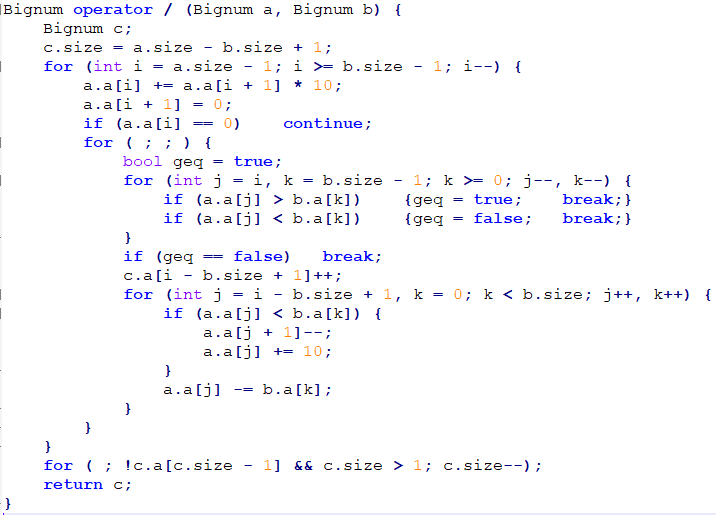
高精度开方：神奇的竖式

以小数点为分界线，每两个位砍一刀

87654.321-->08|76|54|.32|1

大概就是先对第一位开方，然后相减，将上面的数乘二十，看看加多少再乘多少正好不能撑爆剩下的数，就在上面写几，重复操作就ok

原理是： (a*10+b)^2=a^2+2*a*10*b+b^2=a^2+(20*a+b)*b

竖式算开平方步骤：（如：把625开方）

（1）先把被开方的数由右到左每二位一组。（6,25)

（2）由左到右取每一组。（取的是6）

（3）取某数的平方，要比第一组数小，但某数+1的平方，要比第一组数大，这就是第一个开方值。（某数是2）

（4）把第一组数减去第一个开方值的平方，再取第二组数，构成余数。（6-2*2=2，余数为225）

（5）把第一个开方值*20，再加上估计的第二个开方值，它与第二个开方值相乘要比余数小，但把第一个开方值*20，再加上估计的第二个开方值+1，它与第二个开方值+1相乘要比余数大。（第二个开方值取5，2*20+5=45，45*5=225)

所以(625)^0.5=25

现在中考高考都不让带计算器了，试卷上出现的一些常见开方的数字都是直接提供给学生的。现在手工列竖式开方基本不再需要了，但是每每想起当时老师教过的列式开平方的方法，还是很骄傲的。

手工开平方的原理实际是很简单的，原理如下

(a+b)^2=a^2+2ab+b^2=a^2+(2a+b)*b

这里的a取10的倍数，b取个位数，如(10+2)^2=10^2+(2*10+2)*2=100+22*2=144，这是知道结果时的推算，如何给你一个数字，让你推算它的开平方值呢？

现在要对144开平方，那么估计所求的值为十几，因此可以写成(10+?)^2=10^2+(2*10+?)*?，这样猜这个？为2时，再代入计算，发现计算出的值正确。按此方法，可以列竖式进行计算。如果需要对2025进行开方处理，那么按两位两位进位，需要先对20求根，取5时，5*5>20，因此只能取4，也就是结果是四十几，即(40+?)^2=40^2+(2*40+?)*?，即减去40的平方1600后，2025还余下425，425再去除于8？(八十几)，才能得到？（几），结论当然是85*5=425，因此2025开平方就是45。

。

快速幂

矩阵乘法

一个i行k列的矩阵乘一个k行j列的矩阵得到一个i行j列的矩阵

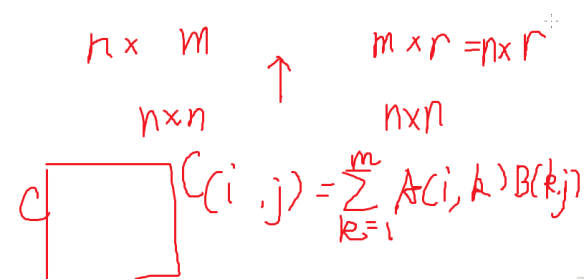
答案矩阵的第i，j个元素为A矩阵第i行第k个元素乘B矩阵第k行第j个元素，k是从1到m

就是一个矩阵的行乘另一个矩阵的列

代码：

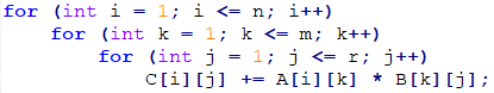
矩阵快速幂常用于求解线性递推方程组

比如斐波那契数列的矩阵就是

1  1

1  0

[f[n],f[n-1]]*[矩阵]^k=[f[n+k],[n+k-1]]

矩阵快速幂基于以下的原理，即可以找到一个矩阵 M

使得 [F(n-1) F(n)]T* M = [F(n) F(n+1)]T

以斐波拉期数列为例：M = ((1 1) (1 0))

以此类推：

[F(0) F(1)]T* Mn = [F(n) F(n+1)]T

我们成功将一个递推式转化成了一个求矩阵幂的问题

利用快速幂算法可以将时间缩短为 O(d^3logn)

利用 FFT + 矩阵特征多项式的黑科技可以把时间进一步缩短到 O(dlogdlogn)

我们来试着写一下下面的矩阵：

F(n) = 7F(n-1) + 6F(n-2) + 5n + 4 * 3^n

先考虑转换前后的两个矩阵，肯定要有所有在转换中需要的

我们发现如果要从f[n-1]转换到f[n]，要用到f[n-1],f[n-2],n,3^n，我们就先写上这些

然后发现n要转换到n+1就需要个1，再加上1就好了

[f[n-1,] f[n-2,] n, 3^n, 1]

[f[n], f[n-1], n+1, 3^(n+1) ,1]

然后按照递推式搞一搞就ok

高斯消元

高斯消元可以将一个矩阵变成一个上三角矩阵

在 OI 中一般用于两点：求解线性方程组（不常见） & 求线性基（常见）

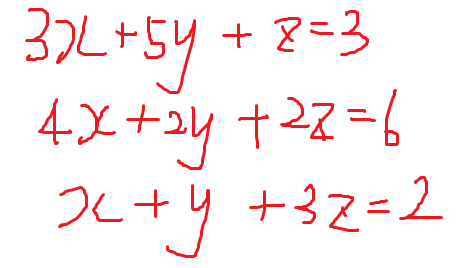
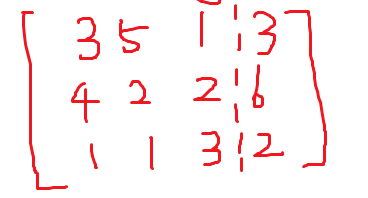
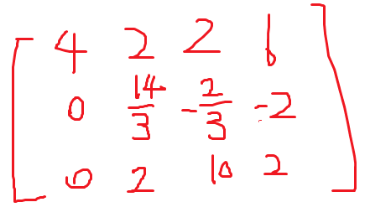
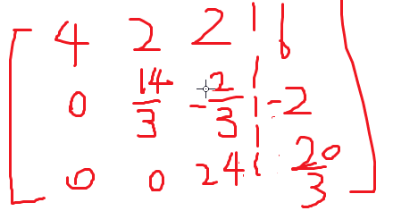
然后搞一搞就行

注意判断无解和无穷解的情况

线性基常见问题：

如何求一堆数的异或和中第 K 大的值？

筛法

常见的埃拉托斯特尼筛，复杂度为 O（nlogn），优化后达到O（nlognlogn）

欧拉筛

让每个合数被他的最小的质因子筛掉

欧拉筛还可以用来维护一些复杂的函数值

如：逆元、一个数的质因数分解中最大的指数的值

积性函数：对于所有互质的 x 和 y，F(x * y) = F(x) * F(y)

完全积性函数：对于所有 x 和 y ，F(x * y) = F(x) * F(y)

常见的积性函数：

欧拉函数 φ(n) ：不超过 n 与 n 互素的数的个数

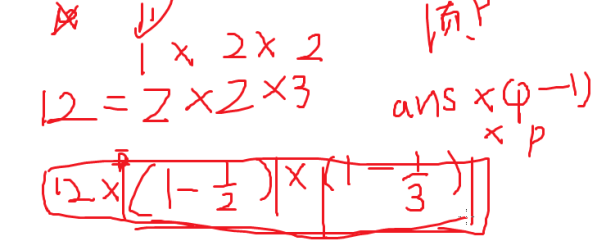
若

则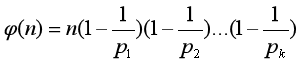

怎么用程序求φ？

欧拉筛，筛数i，选取一个素数p，把p*i筛掉（p<=e[i]）

此时会检查i的最小素数因子是不是p

所以会有两种可能

1.i和p互素

Phi[i*p]=phi[i]*phi[p]

2.i的最小素因子刚好是p

Phi[i*p]=phi[i]*p

φ[i]=(p1-1)*p1^(q1-1)+(p2-1)*p2^(q2-1)......(pn-1)*pn^(qn-1)

对于莫比乌斯函数也是差不多

1. i和p互素  mul[i*p]=mul[i]*(-1)
2. i的最小素因子刚好是p  mul[i*p]=0

约数个数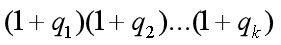

约数和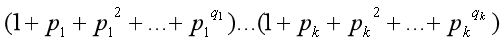

求f(n)=[n/1]+[n/2]+---+[n/n]的值

1. k<sqrt(n)的时候，k只有sqrt(n)种取值

　　所以n div k的取值最多只有sqrt(n)种

　　div是整除

　　2.k>sqrt(n)的时候

　　n div k 显然小于sqrt(n)

　　所以它的取值也只有sqrt(n)种

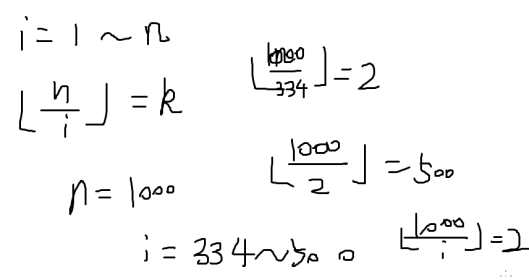
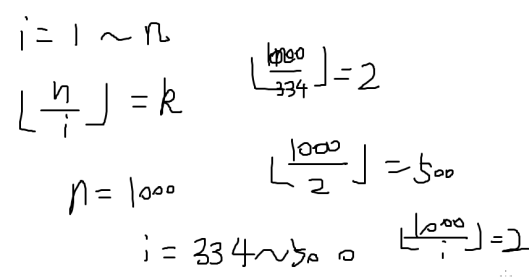
表面上复杂度是o(n)，但是由于我们是跳着走的，所以复杂度为o(2√n)