js 一道题目引发的正则的学习
正则表达式中的特殊字符
字符 含意
\ 做为转意,即通常在"\"后面的字符不按原来意义解释,如/b/匹配字符"b",当b前面加了反斜杆后/\b/,转意为匹配一个单词的边界。
-或-
对正则表达式功能字符的还原,如"*"匹配它前面元字符0次或多次,/a*/将匹配a,aa,aaa,加了"\"后,/a\*/将只匹配"a*"。 ^ 匹配一个输入或一行的开头,/^a/匹配"an A",而不匹配"An a"
$ 匹配一个输入或一行的结尾,/a$/匹配"An a",而不匹配"an A"
* 匹配前面元字符0次或多次,/ba*/将匹配b,ba,baa,baaa
+ 匹配前面元字符1次或多次,/ba*/将匹配ba,baa,baaa
? 匹配前面元字符0次或1次,/ba*/将匹配b,ba
(x) 匹配x保存x在名为$1...$9的变量中
x|y 匹配x或y
{n} 精确匹配n次
{n,} 匹配n次以上
{n,m} 匹配n-m次
[xyz] 字符集(character set),匹配这个集合中的任一一个字符(或元字符)
[^xyz] 不匹配这个集合中的任何一个字符
[\b] 匹配一个退格符
\b 匹配一个单词的边界
\B 匹配一个单词的非边界
\cX 这儿,X是一个控制符,/\cM/匹配Ctrl-M
\d 匹配一个字数字符,/\d/ = /[0-9]/
\D 匹配一个非字数字符,/\D/ = /[^0-9]/
\n 匹配一个换行符
\r 匹配一个回车符
\s 匹配一个空白字符,包括\n,\r,\f,\t,\v等
\S 匹配一个非空白字符,等于/[^\n\f\r\t\v]/
\t 匹配一个制表符
\v 匹配一个重直制表符
\w 匹配一个可以组成单词的字符(alphanumeric,这是我的意译,含数字),包括下划线,如[\w]匹配"$5.98"中的5,等于[a-zA-Z0-9]
\W 匹配一个不可以组成单词的字符,如[\W]匹配"$5.98"中的$,等于[^a-zA-Z0-9]。
1.regularexpression=/pattern/[switch] 关于正则后面的 switch: gi ,g ,i 的含义.
g: 全局匹配 i: 忽略大小写 gi: 全局匹配 + 忽略大小写
2.string.match() 和 RegExp.exec() 两个函数的区别
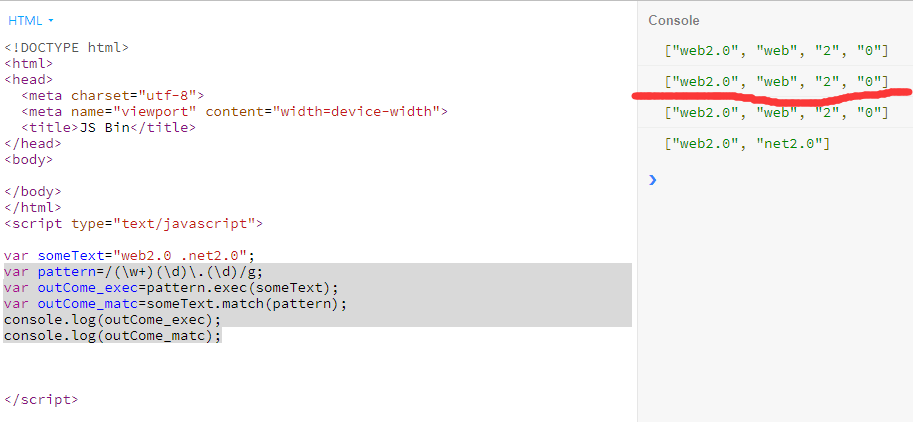
大都数情况下返回值是一样的 当pattern 后面的switch 为g 或者gi的时候 。
RegExp.exec() :返回的是第一个匹配的元素 加上所有括号内的元素(pattern中包含三个分组((\w+)、(\d)、(\d)))所以返回的数组为 : ["web2.0", "web", "2", "0"]。
string.match(): 这个方法规则是全局匹配,匹配所有符合规定规则的所有元素(并不显示pattern中包含的分组)。 所以返回的数组为 :["web2.0", "net2.0"]。
当pattern 后面的switch 为空的时候:
RegExp.exec() ,string.match() :返回的是第一个匹配的元素 加上所有括号内的元素(pattern中包含三个分组((\w+)、(\d)、(\d)))所以返回的数组为 : ["web2.0", "web", "2", "0"]。
看一下上面示例引申出的题目就很明显知道题目选项是 ?
What is outCome_exec[1] and outCome_matc[1]?
Choice A: true
Choice B: false
Choice C: null
Choice D: Web
Choice E: Web2.0
Choice F: undefined
Choice G: net2.0
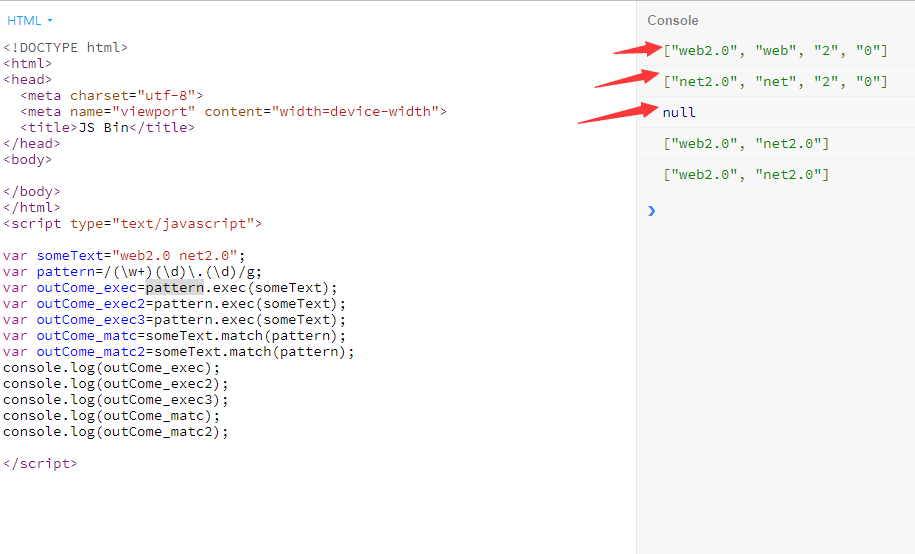
当pattern 后面的switch 为g 或者gi的时候:
RegExp.exec(): 多次执行时,首个匹配值也会随着执行次数+1(比如第二次执行会过滤掉第一个匹配到的元素,返回第二个匹配到的值)。当第n次执行后没有匹配值则返回null;
string.match():返回匹配所有符合规定规则的所有元素。(并不显示pattern中包含的分组)
3. RegExp.test( str )检查当前字符是否匹配正则表达式,返回值为Boolean。 test方法每次只查找最多一个匹配,如果找到立马返回true ,找不到返回false。如果regExpObject 带有全局标识g,当test方法多次执行时,首个匹配值也会随着执行次数+1(见上面exec示例)。
3.1 string.search() 检查当前字符串是否能匹配正则表达式-1表示不能匹配 0表示匹配。
4.和string.replace() 方法结合使用删除特定字符(去除空格):
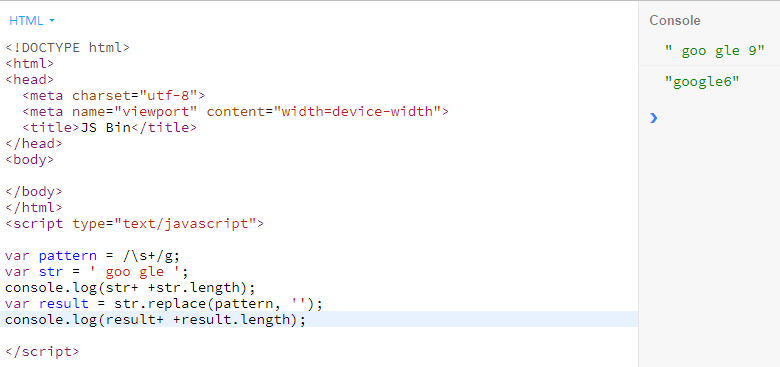
5.string.split()将字符串分割成数组
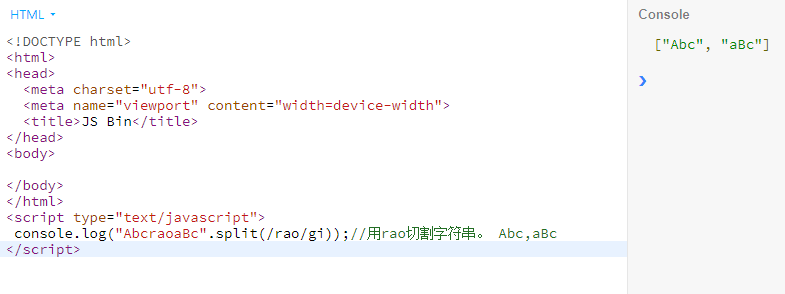
js 一道题目引发的正则的学习的更多相关文章
- L1-3 宇宙无敌加法器 - 令人激动的一道题目
L1-3 宇宙无敌加法器 - 令人激动的一道题目 感觉好久没有这么认真的做一道题了,今天看到一句话, 说是编程是一个工程型的工作,想要学好,"无他,唯手熟尔" 之前觉得自己笨,怀疑 ...
- 由SecureCRT引发的思考和学习
由SecureCRT引发的思考和学习 http://mp.weixin.qq.com/s?__biz=MzAxOTAzMDEwMA==&mid=2652500597&idx=1& ...
- 浅谈 js 字符串 trim 方法之正则篇
原文:浅谈 js 字符串 trim 方法之正则篇 关于 trim 其实没啥好说的,无非就是去除首位空格,对于现代浏览器来说只是简单的正则 /^\s+|\s+$/ 就可以搞定了.而且支持中文空格 等 ...
- js截取相应的域名----正则匹配法 和校验Url 正则表达式
js截取相应的域名----正则匹配法 和校验Url 正则表达式 用javascript截取相应的域名方法两种,供大家参考 1.方法1: [javascript] view plain copy fun ...
- JS稀奇古怪题目
JS稀奇古怪题目: 1.操作对象属性优先级高于普通赋值操作 var a = { n: 1 }; var b = a; //操作对象属性优先级高于普通赋值操作 a.x = a = { n: 2 }; c ...
- 一道原生js题目引发的思考(鼠标停留区块计时)
我瞎逛个啥论坛,发现了一个题目,于是本着练手的心态就开始写起来了,于是各种问题接踵而至,收获不小. 题目是这样的: Demo: mouseenter与mouseover区别demo 跨浏览器的区块计数 ...
- 一道codeforces题目引发的差分学习
Codeforces Round #688 (Div. 2) 题目:B. Suffix Operations 题意:给定一个长为n的数组a,你可以进行两种操作:1).后缀+1; 2)后缀-1: ...
- (转)js一道比较考验的题目
转载下别人曾经出过的一道面试题,此题是他出的一套前端面试题中的最后一题,用来考核面试者的JavaScript的综合能力,很可惜到目前为止的将近两年中,几乎没有人能够完全答对,并非多难只是因为大多面试者 ...
- 一道JS面试题引发的血案
刚入职新公司,属于公司萌新一枚,一天下午对着屏幕看代码架构时. BI项目组长给我看了一道面试别人的JS面试题. 虽然答对了,但把理由说错了,照样不及格. 话不多说,直接上题: var a = 1; s ...
随机推荐
- 关于tomcat NoClassDefDoundErr异常的记录
在做DRP项目的时候,copy了drp1.3,粘贴重命名成drp1.4,把drp1.4加入到tomcat中,发现drp1.4中新加的jsp可以正常运行,而从1.3那copy来的不能运行,抛出NoCla ...
- Python自动化学习--异常提示
举例:打开一个不存在的文件时: >>open("abc.txt","r")会提示错误 Traceback (most recent call las ...
- 小程序makePhoneCall拨打电话问题
调用wx.makePhoneCall后肯定会弹出一个询问框,此时无论是点击确认或者取消,页面都会依次触发app.js中的onHide函数和onShow函数,所以需要注意
- MYSQL数据导出与导入,secure_file_priv参数设置
https://www.imooc.com/article/41883 MySQL 报错 [Code: 1290, SQL State: HY000] The MySQL server is run ...
- canvas合并两张图片
解析: 原理是一样的 画多张图需要一张一张画 也就是等图片onload成功后处理 这里代码写的比较随意 实际用的时候可以小粉转一下 也非常简单.我懒~~ 么么.. newImage(text) { / ...
- layui问题之渲染数据表格时,只显示10条数据
通过ajax请求的数据,console.log()有30条数据,实际上只显示10条, 原因是没有设置limit table.render({ elem: '#report-collection' , ...
- 【leetcode】1175. Prime Arrangements
题目如下: Return the number of permutations of 1 to n so that prime numbers are at prime indices (1-inde ...
- logstash+redis收集负载均衡模式下多台服务器的多个web日志
一.logstash的简介 一般我们看日志来解决问题的时候要么 tail+grep 要么 把日志下载下来再搜索,可以应付不多的主机和应用不多的部署场景.但对于多机多应用部署就不合适了.这里的多机多应用 ...
- IO流,字节流复制文件,字符流+缓冲复制文件
JAVAIO如果按流向分:输入流和输出流两种 输入流的基类:InputStream Reader 输出流的基类:OutputStream Writer 如果按数据单元划分:字节流和字符流 字节 ...
- css常用小知识点汇总(一)
1.文本过多溢出,怎么让他隐藏变成点点点(...)呢? text-overflow:ellipsis;overflow:hidden;display:-webkit-box;-webkit-line- ...
