JavaScript求取水仙花数

一、什么是水仙花数

水仙花数也称为超完全数字不变数、自幂数、阿姆斯壮数、阿姆是特朗数。

水仙花数是指一个三位数，每个位数上数字的3次幂之和等于数字它本身。

水仙花数是自幂数的一种，三位的三次自幂数才叫做水仙花数；三位的水仙花数总够有4个：153,370,371,470

二、通过JS取得水仙花数

思路分析：

1、使用for循环查找遍历 从100到 999的所有三位数；

2、判断遍历的数字是否是各个位数的数字的3次幂数之和是否等于数字本身，如果是即为水仙花数，则在控制台输出（如何选取各个位数）

（1）选取个位数  模以10，得到余数即为个位数

（2）选取十位数  i除以10，再对结果进行取整，取整后得到一个两位数的整数。用这个结果对10取模，得到十位数

（3）选取百位数  三位数除以100，再取整，就得到了百位数。

3、使用 if语句 判断 i 是否是水仙花数。Math对象用于执行数学任务，pow(x , y)函数用于求取 x 的 y 次幂。

 for(var i = 100;i<=999;i++){
     var gw = i%10;
     var sw = parseInt(i/10) % 10;
     var bw = parseInt(i/100);
    if(i == Math.pow(gw,3)+Math.pow(sw,3)+Math.pow(bw,3)){
     console.log(i);
 }
 }

输出结果为：

三、求取其他的自幂数

• 一位自幂数：独身数
• 两位自幂数：没有
• 三位自幂数：水仙花数
• 四位自幂数：四叶玫瑰数
• 五位自幂数：五角星数
• 六位自幂数：六合数
• 七位自幂数：北斗七星数
• 八位自幂数：八仙数
• 九位自幂数：九九重阳数
• 十位自幂数：十全十美数

1、四叶玫瑰数 （1634,8208,9474）

 for(var i = 1000;i<=9999;i++){
     var gw = i%10;
     var sw = parseInt(i/10)%10;
     var bw = parseInt(i/100)%10;
     var qw = parseInt(i/1000);
 if(i == Math.pow(gw,4)+Math.pow(sw,4)+Math.pow(bw,4)+Math.pow(qw,4)){
     console.log(i);}
 }

2、五角星数 （54748, 92727,93084）

console.time('五角星数');
for(var i = 10000;i<=99999;i++){
    var gw = i%10;
    var sw = parseInt(i/10)%10;
    var bw = parseInt(i/100)%10;
    var qw = parseInt(i/1000)%10;
    var ww = parseInt(i/10000);
 if(i==Math.pow(gw,5)+Math.pow(sw,5)+Math.pow(bw,5)+Math.pow(qw,5)+Math.pow(ww,5)){
    console.log(i);}
}
console.timeEnd('五角星数');

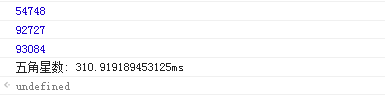
 注意：这里面使用 console.time() 和 console.timeEnd() 来计算 运行的时间

console.time() 方法是作为计算器的起始方法，该方法一般用于测试程序执行的时长。

console.timeEnd() 方法为计算器的结束方法，并将执行时长显示在控制台。

6、六合数（548834）

 console.time('六合数');
 for(var i = 100000;i<=999999;i++){
     var gw = i%10;
     var sw = parseInt(i/10)%10;
     var bw = parseInt(i/100)%10;
     var qw = parseInt(i/1000)%10;
     var ww = parseInt(i/10000)%10;
      var shw = parseInt(i/100000);
  if(i==Math.pow(gw,6)+Math.pow(sw,6)+Math.pow(bw,6)+Math.pow(qw,6)+Math.pow(ww,6)+Math.pow(shw,6)){
     console.log(i);}
 }
 console.timeEnd('六合数');

7、北斗七星数（1741725，4210818，9800817，9926315）

console.time('北斗七星数');
for(var i = 1000000;i<=9999999;i++){
    var gw = i%10;
    var sw = parseInt(i/10)%10;
    var bw = parseInt(i/100)%10;
    var qw = parseInt(i/1000)%10;
    var ww = parseInt(i/10000)%10;
     var sww = parseInt(i/100000)%10;
    var qww = parseInt(i/1000000);
 if(i==Math.pow(gw,7)+Math.pow(sw,7)+Math.pow(bw,7)+Math.pow(qw,7)+Math.pow(ww,7)+Math.pow(sww,7)+Math.pow(qww,7)){
    console.log(i);}
}
console.timeEnd('北斗七星数');

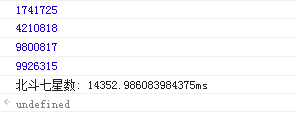
8、八仙数（24678050，24678051，8859347）

 console.time('八仙数');
 for(var i = 10000000;i<=99999999;i++){
     var gw = i%10;
     var sw = parseInt(i/10)%10;
     var bw = parseInt(i/100)%10;
     var qw = parseInt(i/1000)%10;
     var ww = parseInt(i/10000)%10;
      var sww = parseInt(i/100000)%10;
     var qww = parseInt(i/1000000)%10;
     var www = parseInt(i/10000000);
  if(i==Math.pow(gw,8)+Math.pow(sw,8)+Math.pow(bw,8)+Math.pow(qw,8)+Math.pow(ww,8)+Math.pow(sww,8)+Math.pow(qww,8)+Math.pow(www,8)){
     console.log(i);}
 }
 console.timeEnd('八仙数');

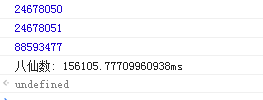
补充一些其他的Math对象：

• Math.pow(2,53) // => 9007199254740992:  2 的 53次幂
• Math.round(.6) // => 1.0:   四舍五入
• Math.ceil(.6) // => 1.0:   向上求整
• Math.floor(.6) // => 0.0:   向下求整
• Math.abs(-5)// => 5:   求绝对值
• Math.max(x,y,z)    返回最大值
• Math.min(x,y,z)   返回最小值
• Math.random()   生成一个大于等于0小于1.0的伪随机数
• Math.PI // π: 圆周率
• Math.E // e: 自然对数的底数
• Math.sqrt(3)   3的平方根
• Math.pow(3, 1/3)   3的立方根
• Math.sin(0)    三角函数: 还有Math.cos, Math.atan等
• Math.log(10)   10的自然对数
• Math.log(100)/Math.LN10   以10为底100的对数
• Math.log(512)/Math.LN2    以2为底512的对数
• Math.exp(3)   e的三次幂

通过JS来得到一系列的自幂数，是有一定的规律在里面的，有兴趣的话可以动手尝试一下，如果看了这篇博客能有所帮助的话，不胜荣幸~