Dockerfile+Jenkinsfile+GitLab轻松实现.NetCore程序的CI&CD

一.相关介绍

Dockerfile：关于Dockerfile的使用说明，我在文章《让.NetCore程序跑在任何有docker的地方》中有说到，这里不在赘述，需要的可以先看下，本文主要介绍Jenkinsfile结合dockerfile配合使用，自动构建.NetCore应用程序。

 

Jenkinsfile ：Jenkinsfile 是 Jenkins 2.x 或更高版本核心特性 Pipeline（流水线） 的脚本，或者说对于Jenkins 流水线的定义被写在一个叫Jenkinsfile的文本文件中，该文件可以被提交到项目的源代码的控制仓库。这是"流水线即代码"的基础; 将CD 流水线作为应用程序的一部分，像其他代码一样进行版本化和审查。 创建 `Jenkinsfile`并提交它到源代码控制中提供了以下几个好处:

• 自动地为所有分支创建流水线构建过程并拉取请求。
• 在流水线上代码复查/迭代 (以及剩余的源代码)。
• 对流水线进行审计跟踪。
• 该流水线的真正的源代码 , 可以被项目的多个成员查看和编辑。

Jenkinsfile 能使用两种语法进行编写，分别是“声明式”和“脚本化”，二者语法都是 DSL(Domain-specific language) 语言，二者语法差不多，下面我们具体看下

 

 

二.Jenkins和GitLab的安装

工欲善其事，必先利其器

Jenkins的安装可以看我之前的一篇文章：https://www.cnblogs.com/peyshine/p/12891935.html

Gitlab的安装推荐看下这篇文章：https://segmentfault.com/a/1190000021593151

 

三.打通GitLab Webhooks与Jenkins流程

1.这里先新建一个.net core应用程序，除了新增加了一个Jenkinsfile文件以外，其他没有任何代码的修改

注意，Jenkinsfile的J需要大写，我测试了，小写会提示找不到文件.

Jenkinsfile中添加了几行测试代码：

pipeline{
    agent any
    stages {
        stage('Build') {
            steps{
                echo 'This is a build step'
            }
        }
        stage('Test') {
            steps{
                echo 'This is a test step'
            }
        }
        stage('Deploy') {
            steps{
                echo 'This is a deploy step'
            }
        }
    }
}

然后将程序文件push到Gitlab上

 

2.在Jenkins系统管理，系统配置中，在Gitlab处添加相关信息

 

 

下面点击添加凭据，类型选择GitLab Api Token，由于这个Token需要由GitLab来提供，所以先到GitLab生成一个Api Token

 

3.生成Api Token

 

 

点击创建之后，Token就生效了

 

将Api Token复制到Jenkins中，点击添加

添加完成后，就可以在Credentials中选择刚刚添加好的凭据

点击保存，这样系统配置中的Gitlab的全局配置就生效了

 

4.新建流水线任务测试

下面打开Jenkins，新建一个流水线发布任务，取名test，然后点击确定.

勾选构建触发器

由于我们需要达到的目的是在GitLab提交代码，Jenkins可以自动构建相关任务，所以我们还需要配置一个触发器。如图，点击下面的"高级"按钮

点击“Generate”，生成一个SecretToken

然后再流水线Tab定义处，下拉选择“Pipeline script from SCM”，SCM选择Git，然后填写代码库的地址和访问用户密码，下面脚本路径有个Jenkinsfile，意思就是从我们提交到源代码管理根目录下面的Jenkinsfile中读取相关定义好的的流水线任务流程

点击保存

 

在Gitlab如下图地方进入，来配置web钩子

 

将在Jenkin中截图的一个url和生成的token分别填写在下方，在触发器的地方勾选上 Push events，然后点击下方的“Add webhook” 按钮。如果你还有其他事件发生时想触发Jenkins的任务，也可以自行勾选上

添加完成后点击测试

这个时候可以看到上方出现了成功的提示

而另一边Jenkins中，正在执行任务，并且任务的执行是 GitLab有推送任务

 完成之后，可以看到流水线任务流程图

下面通过代码推送来测一下，我在跟目录新建一个空的README.md文件，然后推送，推送完成后可以看到Jenkins开始执行第二次构建任务

至此，从GitLab提交代码到Jenkins自动构建的整个流程已经完成了，细心的你会发现，只是流程跑通了，这个Jenkinsfile没有实质性的内容，下面进入Jenkinsfile

 

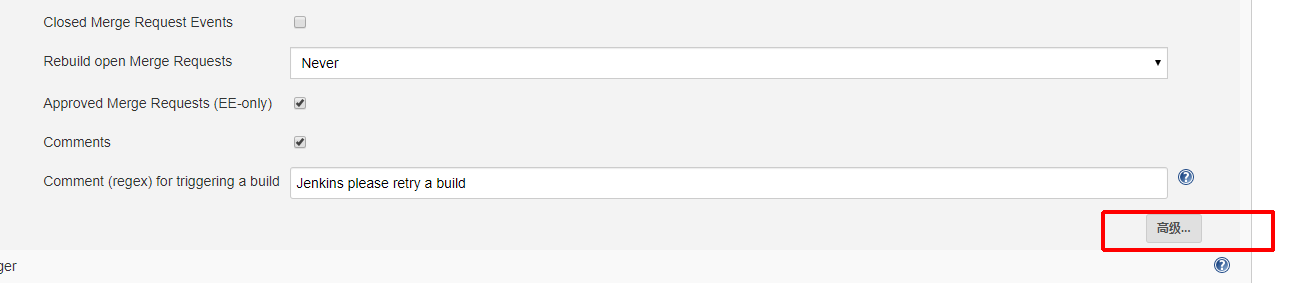
四.接入Jenkinsfile，Dockerfile实现自动发布

编写Dockerfile如下：

FROM mcr.microsoft.com/dotnet/core/sdk:3.1-buster AS build
COPY *.csproj ./app/
WORKDIR /app
RUN dotnet restore

COPY . ./
RUN dotnet publish -o out /p:PublishWithAspNetCoreTargetManifest="false"

FROM mcr.microsoft.com/dotnet/core/aspnet:3.1-buster-slim AS runtime
ENV ASPNETCORE_URLS http://+:80
WORKDIR /app
COPY --from=build /app/out ./
ENTRYPOINT ["dotnet", "WebApplication_Jenkinsfile.dll"]

 

编写Jenkinsfile如下：

pipeline{
    agent any
    stages {
        stage('Checkout') {
            steps{
            git credentialsId: '85ca7e47-532e-4901-9828-50a8da071d16', url: 'http://xxx.gitlab.com/webapplication_jenkinsfile.git', branch:'master'
                    echo '---This is a Checkout step---'
            }
        }
        stage('Build') {
            steps{
                    sh '''cd WebApplication_Jenkinsfile
            docker rmi -f docker_webapplication_test:1.0
            docker build -t docker_webapplication_test:1.0 .'''
            echo '---This is a Build step---'
            }
        }
        stage('Run') {
            steps{
            sh '''docker rm -f docker_webapplication_test
            docker run --name docker_webapplication_test -d -p : docker_webapplication_test:1.0
            '''
                    echo '---This is a run step---'
            }
        }
    }
}

说明:

stages 必须，包括顺序执行的一个或多个stage命令，在pipeline内仅能使用一次，通常位于agent/options后面

steps 必须，steps位于stage指令块内部，包括一个或多个step。仅有一个step的情况下可以忽略关键字step及其{}

这里为了演示，只添加了几个核心的步骤，可以根据需要自行添加自动测试，邮件提醒等额外步骤

 

流水线语法，可以参照下图中的示例步骤点击后，可以生成脚本信息，上面Jenkinsfile中的git credentialsId信息就是在这里生成的

 

完成之后，将Jenkinsfile和Dockerfile推送到Gitlab，推送成功可以看到如下图的Jenkins自动构建过程，并且遵照定义规范发布了应用

 

 

如果需要查看日志，或者在发布失败后查看失败原因，可以通过下面的 Console Output来查看

Console Output中的详细日志信息如下图，可以看到构建过程是遵循在Dockerfile中的定义

docker 容器运行状态检查

自动部署效果截图

五.结束总结

在定义web钩子的时候，我勾选的是push events，所以每次有提交代码到master，都会自动去走Jenkinsfile中的流水线任务，在实际生产中，如果不想这样操作，可以将持续集成流水线与持续发布流水线独立开来

其实只需要前期一次将Jenkins和Gitlab触发器打通之后，后面只需要在源代码中维护Dockerfile和Jenkinsfile即可，这是比较优雅的一种CI、CD方式，动手试试吧！