UVA - 10689 Yet another Number Sequence （矩阵快速幂求斐波那契）

题意：已知f(0) = a，f(1) = b，f(n) = f(n − 1) + f(n − 2), n > 1，求f(n)的后m位数。

分析：n最大为10⁹，矩阵快速幂求解，复杂度log2(10⁹)。

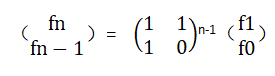
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<cmath>
#include<iostream>
#include<sstream>
#include<iterator>
#include<algorithm>
#include<string>
#include<vector>
#include<set>
#include<map>
#include<stack>
#include<deque>
#include<queue>
#include<list>
#define lowbit(x) (x & (-x))
const double eps = 1e-9;
inline int dcmp(double a, double b){
    if(fabs(a - b) < eps) return 0;
    return a > b ? 1 : -1;
}
typedef long long LL;
typedef unsigned long long ULL;
const int INT_INF = 0x3f3f3f3f;
const int INT_M_INF = 0x7f7f7f7f;
const LL LL_INF = 0x3f3f3f3f3f3f3f3f;
const LL LL_M_INF = 0x7f7f7f7f7f7f7f7f;
const int dr[] = {0, 0, -1, 1, -1, -1, 1, 1};
const int dc[] = {-1, 1, 0, 0, -1, 1, -1, 1};
const int MOD = 1000007;
const double pi = acos(-1.0);
const int MAXN = 400 + 10;
const int MAXT = 1000 + 10;
using namespace std;
int POW[10];
int a, b, n, m;
void init(){
    POW[1] = 10;
    for(int i = 2; i <= 4; ++i){
        POW[i] = POW[i - 1] * 10;
    }
}
struct Matrix{
    int r, c;
    int matrix[2][2];
    Matrix(int rr, int cc):r(rr), c(cc){
        memset(matrix, 0, sizeof matrix);
    }
};
Matrix mul(Matrix a, Matrix b){
    Matrix ans(a.r, b.c);
    for(int i = 0; i < a.r; ++i){
        for(int j = 0; j < b.c; ++j){
            int tmp = 0;
            for(int k = 0; k < a.c; ++k){
                (tmp += a.matrix[i][k] * b.matrix[k][j]) %= POW[m];
            }
            ans.matrix[i][j] = tmp;
        }
    }
    return ans;
}
Matrix QPOW(Matrix tmp, int k){
    Matrix ans(2, 2);
    ans.matrix[0][0] = ans.matrix[1][1] = 1;
    while(k){
        if(k & 1) ans = mul(ans, tmp);
        tmp = mul(tmp, tmp);
        k >>= 1;
    }
    return ans;
}
int main(){
    int T;
    scanf("%d", &T);
    init();
    while(T--){
        scanf("%d%d%d%d", &a, &b, &n, &m);
        Matrix tmp1(2, 2), tmp2(2, 1);
        tmp1.matrix[0][0] = tmp1.matrix[0][1] = tmp1.matrix[1][0] = 1;
        tmp2.matrix[0][0] = b;
        tmp2.matrix[1][0] = a;
        Matrix ans = mul(QPOW(tmp1, n - 1), tmp2);
        printf("%d\n", ans.matrix[0][0]);
    }
    return 0;
}