C++堆排序算法的实现

堆排序（Heap　sort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以用到上一次的排序结果，所以不像其他一般的排序方法一样，每次都要进行n-1次的比较，复杂度为O(nlogn)。

这里先说明以下几个基本概念：

完全二叉树：假设一个二叉树有n层，那么如果第1到n-1层的每个节点都达到最大的个数：2，且第n层的排列是从左往右依次排开的，那么就称其为完全二叉树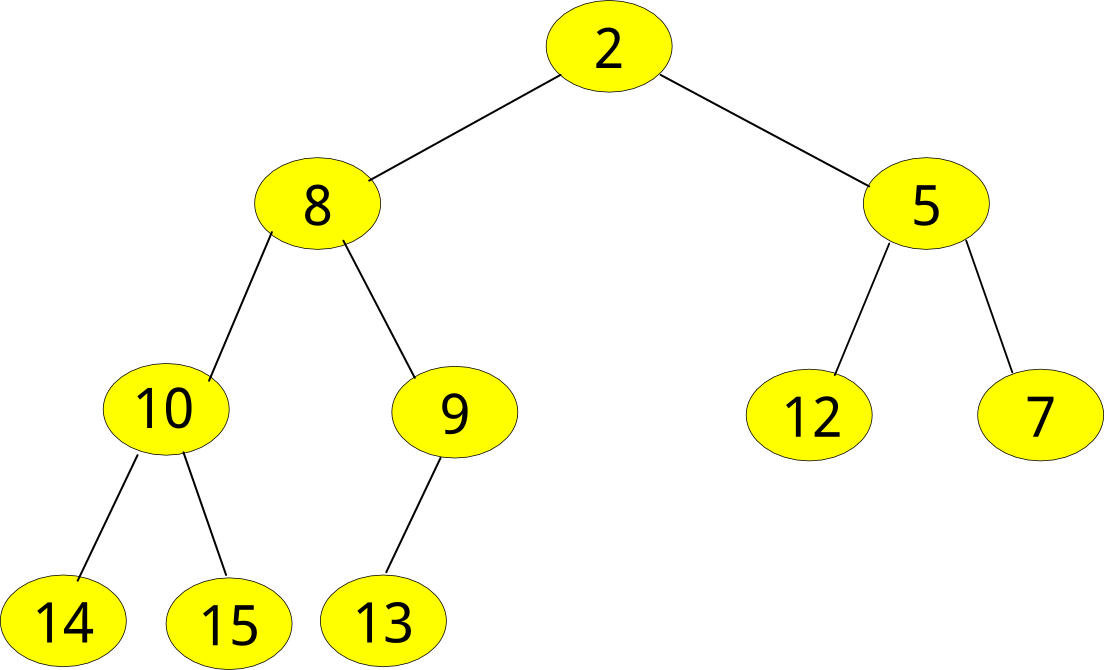

堆：本身就是一个完全二叉树，但是需要满足一定条件，当二叉树的每个节点都大于等于它的子节点的时候，称为大顶堆，当二叉树的每个节点都小于它的子节点的时候，称为小顶堆，上图即为小顶堆。

关键的性质：

将堆的内容填入一个一维数组，这样通过下标就能计算出每个结点的父子节点，编号顺序从0开始，从左往右，从上至下层次遍历。a[10] = {2,8,5,10,9,12,7,14,15,13}

若一个结点的下标为k，那么它的父结点为(k-1)/2，其子节点为2k+1和2k+2

例：数字为10的节点的下标为3，父结点为1号：8，子节点为7号和8号：14，15

算法步骤：

1）利用给定数组创建一个堆H[0..n-1]（我们这里使用最小堆），输出堆顶元素

2）以最后一个元素代替堆顶，调整成堆，输出堆顶元素

3）把堆的尺寸缩小1

4） 重复步骤2，直到堆的尺寸为1

实现代码：

#include <iostream>
#include <vector>
#include <algorithm>
#include <time.h>
#include <Windows.h>
using namespace std;//堆排序的核心是建堆,传入参数为数组，根节点位置，数组长度
void Heap_build(int a[],int root,int length)
{
    int lchild = root*+;//根节点的左子结点下标
    if (lchild < length)//左子结点下标不能超出数组的长度
    {
        int flag = lchild;//flag保存左右节点中最大值的下标
        int rchild = lchild+;//根节点的右子结点下标
        if (rchild < length)//右子结点下标不能超出数组的长度(如果有的话)
        {
            if (a[rchild] > a[flag])//找出左右子结点中的最大值
            {
                flag = rchild;
            }
        }
        if (a[root] < a[flag])
        {
            //交换父结点和比父结点大的最大子节点
            swap(a[root],a[flag]);
            //从此次最大子节点的那个位置开始递归建堆
            Heap_build(a,flag,length);
        }
    }
}

void Heap_sort(int a[],int len)
{
    for (int i = len/; i >= ; --i)//从最后一个非叶子节点的父结点开始建堆
    {
        Heap_build(a,i,len);
    }

    for (int j = len-; j > ; --j)//j表示数组此时的长度，因为len长度已经建过了，从len-1开始
    {
        swap(a[],a[j]);//交换首尾元素,将最大值交换到数组的最后位置保存
        Heap_build(a,,j);//去除最后位置的元素重新建堆，此处j表示数组的长度，最后一个位置下标变为len-2
    }

}
int main(int argc, char **argv)
{
    clock_t Start_time = clock();
    int a[] = {,,,,,,,,,};
    Heap_sort(a,);
     for (size_t i = ; i != ; ++i)
     {
         cout<<a[i]<<" ";
     }
    clock_t End_time = clock();
    cout<<endl;
    cout<<"Total running time is: "<<static_cast<double>(End_time-Start_time)/CLOCKS_PER_SEC*<<" ms"<<endl;
    cin.get();
    return ;
}

建堆的过程，堆调整的过程，这些过程的时间复杂度，空间复杂度，以及如何应用在海量数据Top K问题中等等，都是需要重点掌握的。

复杂度分析：
最差时间复杂度O(n log n)
最优时间复杂度O(n log n)
平均时间复杂度O(n log n)
最差空间复杂度O(n)

注意：此排序方法不适用于个数少的序列，因为初始构建堆需要时间；

特点分析：不稳定算法(unstable sort)、In-place sort。

---------------------

转载：

作者：MISAYAONE
来源：CSDN
原文：https://blog.csdn.net/misayaaaaa/article/details/65999854
版权声明：本文为博主原创文章，转载请附上博文链接！

有问题欢迎一起讨论！