SOSdp

---

layout: post

title: SOSdp

author: "luowentaoaa"

catalog: true

tags:

mathjax: true

- codeforces

- DP

---

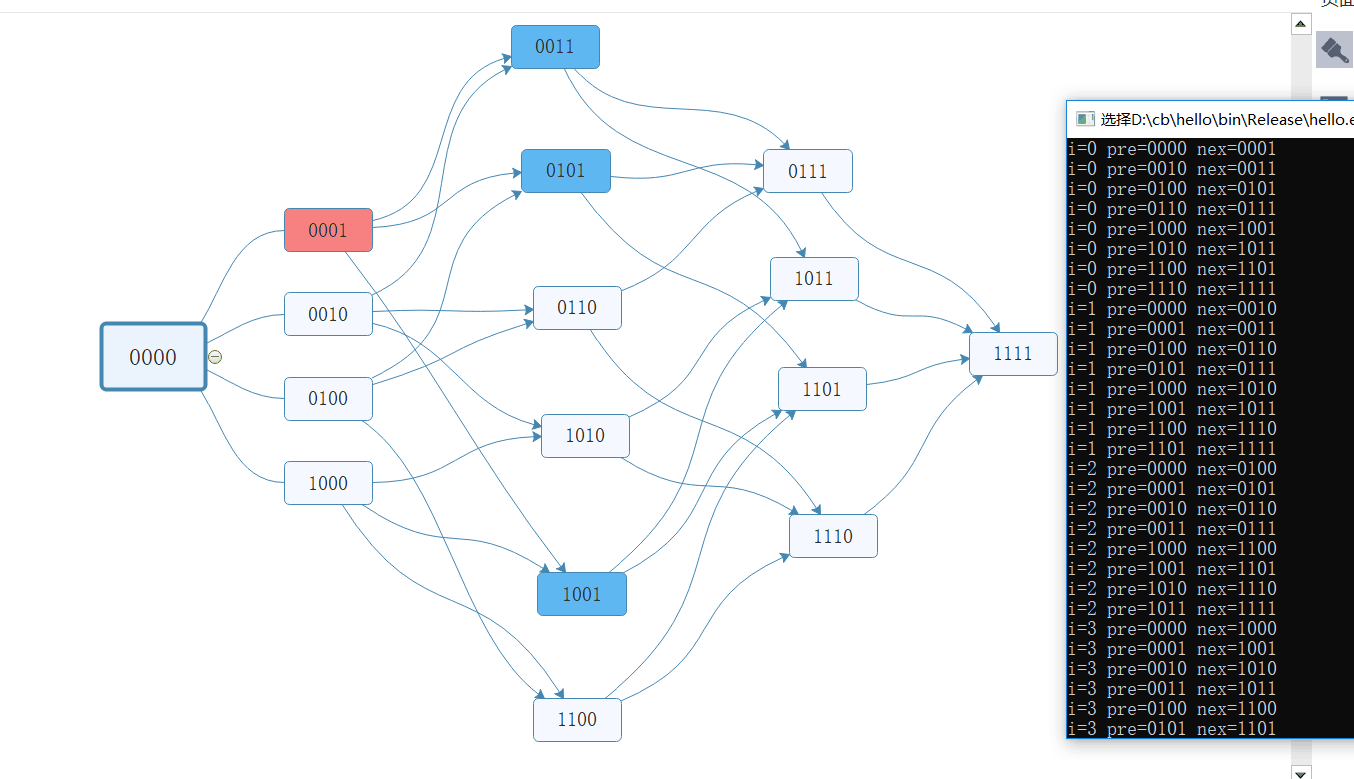
i=0 pre=0000 nex=0001
i=0 pre=0010 nex=0011
i=0 pre=0100 nex=0101
i=0 pre=0110 nex=0111
i=0 pre=1000 nex=1001
i=0 pre=1010 nex=1011
i=0 pre=1100 nex=1101
i=0 pre=1110 nex=1111
i=1 pre=0000 nex=0010
i=1 pre=0001 nex=0011
i=1 pre=0100 nex=0110
i=1 pre=0101 nex=0111
i=1 pre=1000 nex=1010
i=1 pre=1001 nex=1011
i=1 pre=1100 nex=1110
i=1 pre=1101 nex=1111
i=2 pre=0000 nex=0100
i=2 pre=0001 nex=0101
i=2 pre=0010 nex=0110
i=2 pre=0011 nex=0111
i=2 pre=1000 nex=1100
i=2 pre=1001 nex=1101
i=2 pre=1010 nex=1110
i=2 pre=1011 nex=1111
i=3 pre=0000 nex=1000
i=3 pre=0001 nex=1001
i=3 pre=0010 nex=1010
i=3 pre=0011 nex=1011
i=3 pre=0100 nex=1100
i=3 pre=0101 nex=1101
i=3 pre=0110 nex=1110
i=3 pre=0111 nex=1111
i=0000
i=0001 0000
i=0010 0000
i=0011 0010 0001
i=0100 0000
i=0101 0100 0001
i=0110 0100 0010
i=0111 0110 0101 0011
i=1000 0000
i=1001 1000 0001
i=1010 1000 0010
i=1011 1010 1001 0011
i=1100 1000 0100
i=1101 1100 1001 0101
i=1110 1100 1010 0110
i=1111 1110 1101 1011 0111

Process returned 0 (0x0)   execution time : 0.067 s
Press any key to continue.

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+50;
typedef long long ll;
const ll mod=1e9+7;

char s[maxn];
int dp[(1<<21)+50];
bool ok[(1<<21)+50];
int cal(int x){
    if(x==0)return 0;
    return x%2+cal(x/2);
}
vector<int>v[maxn];

int main(){
    std::ios::sync_with_stdio(false);
    for(int i=0;i<4;i++){
        for(int j=0;j<(1<<4);j++){
            if((j&(1<<i))==0){
                bitset<4> a(j);
                cout<<"i="<<i<<" pre="<<a<<" nex=";
                a.set(i);
                cout<<a.set(i)<<endl;
                v[j|(1<<i)].push_back(j);
                dp[j|(1<<i)]=max(dp[j|(1<<i)],dp[j]);
            }
        }
    }
    for(int i=0;i<(1<<4);i++){
        bitset<4> a(i);
        cout<<"i="<<a<<" ";
        for(auto j:v[i]){
            bitset<4> b(j);
            cout<<b<<" ";
        }
        cout<<endl;
    }
    return 0;
}