Gluon学习02-使用GPU

小书匠kindle

目录,方便快速定位:

• 1.安装cuda与cudnn
• 2.安装mxnet-gpu

---

本机环境介绍:

系统:Linuxmint

Python版本:Python3

1.安装cuda与cudnn

(0)定义

CUDA(Compute Unified Device Architecture)，是英伟达公司推出的一种基于新的并行编程模型和指令集架构的通用计算架构，它能利用英伟达GPU的并行计算引擎，比CPU更高效的解决许多复杂计算任务。

摘自:CPU、GPU、CUDA，CuDNN 简介

cuDNN（CUDA Deep Neural Network library）：是NVIDIA打造的针对深度神经网络的加速库，是一个用于深层神经网络的GPU加速库。如果你要用GPU训练模型，cuDNN不是必须的，但是一般会采用这个加速库。

摘自:GPU，CUDA，cuDNN的理解

(1)下载

选择合适版本下载cuda:

网址:https://developer.nvidia.com/cuda-downloads

选择合适版本

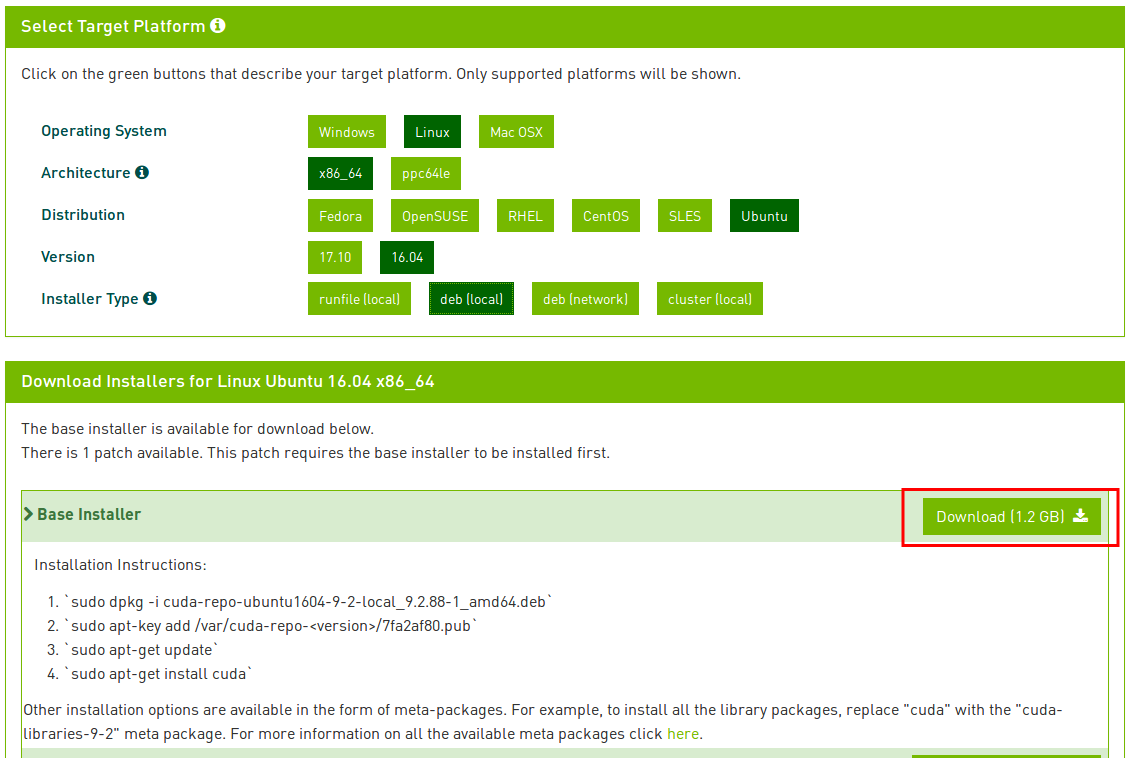
配合前面的cuda版本,下载相应的cudnn:

网址:https://developer.nvidia.com/rdp/cudnn-archive

注:这里需要注册账号才可以下,有时收不到激活邮件,可以多试试不同放入邮箱,不行就出去一下.

(2)安装

下载完成以上两个文件后,首先安装cuda,使用以下命令安装:

1. sudo dpkg -i cuda-repo-ubuntu1604-9-0-local_9.0.176-1_amd64.deb 
   

   ---

2. sudo apt-key add /var/cuda-repo-9-0-local/7fa2af80.pub 
   

   ---

3. sudo apt-get update 
   

   ---

4. sudo apt-get install cuda 
   

   ---

然后,解压cudnn,将相应文件拷贝的cuda的安装目录上,使用以下命令:

1. tar xvzf cudnn-8.0-linux-x64-v5.1-ga.tgz  
   

   ---

2. sudo cp cuda/include/cudnn.h /usr/local/cuda/include 
   

   ---

3. sudo cp cuda/lib64/libcudnn* /usr/local/cuda/lib64 
   

   ---

4. sudo chmod a+r /usr/local/cuda/include/cudnn.h /usr/local/cuda/lib64/libcudnn* 
   

   ---

(3)配置

将cuda安装路径配置到系统路径下:

1. export LD_LIBRARY_PATH="$LD_LIBRARY_PATH:/usr/local/cuda/lib64:/usr/local/cuda/extras/CUPTI/lib64" 
   

   ---

2. export CUDA_HOME=/usr/local/cuda 
   

   ---

根据自己环境将该信息添加到相应文件,我的是~/.zshrc,如果终端是bash,则是~/.bashrc.

2.安装mxnet-gpu

(1)卸载以前安装的CPU版本的mxnet

1. pip uninstall mxnet 
   

   ---

(2)安装mxnet-gpu

根据前面安装的cuda 版本,安装相应的mxnet-gpu

1. pip install --pre mxnet-cu75 # CUDA 7.5 
   

   ---

2. pip install --pre mxnet-cu80 # CUDA 8.0 
   

   ---

3. pip install --pre mxnet-cu90 # CUDA 9.0 
   

   ---

注:如果安装过程过慢,可以更换pip的源,更换方法是可以看这篇博客更换pip源到国内镜像

参考:

Gluon动手学深度学习

每日一学,争取进步02