Noip2003 提高组 神经网络

神经网络

题目背景

人工神经网络（Artificial Neural Network）是一种新兴的具有自我学习能力的计算系统，在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究一直是当今的热门方向，兰兰同学在自学了一本神经网络的入门书籍后，提出了一个简化模型，他希望你能帮助他用程序检验这个神经网络模型的实用性。

题目描述

在兰兰的模型中，神经网络就是一张有向图，图中的节点称为神经元，而且两个神经元之间至多有一条边相连，下图是一个神经元的例子：

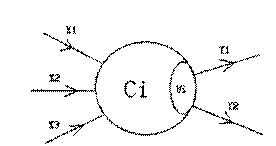
神经元〔编号为1）

图中，X1―X3是信息输入渠道，Y1－Y2是信息输出渠道，C1表示神经元目前的状态，Ui是阈值，可视为神经元的一个内在参数。

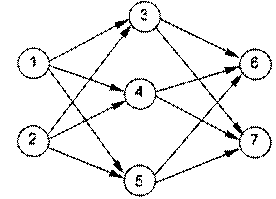
神经元按一定的顺序排列，构成整个神经网络。在兰兰的模型之中，神经网络中的神经无分为几层；称为输入层、输出层，和若干个中间层。每层神经元只向下一层的神经元输出信息，只从上一层神经元接受信息。下图是一个简单的三层神经网络的例子。

兰兰规定，Ci服从公式：（其中n是网络中所有神经元的数目）

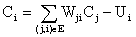
公式中的Wji（可能为负值）表示连接j号神经元和 i号神经元的边的权值。当 Ci大于0时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒它会向其他神经元传送信号，信号的强度为Ci。

如此．在输入层神经元被激发之后，整个网络系统就在信息传输的推动下进行运作。现在，给定一个神经网络，及当前输入层神经元的状态（Ci），要求你的程序运算出最后网络输出层的状态。

输入输出格式

输入格式：

输入文件第一行是两个整数n（1≤n≤100）和p。接下来n行，每行两个整数，第i＋1行是神经元i最初状态和其阈值（Ui），非输入层的神经元开始时状态必然为0。再下面P行，每行由两个整数i，j及一个整数Wij，表示连接神经元i、j的边权值为Wij。

输出格式：

输出文件包含若干行，每行有两个整数，分别对应一个神经元的编号，及其最后的状态，两个整数间以空格分隔。仅输出最后状态大于零的输出层神经元状态，并且按照编号由小到大顺序输出！

若输出层的神经元最后状态均为 0，则输出 NULL。

输入输出样例

输入样例#1：

5 6
1 0
1 0
0 1
0 1
0 1
1 3 1
1 4 1
1 5 1
2 3 1
2 4 1
2 5 1

输出样例#1：

3 1
4 1
5 1

思路:

　　拓扑排序

坑点:

　　①如果是输入、输出层，均不需要减去ui

　　②最后输出的是输出层，即出度为0的点

上代码:

#include <iostream>
#include <cstdio>
using namespace std;

const int M = ;
int n,p;
int a[M],b[M],ru[M],chu[M];
bool flag,vis[M];

struct node {
    int next,to,w;
}e[M<<];
int top,head[M];
void add(int u,int v,int w) {
    top++;
    e[top].to=v;
    e[top].w=w;
    e[top].next=head[u];
    head[u]=top;
}

void dfs(int u) {
    for(int i=head[u],v,w; i; i=e[i].next) {
        v=e[i].to,w=e[i].w;
        a[v]+=w*a[u];
        ru[v]--;
        if(!ru[v] && a[v]-b[v]>) a[v]-=b[v],dfs(v);
    }
}

int main() {
    scanf("%d%d",&n,&p);
    for(int i=,x; i<=n; i++) {
        scanf("%d%d",&a[i],&b[i]);
        if(a[i]>) vis[i]=true;
    }
    for(int i=,u,v,w; i<=p; i++) {
        scanf("%d%d%d",&u,&v,&w);
        add(u,v,w);
        ru[v]++;
        chu[u]++;
    }
    for(int i=; i<=n; i++)
        if(vis[i])
            dfs(i);
    for(int i=; i<=n; i++)
        if(chu[i]== && a[i]>) {
            printf("%d %d\n",i,a[i]);
            flag=true;
        }
    if(!flag) printf("NULL");
    return ;
}