BZOJ 3224 Tyvj 1728 普通平衡树 | Splay 板子+SPlay详细讲解

下面给出Splay的实现方法(复杂度证明什么的知道是 nlogn 就可以啦)

首先对于一颗可爱的二叉查找树,是不能保证最坏nlogn的复杂度(可以想象把一个升序序列插入)

(二叉查找树保证左子树元素大小都小于根元素大小,根元素大小都小于右子树元素大小,且子树都是二叉查找树)

所以我们需要一些非常巧妙的旋转操作 (ratate)来优化这棵树(并让他改名叫Splay)

(图片顺序全反了2333)

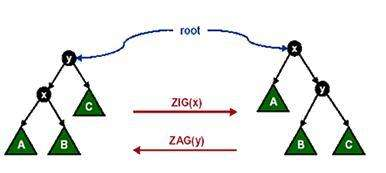
1.节点 x 的父节点 y 是根节点。这时，如果 x 是 y 的左孩子，我们进行一次 Zig （右旋）操作；如果 x 是 y 的右孩子，则我们进行一次 Zag（左旋）操作。经过旋转，x 成 为二叉查找树 S 的根节点，调整结束。

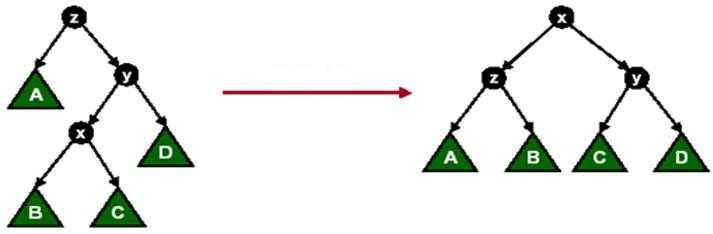
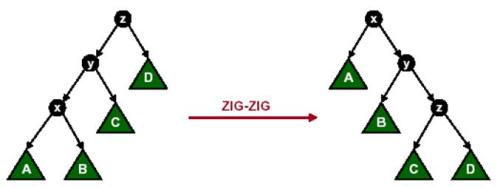
2.节点x 的父节点y 不是根节点，y 的父节点为z，且x 与y 同时是各自父节点 的左孩子或者同时是各自父节点的右孩子。这时，我们进行一次Zig-Zig操作或者Zag-Zag操作。

3.节点x的父节点y不是根节点，y的父节点为z，x与y中一个是其父节点的左孩子 而另一个是其父节点的右孩子。这时，我们进行一次Zig-Zag操作或者Zag-Zig 操作

在这个过程中我们完成了让x上移为的操作

假设我们已经领悟了这些操作,我们再学习一个Splay(x)函数让他不断调用Rotate,将x节点旋转到根节点,这样就完成了对SPlay的维护(实现比较简单,可以看代码)

非常重要的性质是,Rotate和Splay函数使得维护Splay树的时候无论以哪个节点为根,这棵树都是比较"优美"的(长得比较均匀)

下面着重讨论一下splay上的各种操作:

1.Find()

这个比较简单,我们只需要不断比较然后去左儿子或者右儿子即可

2.Insert()

先去Splay里面找x,如果找到了的话直接x计数器++,没找到就新建一个节点

我们只要重点考虑一下怎么维护这棵树的其他性质(例如子树大小)

回到刚刚的Splay()操作,我们可以发现,每次旋转之后旋转的节点的子树大小是可更新的,且不受到之后的影响(具体可画图理解)

所以我们可以把这个节点(新建的或者以前的)直接Splay到根节点就完成了维护

3.Getmax/min

额...直接不停往左或者往右即可

4.Earse

先考虑删除根节点(因为其他节点都是能移到根节点的)根节点的删除对子树信息没影响,所以可以直接删

然后现在剩下了两棵小树,我们只需要让一棵树接到另一棵树上即可,而这等价于让一棵树根节点的一个儿子为空

我们可以把左子树的最大儿子转到根,这样左子树的右儿子就是空的了,把右子树根节点接过去即可

5.getkth

利用计数器往左往右查找即可

6.getrank

这个别想得太复杂,直接把他转到根节点,左子树大小+1就是排名

7.getpre/nxt(找前驱后继)

转到根节点,然后直接找左子树最大值(右子树最小值)

讲到这里基本操作就OK啦,看看代码就学会了SPlay!

---

 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 #define N 100010
 #define which(x) (ls[fa[(x)]]==(x))
 typedef long long ll;
 using namespace std;
 int n,root,idx,val[N],fa[N],ls[N],rs[N],sze[N],cnt[N];
 int read()
 {
     int ret=,neg=;
     char j=getchar();
     for (;j>'' || j<'';j=getchar())
     if (j=='-') neg=-;
     for (;j>='' && j<='';j=getchar())
     ret=ret*+j-'';
     return ret*neg;
 }
 void upt(int x)//更新子树大小
 {
     sze[x]=sze[ls[x]]+sze[rs[x]]+cnt[x];
 }
 void rotate(int x)//旋转操作
 {
     //y是x父亲,z是y父亲,b是y的另一个儿子
     int y=fa[x],z=fa[y],b=which(x)?rs[x]:ls[x],dir=which(y);
     which(x)?(rs[x]=y,ls[y]=b):(ls[x]=y,rs[y]=b);
     fa[y]=x,fa[b]=y,fa[x]=z;
     if (z) dir?ls[z]=x:rs[z]=x;
     upt(y),upt(x);//更新大小
 }
 void splay(int x)//把x旋转至根节点
 {
     //为了让树平衡,如果x和父亲同向,转fa[x]染红转x
     //否则转两次x
     while (fa[x])
     {
     if (fa[fa[x]])
         if (which(x)==which(fa[x])) rotate(fa[x]);
         else rotate(x);
     rotate(x);
     }
     root=x;//现在x是根了
 }
 int getmin(int x)//找以x为根子树最小值节点编号
 {
     while (ls[x]) x=ls[x];
     return x;
 }
 int getmax(int x)//找以x为根子树最大值节点编号
 {
     while (rs[x]) x=rs[x];
     return x;
 }
 int find(int x)//找值为x的节点没有则返回
 {
     int cur=root,last=;
     while (cur && val[cur]!=x)
     {
     last=cur;
     if (x<val[cur]) cur=ls[cur];
     else cur=rs[cur];
     }
     return cur?cur:last;
 }
 void insert(int x)//插入x
 {
     int cur=find(x);//找到
     //如果已经存在x,把x++后splay成根节点
     if (cur && val[cur]==x) return (void)(cnt[cur]++,sze[cur]++,splay(cur));
     //如果不存在x就创造一个,然后splay
     val[++idx]=x,fa[idx]=cur,cnt[idx]=sze[idx]=;
     if (cur) x<val[cur]?ls[cur]=idx:rs[cur]=idx;
     splay(idx);
 }
 void erase(int x)//删除值为x的节点
 {
     int cur=find(x);//保证存在
     splay(cur);//先把x转到根
     //如果x个数大于1,直接删掉就好
     if (cnt[cur]>) cnt[cur]--,sze[cur]--;
     //如果有一个儿子节点为空,直接让另一个为根,如果都是空就说明树为空
     else if (!ls[cur] || !rs[cur]) root=ls[cur]+rs[cur],fa[root]=;
     else
     {
     fa[ls[cur]]=;//x的左儿子没爸爸了
     int u=getmax(ls[cur]);//让左子树最大值节点当新根节点,右子树的根节点是新根节点的右儿子
     splay(u);
     rs[u]=rs[cur],fa[rs[cur]]=u;
     upt(u);
     }
 }
 int getkth(int k)//寻找第k大,比较easy
 {
     int cur=root;
     while (cur)
     {
     if (sze[ls[cur]]>=k) cur=ls[cur];
     else if (sze[ls[cur]]+cnt[cur]>=k) return val[cur];
     else k-=sze[ls[cur]]+cnt[cur],cur=rs[cur];
     }
     return val[cur];
 }
 int getrank(int x)//询问x排名
 {
     int cur=find(x);
     splay(cur);
     return sze[ls[cur]]+;
 }
 int getpre(int x)//找前驱
 {
     int cur=find(x);
     if (val[cur]<x) return val[cur];
     splay(cur);
     return val[getmax(ls[cur])];
 }
 int getnxt(int x)//找后继
 {
     int cur=find(x);
     if (val[cur]>x) return val[cur];
     splay(cur);
     return val[getmin(rs[cur])];
 }
 int main()
 {
     n=read();
     for (int i=,op,x;i<=n;i++)
     {
     op=read(),x=read();
     if (op==) insert(x);
     if (op==) erase(x);
     if (op==) printf("%d\n",getrank(x));
     if (op==) printf("%d\n",getkth(x));
     if (op==) printf("%d\n",getpre(x));
     if (op==) printf("%d\n",getnxt(x));
     }
     return ;
 }