HDU 2855 斐波那契+矩阵快速幂

http://acm.hdu.edu.cn/showproblem.php?pid=2855

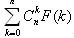化简这个公式，多写出几组就会发现规律

d[n]=F[2*n]

后面的任务就是矩阵快速幂拍一个斐波那契模板出来了

这里用的是2维 vector

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
typedef vector<int>vec;
typedef vector<vec>mat;
typedef long long ll;
typedef unsigned int uint;
int M;
mat mul(mat &a,mat &b)
{
    mat c(a.size(),vec(b[].size()));
    for(uint i=;i<a.size();i++)
    {
        for(uint k=;k<b.size();k++)
        {
            for(uint j=;j<b[].size();j++)
            {
                c[i][j]=(c[i][j]+a[i][k]*b[k][j])%M;
            }
        }
    }
    return c;
}

mat pow(mat a,ll n)
{
    mat b(a.size(),vec(a.size()));
    for(uint i=;i<a.size();i++)
    {
        b[i][i]=;
    }
    while(n>)
    {
        if(n&) b=mul(b,a);
        a=mul(a,a);
        n>>=;
    }
    return b;
}
ll n;
int main()
{
    int T,n,i;
    scanf("%d",&T);
    for(i=;i<=T;i++)
    {
        scanf("%d%d",&n,&M);
        mat a(,vec());
        a[][]=a[][]=a[][]=;
        a[][]=;
        a=pow(a,*n);
        printf("%d\n",a[][]);
    }
    return ;
}