POJ 3384 Feng Shui --直线切平面

题意：房间是一个凸多边形，要在里面铺设两条半径为r的圆形地毯，可以重叠，现在要求分别铺设到哪，使地毯所占的地面面积最大。

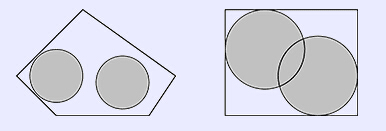
解法：要使圆形地毯所占面积最大，圆形地毯一定是与边相切的，这样才能使尽量不重叠。 那么我们把所有边都向内推进r，那么形成的多边形，可知两个圆形地毯的中心就一定在这个多边形边界上，最优的情况下是在此新凸包的最远点对上。

初始多边形为(-1000,-1000)到(1000,1000)的矩形，那么我们可以模拟把每条边都推进，每次切出新的凸多边形，然后得出最后的凸多边形，然后n^2枚举求最远点对即可。这里用到直线切割一个凸多边形的算法。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#define Mod 1000000007
#define pi acos(-1.0)
#define eps 1e-8
using namespace std;

struct Point{
    double x,y;
    Point(double x=, double y=):x(x),y(y) {}
    void input() { scanf("%lf%lf",&x,&y); }
};
typedef Point Vector;
struct Line{
    Point p;
    Vector v;
    double ang;
    Line(){}
    Line(Point p, Vector v):p(p),v(v) { ang = atan2(v.y,v.x); }
    Point point(double t) { return Point(p.x + t*v.x, p.y + t*v.y); }
    bool operator < (const Line &L)const { return ang < L.ang; }
};
int dcmp(double x) {
    if(x < -eps) return -;
    if(x > eps) return ;
    return ;
}
template <class T> T sqr(T x) { return x * x;}
Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }
Vector operator - (Vector A, Vector B) { return Vector(A.x - B.x, A.y - B.y); }
Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); }
Vector operator / (Vector A, double p) { return Vector(A.x/p, A.y/p); }
bool operator < (const Point& a, const Point& b) { return a.x < b.x || (a.x == b.x && a.y < b.y); }
bool operator >= (const Point& a, const Point& b) { return a.x >= b.x && a.y >= b.y; }
bool operator <= (const Point& a, const Point& b) { return a.x <= b.x && a.y <= b.y; }
bool operator == (const Point& a, const Point& b) { return dcmp(a.x-b.x) ==  && dcmp(a.y-b.y) == ; }
double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; }
double Length(Vector A) { return sqrt(Dot(A, A)); }
double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Length(A) / Length(B)); }
double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x; }
Vector VectorUnit(Vector x){ return x / Length(x);}
Vector Normal(Vector x) { return Point(-x.y, x.x) / Length(x);}
double angle(Vector v) { return atan2(v.y, v.x); }

Point GetLineIntersection(Line A, Line B) {
    Vector u = A.p - B.p;
    double t = Cross(B.v, u) / Cross(A.v, B.v);
    return A.p + A.v*t;
}
double DisP(Point A,Point B) {
    return Length(B-A);
}
int LineCrossPolygon(Point& L1,Point& L2,Point* p,int n,Point* poly) {
    int m = ;
    for(int i=,j;i<n;i++) {
        if(dcmp(Cross(L1-p[i],L2-p[i])) >= ) { poly[m++] = p[i]; continue; }
        j = (i-+n)%n;
        if(dcmp(Cross(L1-p[j],L2-p[j])) > ) poly[m++] = GetLineIntersection(Line(L1,L2-L1),Line(p[j],p[i]-p[j]));
        j = (i++n)%n;
        if(dcmp(Cross(L1-p[j],L2-p[j])) > ) poly[m++] = GetLineIntersection(Line(L1,L2-L1),Line(p[j],p[i]-p[j]));
    }
    return m;
}

Line L[];
Point poly[][],p[],q1,q2;
int len[];

int main()
{
    int i,j,pre,now,n;
    double r;
    while(scanf("%d%lf",&n,&r)!=EOF)
    {
        poly[][] = Point(-,-);
        poly[][] = Point(,-);
        poly[][] = Point(,);
        poly[][] = Point(-,);
        len[pre = ] = ;
        for(i=;i<n;i++) p[i].input();
        for(i=;i<n;i++) {
            now = pre^;
            Vector nv = Normal(p[i]-p[(i+)%n]);
            q1 = p[i] + nv*r; q2 = q1+p[(i+)%n]-p[i];
            len[now] = LineCrossPolygon(q2,q1,poly[pre],len[pre],poly[now]);
            pre = now;
        }
        double Maxi = -Mod;
        for(i=;i<len[now];i++)
            for(j=i;j<len[now];j++) {
                if(dcmp(DisP(poly[now][i],poly[now][j])-Maxi) > ) {
                    Maxi = DisP(poly[now][i],poly[now][j]);
                    q1 = poly[now][i], q2 = poly[now][j];
                }
            }
        printf("%.6f %.6f %.6f %.6f\n",q1.x,q1.y,q2.x,q2.y);
    }
    return ;
}