java数据结构之二叉树的定义和递归实现

定义
最多有两棵子树的有序树，称为二叉树。二叉树是一种特殊的树。
递归定义：二叉树是n(n>=0)个有限结点构成的集合。N=0称为空二叉树；n>0的二叉树由一个根结点和两互不相交的，分别称为左子树和右子树的二叉树构成。
二叉树中任何结点的第1个子树称为其左子树，左子树的根称为该结点的左孩子；二叉树中任何结点的第2个子树称为其右子树，左子树的根称为该结点的右孩子。如下图是一个二叉树：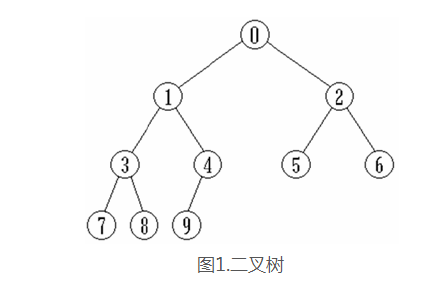

满二叉树和完全二叉树
在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且叶子结点都在同一层上，这样的二叉树称作满二叉树。一棵深度为k且由2k-1个结点的二叉树称为满二叉树。
如果一棵具有n个结点的二叉树的结构与满二叉树的前n个结点的结构相同，这样的二叉树称作完全二叉树。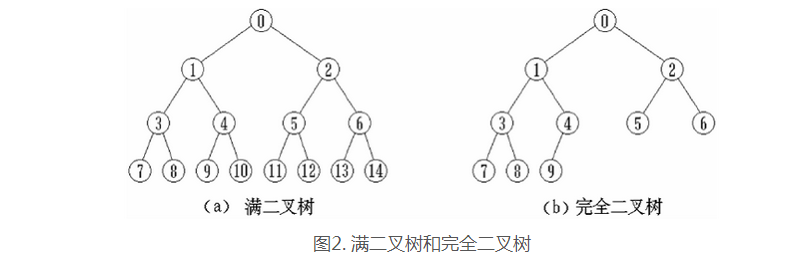

基本性质
这里规定二叉树的根结点的层次为1。
性质1：则二叉树的第i 层最多有2i-1个结点（在此二叉树的层次从1开始，i≥1）
性质2：深度为k的二叉树最多有2k-1个结点。(k≥1)
性质3：对任何一棵二叉树T, 如果其叶结点个数为n0, 度为2的非叶结点个数为n2, 则有
             n0 = n2 + 1

性质4：具有 n(n>0)个结点的完全二叉树的深度为⎣log2n⎦+1；⎦x⎦表示不超过x的最大整数。
性质5：如果对一棵有n个结点的完全二叉树的结点按层序编号（从第1层到第⎣l og2n⎦ +1层，每层从左到右）,则对任一结点i（1≤i≤n),有：
(1)如果i=1，则结点i无双亲，是二叉树的根；如果i>1，则其双亲是结点⎣i/2⎦。
(2) 如果2i<=n, 则结点i的左孩子结点是2i；否则，结点i为叶子结点，无左孩子结点。
(3)如果2i＋1<=n，则结点i的右孩子是结点2i＋1; 否则，结点i为叶子结点，无右孩子结点。

抽象数据类型
数据元素：具有相同特性的数据元素的集合。
结构关系：树中数据元素间的结构关系由二叉树的定义确定。
基本操作：树的主要操作有
（1）创建树IntTree(&T)
（2）销毁树DestroyTree(&T)
（3）构造树CreatTree(&T，deinition)
（4）置空树ClearTree(&T)
（5）判空树TreeEmpty(T)
（6）求树的深度TreeDepth(T)
（7）获得树根Root(T)
（8）获取结点Value(T，cur_e，&e)，将树中结点cur_e存入e单元中。
（9）数据赋值Assign(T，cur_e，value)，将结点value，赋值于树T的结点cur_e中。
（10）获得双亲Parent(T，cur_e)，返回树T中结点cur_e的双亲结点。
（11）获得最左孩子LeftChild(T，cur_e)，返回树T中结点cur_e的最左孩子。
（12）获得右兄弟RightSibling(T，cur_e)，返回树T中结点cur_e的右兄弟。
（13）插入子树InsertChild(&T，&p，i，c)，将树c插入到树T中p指向结点的第i个子树之前。
（14）删除子树DeleteChild(&T，&p，i)，删除树T中p指向结点的第i个子树。
（15）遍历树TraverseTree(T，visit())

二叉树的实现
二叉树接口BTree
    package datastructure.tree.btree;  
      
    public interface BTree {  
        /**
         * 添加左子树
         * @param lChild 左子树
         */  
        public void addLeftTree(BTree lChild);  
        /**
         * 添加右子树
         * @param rchild 右子树
         */  
        public void addRightTree(BTree rchild) ;  
        /**
         * 置空树
         */  
        public void clearTree();  
        /**
         * 求树的深度
         * @return 树的深度
         */  
        public int dept();  
        /**
         * 求左孩子 结点
         * @return
         */  
        public BTree getLeftChild();  
          
        /**
         * 求右孩子结点
         * @return
         */  
        public BTree getRightChild();  
        /**
         * 获得根结点的数据
         * @return
         */  
        public Object getRootData();  
        /**
         * 是否有左子树
         * @return
         */  
        public boolean hasLeftTree();  
        /**
         * 是否有右子树
         * @return
         */  
        public boolean hasRightTree();  
        /**
         * 判断是否为空树
         * @return 如果为空，返回true,否则返回false
         */  
        public boolean isEmpty();  
        /**
         * 判断是否为叶子结点
         * @return
         */  
        public boolean isLeaf();  
        /**
         * 删除左子树
         */  
        public void removeLeftChild();  
        /**
         * 删除右子树
         */  
        public void removeRightChild();  
        /**
         * 获得树根
         * @return 树的根
         */  
        public BTree root();  
        /**
         * 设置根结点的数据
         */  
        public void setRootData(Object data);  
        /**
         * 求结点数
         * @return 结点的个数  
         */  
        public int size();  
    }

二叉链表的实现
    package datastructure.tree.btree;  
      
    public class LinkBTree implements BTree {  
        private Object data;  
        private BTree lChild;  
        private BTree rChild;  
          
        public LinkBTree() {  
            this.clearTree();  
        }  
        public LinkBTree(Object data) {  
            this.data = data;  
            this.lChild = null;  
            this.rChild = null;  
        }  
        @Override  
        public void addLeftTree(BTree lChild) {  
            this.lChild = lChild;  
        }  
      
        @Override  
        public void addRightTree(BTree rChild) {  
            this.rChild = rChild;  
        }  
      
        @Override  
        public void clearTree() {  
            this.data = null;  
            this.lChild = null;  
            this.rChild = null;  
        }  
      
        @Override  
        public int dept() {  
            return dept(this);  
        }  
          
        private int dept(BTree btree) {  
            if(btree.isEmpty()) {  
                return 0;  
            }else if(btree.isLeaf()) {  
                return 1;  
            } else {  
                if(btree.getLeftChild() == null) {  
                    return dept(btree.getRightChild()) + 1;  
                } else if(btree.getRightChild() == null) {  
                    return dept(btree.getLeftChild()) + 1;  
                } else {  
                    return Math.max(dept(btree.getLeftChild()), dept(btree.getRightChild()))+1;  
                }  
            }  
        }  
      
        @Override  
        public BTree getLeftChild() {  
            return lChild;  
        }  
      
      
        @Override  
        public BTree getRightChild() {  
            return rChild;  
        }  
      
        @Override  
        public Object getRootData() {  
            return data;  
        }  
      
        @Override  
        public boolean hasLeftTree() {  
            if(lChild != null)  
                return true;  
            return false;  
        }  
      
        @Override  
        public boolean hasRightTree() {  
            if(rChild != null)  
                return true;  
            return false;  
        }  
      
        @Override  
        public boolean isEmpty() {  
            if((lChild == null && rChild == null && data == null) || this == null) {  
                return true;  
            }  
            return false;  
        }  
          
        @Override  
        public boolean isLeaf() {  
            if(lChild == null && rChild == null) {  
                return true;  
            }  
            return false;  
        }  
      
        @Override  
        public void removeLeftChild() {  
            lChild = null;  
        }  
      
        @Override  
        public void removeRightChild() {  
            rChild = null;  
        }  
        @Override  
        public BTree root() {  
            return this;  
        }  
        @Override  
        public void setRootData(Object data) {  
            this.data = data;  
        }  
        @Override  
        public int size() {  
            return size(this);  
        }  
        private int size(BTree btree) {  
            if(btree == null)   
                return 0;  
            else if(btree.isLeaf())   
                return 1;  
            else {  
                if(btree.getLeftChild() == null) {  
                    return size(btree.getRightChild()) + 1;  
                } else if(btree.getRightChild() == null) {  
                    return size(btree.getLeftChild()) + 1;  
                } else {  
                    return size(btree.getLeftChild()) + size(btree.getRightChild()) + 1;  
                }  
            }   
        }  
          
      
    }

二叉树的遍历
 二叉树的遍历是指按照一定的次序访问树中所有结点，并且每个结点只被访问一次的过程。通常的遍历有三种方式，分别是：前序遍历、中序遍历和后序遍历，假设根结点、左孩子结点和右孩子结点分别用D、R、L表示，则前序遍历、中序遍历和后序遍历的顺序分别为DLR、LDR、LRD。所谓访问某结点，一般指对结点中的数据进行某种操作。所以，我们可以定义一个对结点中的数据进行操作的接口Visit，让所有遍历树的类实现这个接口。
Visit接口：

package datastructure.tree;  
    /**
     * 对结点进行操作的接口
     * @author Administrator
     *
     */  
    public interface Visit {  
        /**
         * 对结点进行某种操作
         * @param btree 树的结点
         */  
        public void visit(BTree btree);  
    }

遍历二叉树

package datastructure.tree;  
    /**
     * 遍历二叉树
     * @author Administrator
     *
     */  
    public class OrderBTree implements Visit{  
        /**
         * 前序遍历
         * @param root 根结点
         */  
        public void preOrder(BTree root) {  
            visit(root);  
            if(root.getLeftChild() != null) {  
                preOrder(root.getLeftChild());  
            }  
            if(root.getRightChild() != null) {  
                preOrder(root.getRightChild());  
            }  
        }  
        /**
         * 中序遍历
         * @param root 根结点
         */  
        public void inOrder(BTree root) {  
            if(root.getLeftChild() != null)  
                inOrder(root.getLeftChild());  
            visit(root);  
            if(root.getRightChild() != null) {  
                //System.out.println("true");  
                inOrder(root.getRightChild());  
            }  
        }  
        /**
         * 后序遍历
         * @param root 根结点
         */  
        public void postOrder(BTree root) {  
            if(root.getLeftChild() != null)  
                postOrder(root.getLeftChild());  
            if(root.getRightChild() != null)  
                postOrder(root.getRightChild());  
            visit(root);  
        }  
      
        @Override  
        public void visit(BTree btree) {  
            System.out.print(btree.getRootData() + "\t");  
        }  
      
    }

二叉树的测试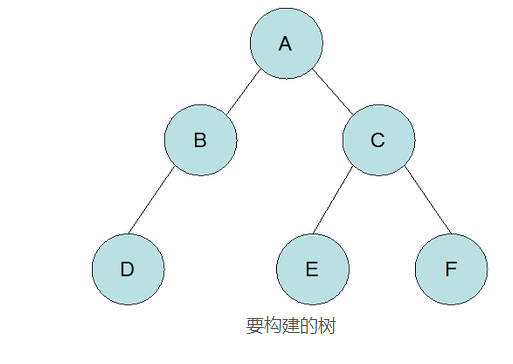

    package datastructure.tree;  
    /**
     * 测试二叉树
     * @author Administrator
     *
     */  
    public class BTreeTest {  
        public static void main(String args[]) {  
            BTree btree = new LinkBTree('A');  
            BTree bt1, bt2, bt3, bt4;  
            bt1 = new LinkBTree('B');  
            btree.addLeftTree(bt1);  
            bt2 = new LinkBTree('D');  
            bt1.addLeftTree(bt2);  
              
            bt3 =  new LinkBTree('C');  
            btree.addRightTree(bt3);  
            bt4 =  new LinkBTree('E');  
            bt3.addLeftTree(bt4);  
            bt4 =  new LinkBTree('F');  
            bt3.addRightTree(bt4);  
              
            System.out.println("树的深度：" + btree.dept());  
            System.out.println("树的结点数：" + btree.size());  
            System.out.println("是否为空树：" + btree.isEmpty());  
            System.out.println("是否为叶子结点：" + btree.isLeaf());  
            System.out.println("最左下边结点是否为叶子结点：" + btree.getRightChild().getRightChild().isLeaf());  
            System.out.println("root结点：" + btree.root());  
              
            OrderBTree order = new OrderBTree();  
            System.out.println("\n前序遍历：");  
            order.preOrder(btree);  
            System.out.println("\n中序遍历：");  
            order.inOrder(btree);  
            System.out.println("\n后序遍历：");  
            order.postOrder(btree);  
              
            btree.removeLeftChild();  
            System.out.println("\n删除左子树后中序遍历为：");  
            order.inOrder(btree);  
        }  
    }

结果如下:
树的深度：3
树的结点数：6
是否为空树：false
是否为叶子结点：false
最左下边结点是否为叶子结点：true
root结点：datastructure.tree.LinkBTree@dc8569

前序遍历：
A B DCEF
中序遍历：
D B AECF
后序遍历：
D B EFCA
删除左子树后中序遍历为：
A E CF

转载至：http://blog.csdn.net/luoweifu/article/details/9077521