Levenshtein Distance莱文斯坦距离算法来计算字符串的相似度

Levenshtein Distance莱文斯坦距离定义：

数学上，两个字符串a、b之间的莱文斯坦距离表示为levab(|a|, |b|）。

levab(i, j) = max(i, j)  如果min(i, j) = 0;

=  min(levab(i - 1, j) + 1, levab(i, j-1) + 1, levab(i - 1, j - 1) + 1)     (ai != bj)

否则其中ai != bj 是指示函数，当ai != bj 时为1， 否则为0。

核心公式就是下面：

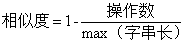            （1）

转

1.百度百科介绍：

Levenshtein 距离，又称编辑距离，指的是两个字符串之间，由一个转换成另一个所需的最少编辑操作次数。

许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

编辑距离的算法是首先由俄国科学家Levenshtein提出的，故又叫Levenshtein Distance。

2.用途

模糊查询

3.实现过程

a.首先是有两个字符串,这里写一个简单的 abc和abe

b.将字符串想象成下面的结构。

A处 是一个标记，为了方便讲解，不是这个表的内容。

	abc	a	b	c
abe	0	1	2	3
a	1	A处
b	2
e	3

c.来计算A处 出得值

它的值取决于：左边的1、上边的1、左上角的0.

按照Levenshtein distance的意思：

上面的值和左面的值都要求加1，这样得到1+1=2。

A处 由于是两个a相同，左上角的值加0.这样得到0+0=0。

这是后有三个值，左边的计算后为2，上边的计算后为2，左上角的计算为0，所以A处 取他们里面最小的0.

d.于是表成为下面的样子

	abc	a	b	c
abe	0	1	2	3
a	1	0
b	2	B处
e	3

在B处 会同样得到三个值，左边计算后为3，上边计算后为1，在B处 由于对应的字符为a、b，不相等，所以左上角应该在当前值的基础上加1，这样得到1+1=2，在（3,1,2）中选出最小的为B处的值。

e.于是表就更新了

	abc	a	b	c
abe	0	1	2	3
a	1	0
b	2	1
e	3	C处

C处 计算后：上面的值为2，左边的值为4，左上角的：a和e不相同，所以加1，即2+1，左上角的为3。

在（2,4,3）中取最小的为C处 的值。

f.于是依次推得到

		a	b	c
	0	1	2	3
a	1	A处 0	D处 1	G处 2
b	2	B处 1	E处 0	H处 1
e	3	C处 2	F处 1	I处 1

I处: 表示abc 和abe 有1个需要编辑的操作。这个是需要计算出来的。

同时，也获得一些额外的信息。

A处: 表示a      和a      需要有0个操作。字符串一样

B处: 表示ab    和a      需要有1个操作。

C处: 表示abe  和a      需要有2个操作。

D处: 表示a      和ab    需要有1个操作。

E处: 表示ab    和ab    需要有0个操作。字符串一样

F处: 表示abe  和ab    需要有1个操作。

G处: 表示a      和abc   需要有2个操作。

H处: 表示ab    和abc    需要有1个操作。

I处: 表示abe   和abc    需要有1个操作。

g.计算相似度

先取两个字符串长度的最大值maxLen，用 1-（需要操作数/maxLen），得到相似度。

例如abc 和abe 一个操作，长度为3，所以相似度为1-1/3=0.666。

4.代码实现

直接能运行， 复制过去就行。

5.猜测原理

为什么这样就能算出相似度了？

首先在连续相等的字符就可以考虑到

红色是取值的顺序。

1.今天周一    天周一

		天	周	一
	0	1	2	3
今	1	1	2	3
天	2	1	2	3
周	3	2	1	3
一	4	3	3	1

实现是去掉“今”，一步完成。

2.听说马上就要放假了 你听说要放假了

		你	听	说	要	放	假	了
	0	1	2	3	4	5	6	7
听	1	1	1	2	3	4	5	6
说	2	2	2	1	2	3	4	5
马	3	3	3	2	2	3	4	5
上	4	4	4	3	3	3	4	5
就	5	5	5	4	4	4	4	5
要	6	6	6	5	4	5	5	5
放	7	7	7	6	5	4	5	6
假	8	8	8	7	6	5	4	6
了	9	9	9	8	7	6	6	4

这两个字符串是：

去掉“你”，加上“马上就”，总共四步操作。