算法设计:UNION-FIND算法实现
在上周的算法设计课程中,我们学习了UNION-FIND算法,该算法用来对不相交集进行查询与合并操作,但任何优秀的算法都必须要用实际的代码来进行实现,接下来我们就来看看具体的代码实现
1. 不相关集数据结构的存储方式
一般来说,对于一个不相关集A = {1, 2, ..., n} 来说,我们使用两个长度为n的数组p[] 和 rank[] 来表示。
p[] 中,数组下标表示所对应的元素,数组值表示该元素对应的父节点,没有父节点时值为0,如a[1] = 2 便表示元素1的父节点为2
rank[] 表示数组元素的秩,一般用来表示该节点的高度,初始值全为零。
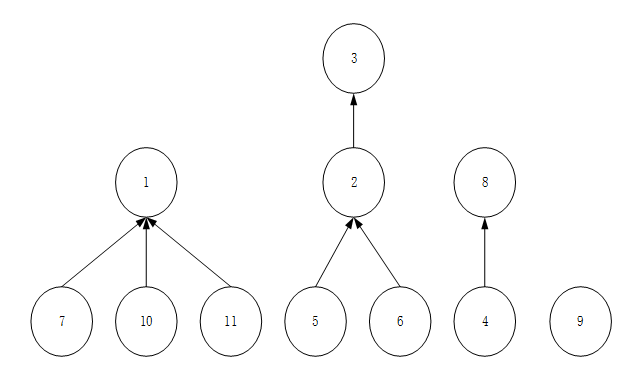
上图的不相交集结构用数组表示为下图:
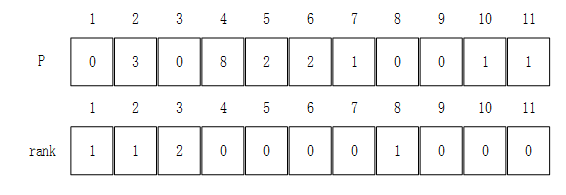
2. UNION-FIND算法及其代码实现
UNION-FIND算法包含两个方法FIND(x) 与 UNION(x, y)
FIND(x):用来寻找包含x的根,算法如下(书P83)
- y←x
- while p(y)≠null{寻找包含x的树的根}
- y←p(y)
- end while
- root←y;y←x
- while p(y)≠null {执行路径压缩}
- w←p(y)
- p(y)←root
- y←w
- end while
- return root
UNION(x, y):用来合并两个树,算法如下(书P83)
- u←FIND(x);v←FIND(y)
- if rank(u) ≦ rank(v) then
- p(u)←v
- if rank(u) = rank(v) then rank(v)←rank(v)+1
- else p(v)←u
- end if
具体代码实现如下:
//不相交集及union-find算法的练习
public class Gather { //声明不相交集类
private int p[] = new int[50]; //存放元素父节点
private int rank[] = new int[50]; //存放元素的秩
public int length; //不相交集的长度
public Gather(int length)
{
this.length = length;
}
//寻找指定结点
public int find(int n)
{
int i = n;
/*这里的i,n 分别对应书上算法中的y,x
* 同理union中的a,b对应书上算法的u,v*/
int root, t;
while(p[i]!=0)
//向上寻找根结点
i = p[i];
root = i;
i = n; //两个指针分别指向根结点与初始结点
while(p[i]!=0)
{
//执行路径压缩
t = p[i]; //t指向i的父节点
p[i] = root; //将i的父节点设为根结点
i = t; //指针上移
}
return root;
}
//将两个树合并
public void union(int x,int y)
{
int a = find(x);
int b = find(y);
//当a的秩小于等于b的秩时,以b作为父结点
if(rank[a] <= rank[b])
{
p[a] = b;
//当a的秩等于b的秩时,b的秩+1
if(rank[a] == rank[b])
rank[b]++;
}
else p[b] = a; //当a的秩大于b的秩时,a作为父节点
}
//输出不相交集
public void dispGather()
{
System.out.print("元素值:");
for(int i=1;i<length;i++)
System.out.print(i + " "); //输出所有元素
System.out.println();
System.out.print("父节点:");
for(int i=1;i<length;i++)
System.out.print(p[i] + " "); //输出所有元素对应的父节点值
System.out.println("\n");
}
}
1. 数据测试
写好了代码,我们需要用一些数据来测试一下我们的代码,我们采用书上P83的例4.4作为实例。
例4.4 设S = {1, 2, ..., 9},考虑用下面的合并和寻找序列:UNION(1, 2), UNION(3,4), UNION(5,6), UNION(7,8), UNION(2,4), UNION(8,9), UNION(6,8), FIND(5), UNION(4,8), FIND(1)

创建一个Gather对象并输出其初始状态(需要注意的是,我们的算法是下标从1开始的,而java中数组是从下标0开始的,所以我们定义长度为n的不相交集时,输入数字必须为n+1)

结果图表示如下:
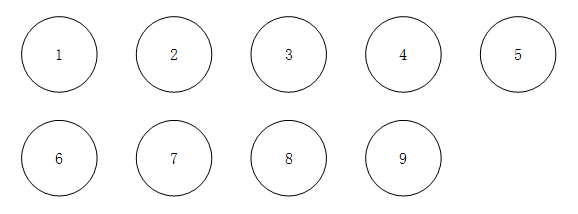

由于篇幅关系,我们就不像书上和代码上那样分步看结果了,直接跳到最后的输出:

用图表示如下:
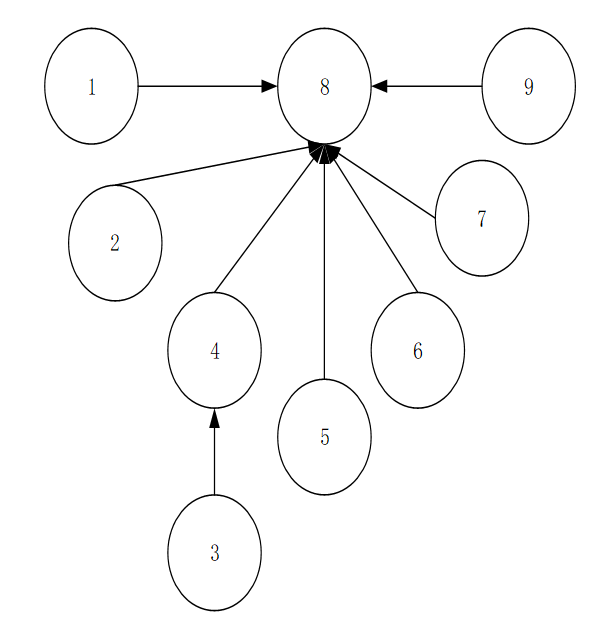
算法设计:UNION-FIND算法实现的更多相关文章
- 南大算法设计与分析课程复习笔记(1) L1 - Model of computation
一.计算模型 1.1 定义: 我们在思考和处理算法的时候是机器无关.实现语言无关的.所有的算法运行在一种“抽象的机器”之上,这就是计算模型. 1.2 种类 图灵机是最有名的计算模型,本课使用更简单更合 ...
- OOP: One pont of view of OOP与基于算法设计的区别
..摘自<C++网络编程 卷1:运用ACE和模式消除复杂性> <C++ Network Programming Volume 1 Mastering Complexity with ...
- Python数据结构与算法设计总结篇
1.Python数据结构篇 数据结构篇主要是阅读[Problem Solving with Python]( http://interactivepython.org/courselib/static ...
- 算法设计和数据结构学习_5(BST&AVL&红黑树简单介绍)
前言: 节主要是给出BST,AVL和红黑树的C++代码,方便自己以后的查阅,其代码依旧是data structures and algorithm analysis in c++ (second ed ...
- Data Structure 之 算法设计策略
1. 穷举法 基本思想:列举问题的所有可能解,并用约束条件逐一进行判定,找出符合约束条件的解. 穷举法的关键在于问题的可能解的列举和可能解的判别. 例如:凑数问题 2. 递归技术 定义:直接或间接调用 ...
- IK分词算法设计总结
IK分词算法设计思考 加载词典 IK分词算法初始化时加载了“敏感词”.“主词典”.“停词”.“量词”,如果这些词语的数量很多,怎么保证加载的时候内存不溢出 分词缓冲区 在分词缓冲区中进行分词操作,怎么 ...
- 【技术文档】《算法设计与分析导论》R.C.T.Lee等·第7章 动态规划
由于种种原因(看这一章间隔的时间太长,弄不清动态规划.分治.递归是什么关系),导致这章内容看了三遍才基本看懂动态规划是什么.动态规划适合解决可分阶段的组合优化问题,但它又不同于贪心算法,动态规划所解决 ...
- 算法设计手冊(第2版)读书笔记, Springer - The Algorithm Design Manual, 2ed Steven S.Skiena 2008
The Algorithm Design Manual, 2ed 跳转至: 导航. 搜索 Springer - The Algorithm Design Manual, 2ed Steven S.Sk ...
- 【算法设计与分析基础】24、kruskal算法详解
首先我们获取这个图 根据这个图我们可以得到对应的二维矩阵图数据 根据kruskal算法的思想,首先提取所有的边,然后把所有的边进行排序 思路就是把这些边按照从小到大的顺序组装,至于如何组装 这里用到并 ...
随机推荐
- python_微信 跳一跳
今天用python刷了一下微信跳一跳游戏得分数. 不是仅仅是玩一玩,而是为了把开发环境搭建好.(这个借口好) 参考: http://blog.csdn.net/LittleBeautiful/arti ...
- 移动端上下滑动事件之--坑爹的touch.js
下面的方法,不知道是操作方法不对还是啥. 在 zepto.js 里面加那一段代码不起作用 百度的 touch.js 是可以用的,但是使用方式 和 zepto有点不一样. 解决方案:参照这个链接地址 ...
- 用Python爬虫爬取炉石原画卡牌图片
前段时间看了点Python的语法以及制作爬虫常用的类库,于是动手制作了一个爬虫尝试爬取一些炉石原画图片.本文仅记录对特定目标网站的分析过程和爬虫代码的编写过程.代码功能很局限,无通用性,仅作为一个一般 ...
- python第八课——random模块的使用
2.2.如何获取随机整数值? 引入random模块的使用 randint(a,b)函数:作用:返回给程序一个[a,b]范围内的随机整数注意:含头含尾闭区间 思路步骤: 第一步:导入random模块到相 ...
- P2110 欢总喊楼记
题目描述 诗经有云: 关关雎鸠,在河之洲.窈窕淑女,君子好逑. 又是一个被风吹过的夏天--一日欢总在图书馆中自习,抬起头来,只见一翩跹女子从面前飘过,真是回眸一笑百媚生,六宫粉黛无颜色!一阵诗情涌上欢 ...
- Windows启动控制台登录模式
效果如下: 实现代码: Set-ItemProperty -Path HKLM:\SOFTWARE\Microsoft\Windows\CurrentVersion\Authentication\Lo ...
- js检测是够断网
方法 一 navigator.onLine 这个html5的 navigator的新特性可以很简单帮我们搞定 HTML5为此定义了一个navigator.onLine属性,这个属性值为true表示 ...
- [转]SVN服务器搭建和使用(一)
Location是指VisualSVN Server的安装目录,Repositorys是指定你的版本库目录.Server Port指定一个端口,Use secure connection勾山表示使用安 ...
- java 输出流 outputstream
一:输入和输出概念 输入流(inputstream):对于java程序来说,从程序写入文件叫做输出. 输出流(outputstream):对于java程序来说,从文件读取数据,到java程序叫做输入. ...
- 使用.Net Core MVC创建Web API
创建.Net Core MVC 打开appsettings.json文件,添加数据库连接 { "Logging": { "LogLevel": { " ...
