codeforces 1140E Palindrome-less Arrays

题目链接：http://codeforces.com/contest/1140/problem/E

题目大意：

如果一个数组的存在一个奇数长的回文就不好。

不是不好的数组是好的。

你可以把-1用1到k中一个数替换。问可以有多少种不同的好数组。

开虚拟赛最后一分钟把它A了，很开心，很开心。

思路：

我们翻译一下，如果存在长度为5的回文就必须会出现长度为3的回文。

也就是说不能出现长度为3回文。

也就是说x[i]!=x[i+2],x[i]!=x[i-2];（x[i]为输入数组）

那我们把数组分为两个数组，按奇偶分。（1，3，5，，，）（2，4，6，，，）

这两个数组就都要满足一个条件x[i]!=x[1+i]&&x[i]!=x[i-1];（相邻两个数不能相等）

然后我们就开始DP啦。

对于奇偶两个数组我就分析一个啦，因为都差不多。（相邻两个数不能相等）

首先，当然是n*k的DP。

DP[a][b]表示到a下为b的方案数。

所以DP[a][b]等于所有DP[a-1][i](1<=i<=k,i!=b)的和。

如果x[a]为-1，就算所有的1到k。

如果x[a]>0,就只算DP[a][x[a]]；

这个可以理解吗？

可以理解就太好了！！！

然而，你在DP的过程中，发现DP[a][i](1<=i<=k)中只可能有两个不同的值（不会超过3个），而且产生不同的值是一个特殊的位置。

你可以先拿小一点的数据打表看看。

也就是说，对于每一个状态。只有两种可能，而不是k种可能。

所以，我们就可以写O（n）的DP了。

我画了两张图给你们看看。

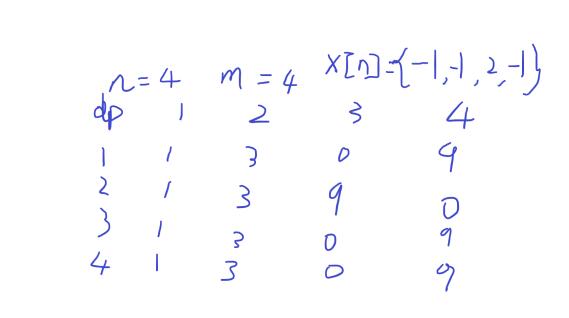
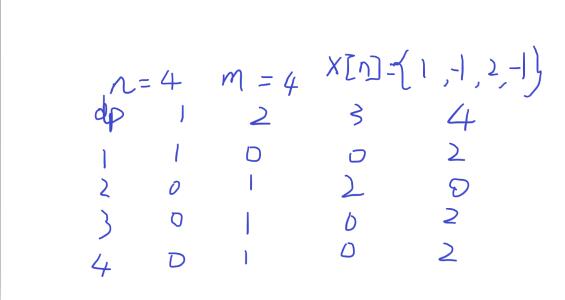
然后到了愉快的贴代码时间了。不是很懂可以私聊QQ：1328247116，也可以下面留言。~~

#include <bits/stdc++.h>
using namespace std;

#define int long long
#define IOS ios::sync_with_stdio(false);
#define endl "\n"
#define MAX 200050
#define mod 998244353

///
int x[MAX];
int dp[MAX];
int dp_1=,dp_1_sum=;
int dp_2=,dp_2_sum=;
int ans[MAX];
///
signed main()
{
    IOS;

    int n,m;
    cin>>n>>m;
    for(int i=;i<=n;i++){
        cin>>x[i];
    }

    if(x[]>){
        dp[]=;
        dp_1=x[],dp_1_sum=;
    }
    else{
        dp[]=;
        dp_1=,dp_1_sum=;
    }

    for(int i=;i<=n;i+=){
        if(x[i]>){
            if(x[i]==dp_1){
                dp_1_sum=(m-)*dp[i-]%mod;
            }
            else{
                dp_1_sum=((m-)*dp[i-]%mod+dp_1_sum)%mod;
            }
            dp_1=x[i];
        }
        else{
            dp[i]=((m-)*dp[i-]%mod+dp_1_sum)%mod;
            dp_1_sum=(m-)*dp[i-]%mod;
        }
    }

    ///
    if(x[]>){
        dp[]=;
        dp_2=x[],dp_2_sum=;
    }
    else{
        dp[]=;
        dp_2=,dp_2_sum=;
    }

    for(int i=;i<=n;i+=){
        if(x[i]>){
            if(x[i]==dp_2){
                dp_2_sum=(m-)*dp[i-]%mod;
            }
            else{
                dp_2_sum=((m-)*dp[i-]%mod+dp_2_sum)%mod;
            }
            dp_2=x[i];
        }
        else{
            dp[i]=((m-)*dp[i-]%mod+dp_2_sum)%mod;
            dp_2_sum=(m-)*dp[i-]%mod;
        }
    }
    int ans;
    if(n%==){
        ans=(dp_1_sum+(m-)*dp[n-]%mod)*(dp_2_sum+(m-)*dp[n]%mod)%mod;
    }
    else{
        ans=(dp_1_sum+(m-)*dp[n]%mod)*(dp_2_sum+(m-)*dp[n-]%mod)%mod;
    }
    cout<<ans;
    return ;
}

/*

*/