The Balance(poj2142)

The Balance

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 5452		Accepted: 2380

Description

Ms. Iyo Kiffa-Australis has a balance and only two kinds of weights to measure a dose of medicine. For example, to measure 200mg of aspirin using 300mg weights and 700mg weights, she can put one 700mg weight on the side of the medicine and three 300mg weights on the opposite side (Figure 1). Although she could put four 300mg weights on the medicine side and two 700mg weights on the other (Figure 2), she would not choose this solution because it is less convenient to use more weights.
You are asked to help her by calculating how many weights are required.

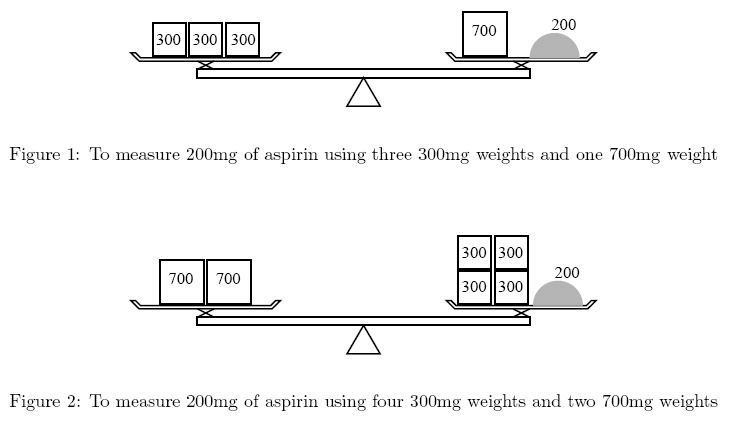
Input

The
input is a sequence of datasets. A dataset is a line containing three
positive integers a, b, and d separated by a space. The following
relations hold: a != b, a <= 10000, b <= 10000, and d <= 50000.
You may assume that it is possible to measure d mg using a combination
of a mg and b mg weights. In other words, you need not consider "no
solution" cases.

The end of the input is indicated by a line containing three zeros separated by a space. It is not a dataset.

Output

The
output should be composed of lines, each corresponding to an input
dataset (a, b, d). An output line should contain two nonnegative
integers x and y separated by a space. They should satisfy the following
three conditions.

• You can measure dmg using x many amg weights and y many bmg weights.
• The total number of weights (x + y) is the smallest among those pairs of nonnegative integers satisfying the previous condition.
• The total mass of weights (ax + by) is the smallest among
  those pairs of nonnegative integers satisfying the previous two
  conditions.

No extra characters (e.g. extra spaces) should appear in the output.

Sample Input

700 300 200
500 200 300
500 200 500
275 110 330
275 110 385
648 375 4002
3 1 10000
0 0 0

Sample Output

1 3
1 1
1 0
0 3
1 1
49 74
3333 1
思路：扩展欧几里德。
首先，如果没有取最小那个条件限制，这就是一道裸的扩展欧几里德。那么考虑那个限制条件。我们用欧几里德求出x，y后，我们先求
x的最小正解，然后代入方程求的y,如果y是正的，假设x要增大，那么y就要减小，当y还是>0由于这时两种砝码在同侧，所以我们可以
考虑下贪心，也就是优先取质量重的取，那么要么就是x取最小正解时要么取y是最小正解时（在x，y都为正的前提下）。那么如果当y<0
原来两个取正肯定要比一个取正一个取负的总和小。同理先取y为最小正，根据（ax+by=c）中x,y的等价性我们可以同样分析y。
那么综合这两种情况我们可以得出这样的结论（x+y）最小要么在x在最下正时取要么在y为最小正时取。

 1 #include<stdio.h>
 2 #include<algorithm>
 3 #include<iostream>
 4 #include<math.h>
 5 #include<stdlib.h>
 6 #include<string.h>
 7 using namespace std;
 8 typedef long long LL;
 9 const long long N=1e6+3;
10 long long MM[1000005];
11 long long quick(long long n,long m);
12 pair<LL,LL>P(long long n,long long m);
13 long long gcd(long long n,long long m);
14 int main(void)
15 {
16         long long i,j,k,p,q;
17         while(scanf("%lld %lld %lld",&k,&p,&q),p!=0&k!=0&q!=0)
18         {
19                 long long zz=gcd(k,p);
20                 k/=zz;
21                 p/=zz;
22                 q/=zz;
23                 pair<LL,LL>SS=P(k,p);
24                 long long x=SS.first;
25                 x*=q;
26                 x=(x%p+p)%p;
27                 long long y=fabs(1.0*(q-x*k)/p);
28                 long long z=SS.second;
29                 z*=q;
30                 z=(z%k+k)%k;
31                 long long xx=fabs(1.0*(q-z*p)/k);
32                 if(xx+z<y+x)
33                         printf("%lld %lld\n",xx,z);
34                 else if(xx+z==y+x)
35                 {
36                         long long cc=x*k+y*p;
37                         long long zz=z*p+xx*k;
38                         if(xx<zz)
39                                 printf("%lld %lld\n",xx,z);
40                         else printf("%lld %lld\n",x,y);
41                 }
42                 else printf("%lld %lld\n",x,y);
43         }
44         return 0;
45 }
46
47 long long quick(long long n,long m)
48 {
49         long long k=1;
50         while(m)
51         {
52                 if(m&1)
53                 {
54                         k=(k%N*n%N)%N;
55                 }
56                 n=n*n%N;
57                 m/=2;
58         }
59         return k;
60 }
61 long long gcd(long long n,long long m)
62 {
63         if(m==0)
64                 return n;
65         if(n%m==0)
66         {
67                 return m;
68         }
69         else return gcd(m,n%m);
70 }
71 pair<LL,LL>P(long long n,long long m)
72 {
73         if(m==0)
74         {
75                 pair<LL,LL>K=make_pair(1,0);
76                 return K;
77         }
78         else
79         {
80                 pair<LL,LL>L=P(m,n%m);
81                 pair<LL,LL>S;
82                 S.first=L.second;
83                 S.second=L.first-(n/m)*L.second;
84                 return S;
85         }
86 }