最小生成树,Prim算法与Kruskal算法,408方向,思路与实现分析

最小生成树,Prim算法与Kruskal算法,408方向,思路与实现分析

最小生成树,老生常谈了,生活中也总会有各种各样的问题,在这里,我来带你一起分析一下这个算法的思路与实现的方式吧~~

在考研中呢,最小生成树虽然是只考我们分析,理解就行,但我们还是要知道底层是怎么实现的,话不多说,进入正题~~

什么是生成树?什么是最小生成树

总所周知,对于一个无向连通图,我们想把他看成一个树的话,那么就不能太乱,也就引出了,如果对于一个生成树(不唯一,满足条件即可),如果砍去它的一条边,则会变成非连通图,如果加上一条边则会形成一个回路,也就是包含图的全部顶点的一个极小连通子图,如下所示~~

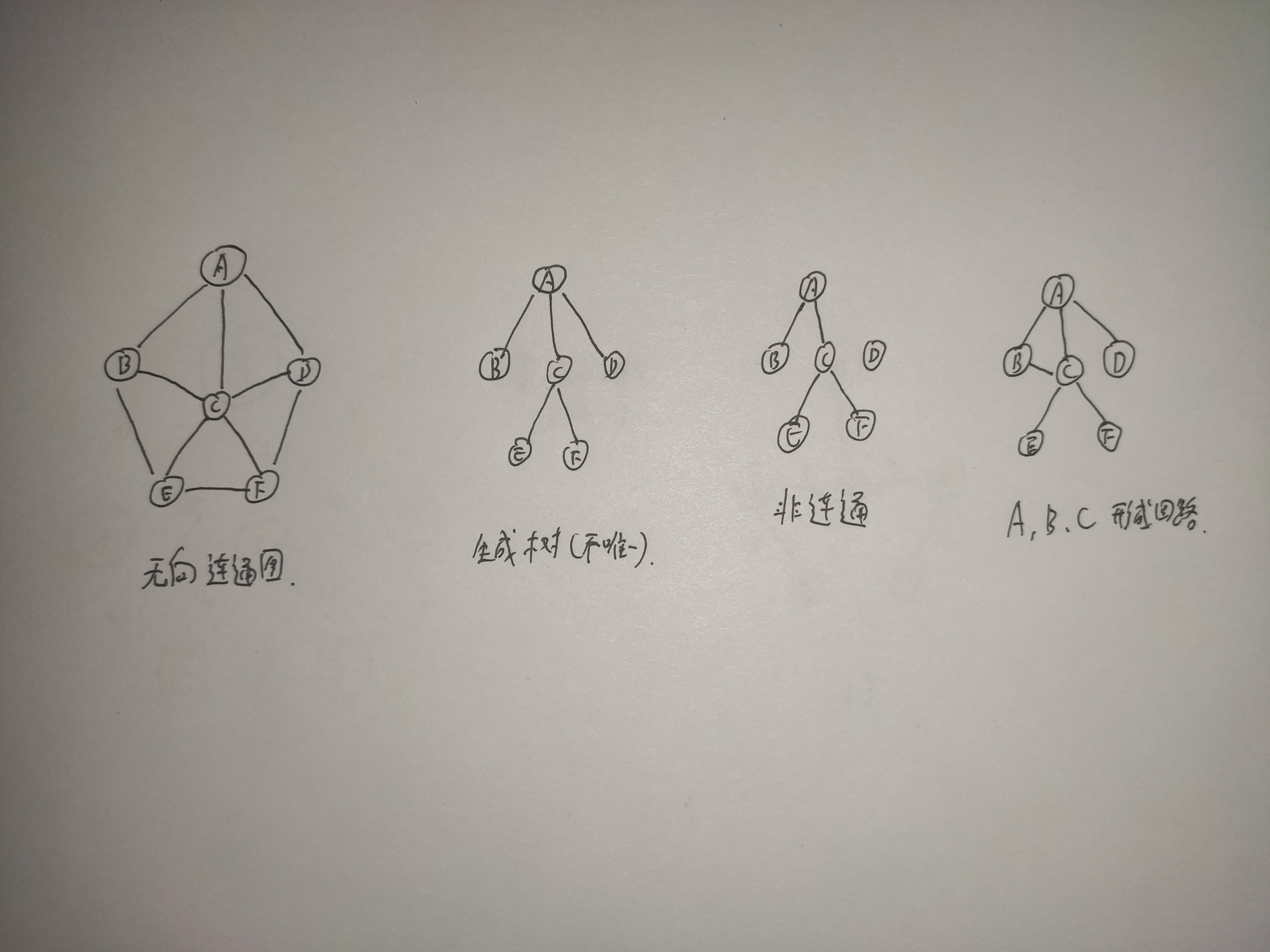
因此,对于顶点数为n的图,生成树应含有n-1条边~~

那么,最小生成树又是什么呢?

当边带权时,我们想要一个生成树,使得带权路径和最小,那么这样的生成树就被我们称作最小生成树(不唯一),也就是边的权值之和最小的生成树(MST,Minimum-Spanning-Tree)~~

那么怎么求一个最小生成树呢?

没错,我们相求一个最小生成树,我们的前辈大牛也想过这个问题,也就引出了两个算法,一个是Prim算法(普里姆),和Kruskal算法(克鲁斯卡尔)~~

先给一个案例我们来分析一下,经典的修路~~

我们想要使得我们这个小镇全都连通,但又花费经济最少(虚线边数值代表所需金钱,也就是权值),该怎么修呢?先给出答案,接下来我们用两个算法分别分析一下思路以及底层实现~~

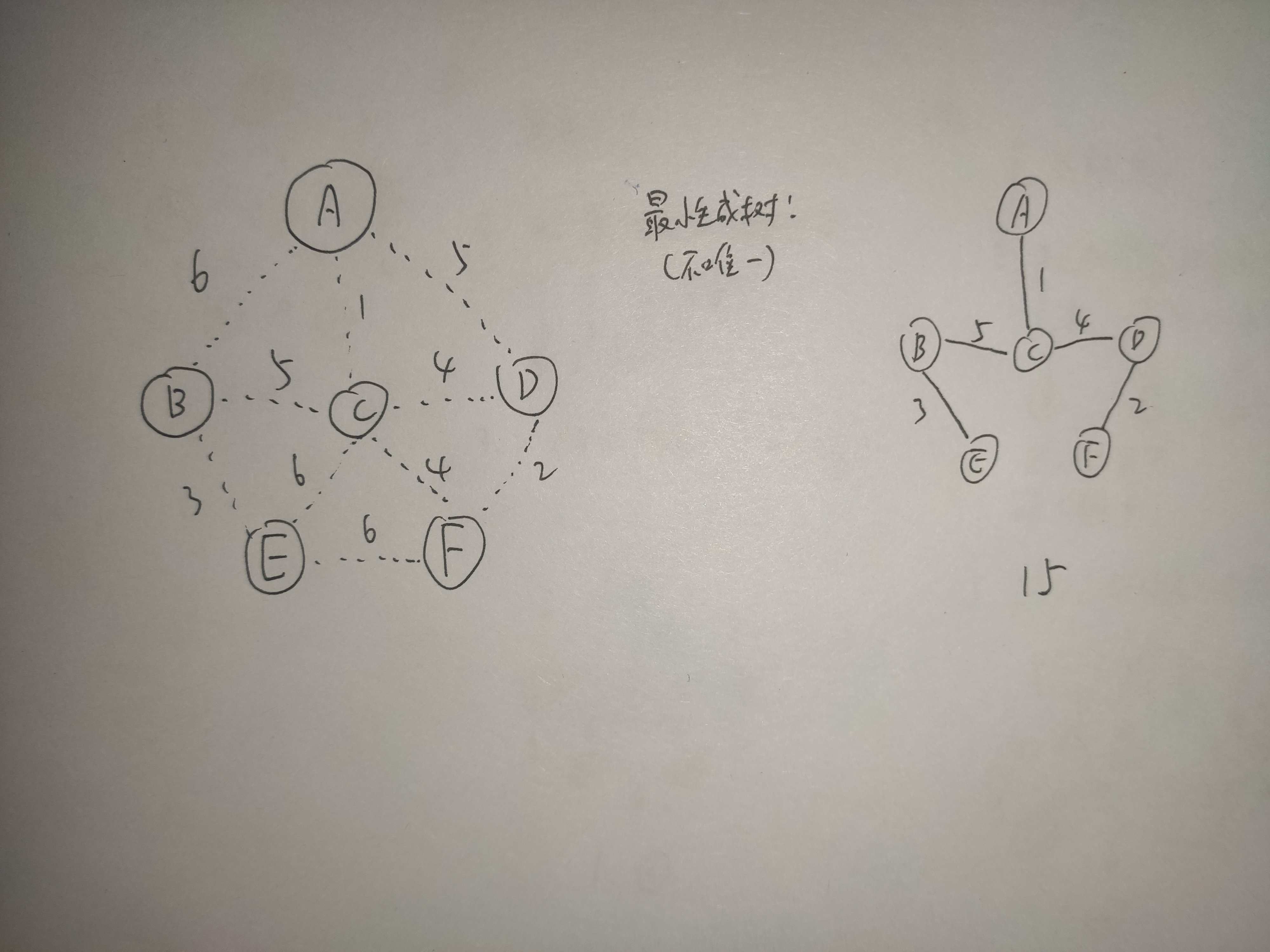
Prim算法(普里姆)思路分析与底层实现

Prim算法:从选取的某一个顶点开始,每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止~~

思路分析:也就是并查集内加新顶点,为了方便理解,我们把并查集每次都纳入的顶点看成一个在一个圈里加入新顶点,不属于圈里的即为连通的顶点,如图所示算法思路~~

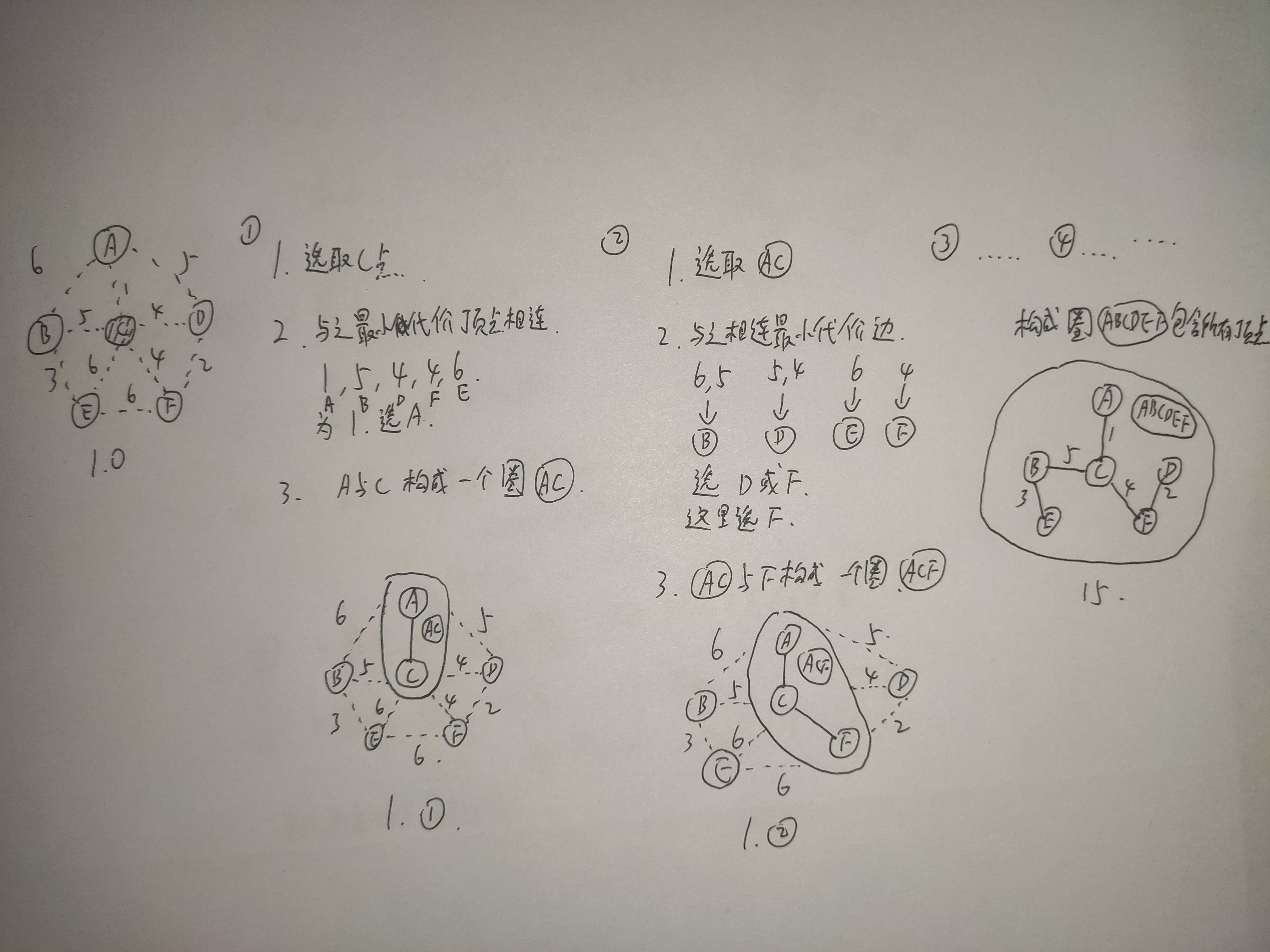
底层实现:我们这里定义两个数组一个为isJoin[]和lowCost[]数组,isJoin[]用来标记是否已加入树,lowCost[]用来表示各节点加入当前树时的最低代价~~

如第一个步骤的时候,只有c点加入了树,那么我们就当c点已经加入了树,也就是说isJoin[6]变为了如表所示(为了方便我们把数组下标换成我们的字母abcdef)~~

	C	A	B	D	E	F
isJoin[6]	1	0	0	0	0	0

此时我们的lowCost[6]对应就应为(没有边直接连通则为无穷):

	C	A	B	D	E	F
lowCost[6]	0	1	5	4	6	4

lowCost最小为1,也就是C与A连接所需代价最小,所以当第1步结束时,我们将A连入树中,修改对应isJoin[6]和lowCost[6]~~

	C	A	B	D	E	F
isJoin[6]	1	1	0	0	0	0

	C	A	B	D	E	F
lowCost[6]	0	0	5	4	6	4

权:1~~

lowCost最小为4,也就是(D或者F)与圈AC连接所需代价最小,所以当第2步结束时,我们将F连入树中,修改对应isJoin[6]和lowCost[6]~~

	C	A	B	D	E	F
isJoin[6]	1	1	0	0	0	1

	C	A	B	D	E	F
lowCost[6]	0	0	5	2	6	0

权:1+4~~

因为现在要和圈ACF连接,D如果想代价最小就可以选择DF连接(2),而不是以前的DC连接(4),2代价更小,这就是lowCost[]用来表示各节点加入当前树时的最低代价的意思~~

重复此过程~~

	C	A	B	D	E	F
isJoin[6]	1	1	0	1	0	1

	C	A	B	D	E	F
lowCost[6]	0	0	5	0	6	0

权:1+4+2~~

接下来

	C	A	B	D	E	F
isJoin[6]	1	1	1	1	0	1

	C	A	B	D	E	F
lowCost[6]	0	0	0	0	3	0

权:1+4+2+5~~

最后

	C	A	B	D	E	F
isJoin[6]	1	1	1	1	1	1

	C	A	B	D	E	F
lowCost[6]	0	0	0	0	0	0

权:1+4+2+5+3=15~~

Kruskal算法(克鲁斯卡尔)思路分析与底层实现

双生关系,Prim是每次选一个连到树里代价最小的顶点构成一个树,Kruskal是每次选一条权值最小的边,使这条边两端连通(如果原本就已经连通就不选),直到所有结点都连通~~

思路分析:上图~~

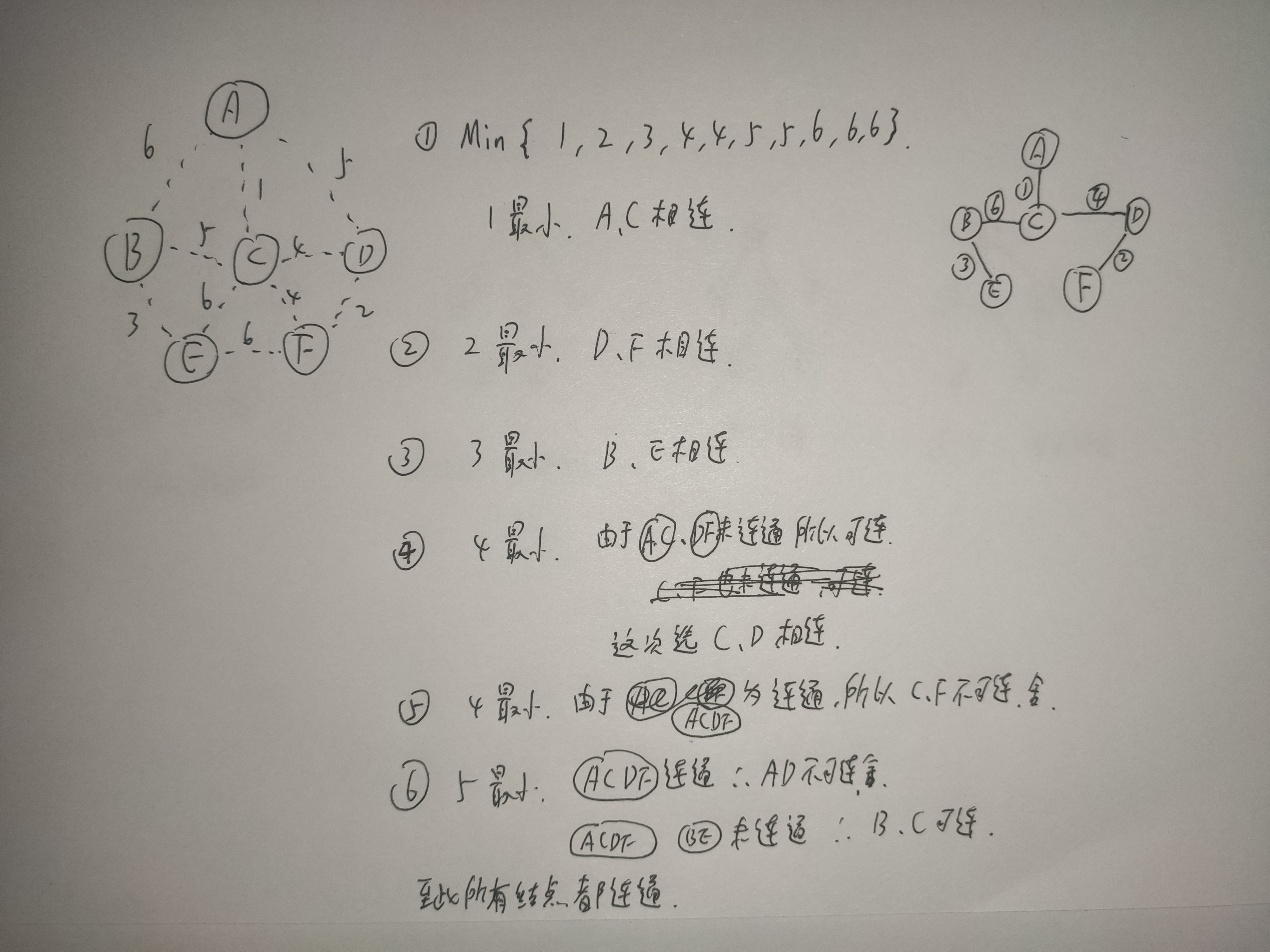
底层实现:并查集~~

按权值排序~~

weight	1	2
1	A	C
2	D	F
3	B	E
4	D	C
4	C	F
5	A	D
5	B	C
6	A	B
6	C	E
6	E	F

依次往下看,1和2两个点是否属于同一集合(先规定所有顶点都属于不同的集合,如果两个顶点相连,则这两个顶点构成了一个集合)~~

如第一次,weight为1,A和C为不同集合,相连,通过~~(集合AC,B,D,E,F)

第二次,weight为2,D和F为不同集合,相连,通过~~(集合AC,DF,B,E)

第三次,weight为3,B和E为不同集合,相连,通过~~(集合AC,DF,BE)

第四次,weight为4,D和C虽然DF是一个集合,AC是一个集合,但DF和AC不是一个集合里的不连通,所以相连,通过~~(集合ACDF,BE)

第五次,weight为4,C和F同属于ACDF集合里,所以不相连,不通过~~(集合ACDF,BE)

第六次,weight为5,A和D同属于ACDF集合里,所以不相连,不通过~~(集合ACDF,BE)

第七次,weight为5,B和C不属于同一个集合里,所以相连,通过~~(集合ABCDEF)

至此成功~~

最小生成树还是简单的,为我们后面学习最短路径做基础,这里大家好好看看,下周我就来谈一谈最短路径的几个算法,这两者很像,但要区分开来~~