STM32CbueIDE 与 J-Link

无论是 STM32CbueIDE 还是 Keil, 在使用 JLink 的时候都不过是先启 JLink 的 GDB 服务，然后再“远程”连接到 GDB 透过 J-Link 支持的命令操作 MCU 的。（在软件的安装目录中一定能找到 "JLinkGDBServer.exe".） 相比于 Keil 的封闭来说 STM32CbueIDE 要好一些，在调试和运行时可以通过控制台输出找到其在启动 JLinkGDBServer 时的参数。

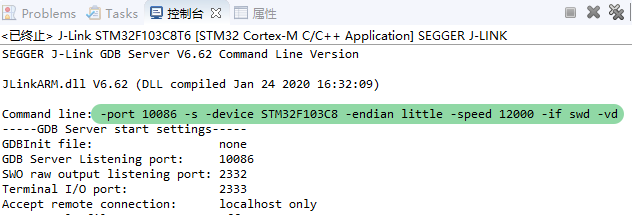
关于在 STM32CbueIDE 中 J-Link 的配置

具体配置项跟 Keil 差不多，实际可参照下图。

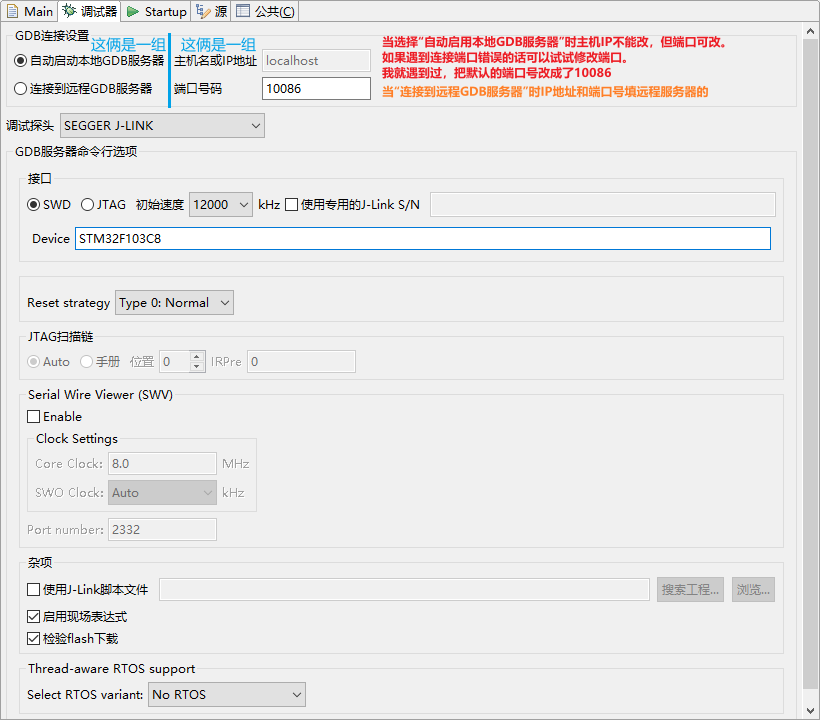
存在的问题（在Windows中）

问题描述

在 Windows 中使用 STM32CbueIDE 与 JLink 的组合存在一个无伤大雅但是却令人十分难受的问题，那就是每次执行 "运行" 后都会在任务栏托盘区域创建一个JLink图标（因为启动了JLinkGDBServer.exe），但是运行成功后这个图标并不会自己消失（进程已经结束了，但是图标不消失），久而久之调程序的次数多了就会在任务栏形成一大堆僵尸图标。

网上说这种情况是进程异常结束造成的，也就是说进程虽然结束了，但是在结束之前没来得及注销任务栏托盘的图标，CbueIDE 果然还是问题多多啊。这种情况只要把鼠标挪到相应的图标上图标就会消失了，但是每次下完程序都特意把鼠标往任务栏上扫一遍的行为也太傻了吧。

System Tray Refresh

System Tray Refresh 是我费劲千辛万苦找到的一个小工具，仅有18.5k. 它的作用就是刷新系统托盘图标，可以令死图标消失。

官网地址：http://visualfantasy.tk/

52破解论坛介绍：https://www.52pojie.cn/thread-659012-1-1.html

Windows 计划任务

原因了解，工具也有了，接下来只需发挥一下聪明才智，交给电脑自己该怎么做就行了——当使用 STM32CbueIDE 给单片机下载完程序后自动清理托盘残留的图标。

任务：运行 SystemTrayRefresh.exe ;

触发条件：检测到启动了 JLinkGDBServer.exe .

关于这种类型计划任务的配置，摘抄了网上的一段内容：请问如何使用任务计划程序中的触发器——“发生事件时”？

实现启动程序A的时候执行相应的计划任务这样的效果,您首先需要开启相关的日志记录:

右键点击开始按钮>运行>secpol.msc

在打开的本地安全策略中依次展开本地策略>审核策略>双击打开右侧的"审核进程跟踪",勾选"审核这些操作"下方的"成功">确定

设置完成后可以随便打开一个应用程序再关闭,然后右键点击开始按钮>事件查看器>Windows日志>安全>可以看到最新一条的事件记录(4688)可以成功记录到刚才启动的程序的事件.

接下来回到任务计划程序中,修改计划任务的触发器,使用"发生事件时"触发>自定义>新建事件筛选器,切换至"XML"标签页,勾选"手动编辑查询",粘贴下面内容:

<QueryList>

  <Query Id="0" Path="Security">

    <Select Path="Security">

    *[System[band(Keywords,9007199254740992) and

    (EventID=4688)]] and

    *[EventData[Data[@Name='NewProcessName'] and

    (Data='C:\Windows\System32\notepad.exe')]]

    </Select>

  </Query>

</QueryList>

注:请将上面代码中倒数第四行Data=''中的内容替换为程序A的完整路径.

然后再继续配置"创建任务"窗口中的"操作"内容.

首先按照教程开启“审核进程跟踪”；然后打开"事件查看器>Windows日志>安全",按日期和时间排序、在筛选器中筛选"4688".
点击一次 STM32CbueIDE 中的 "运行" 按钮，等程序下载完成后返回并刷新一次事件查看器窗口，找到最新的事件查看详情，发现果然是运行 JLink 相关的进程，进程名是 "JLinkGUIServer.exe".
创建计划任务。
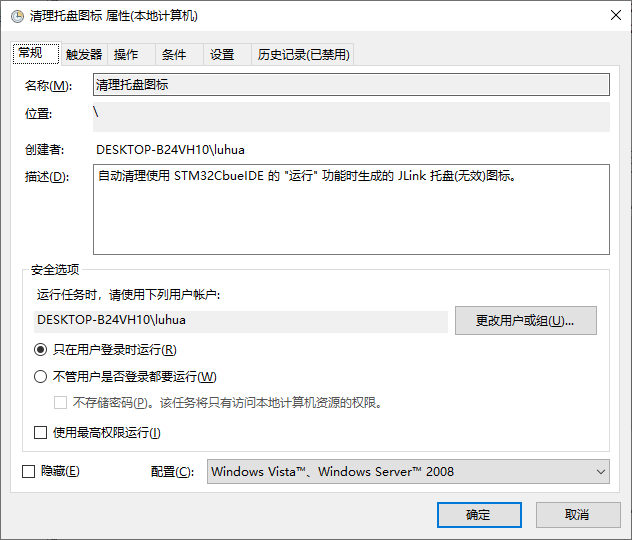
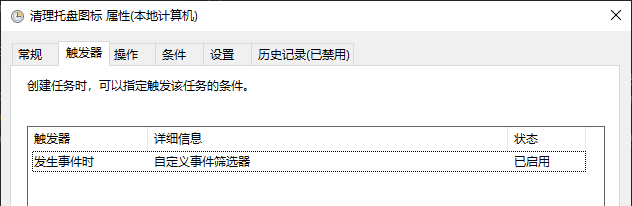
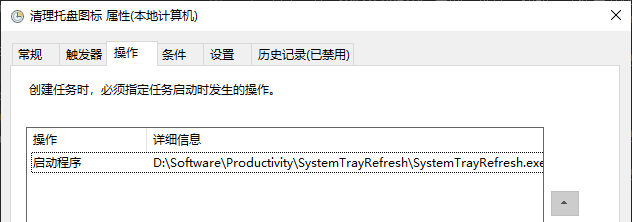
运行再打开 STM32CbueIDE 点击 "运行" 下载一次程序，JLink图标终于干净了，完美！