20210715 noip16

考场

乍一看 T1 像是二分答案，手玩样例发现可以 \(O(k^2)\) 枚举点对，贪心地更新答案，完了？有点不信，先跳了

T2 的形式有点像逆序对，但没啥想法

T3 的式子完全不知道如何处理，一看就是乱搞的题

回来看 T1，原来的想法果然是假的

悲伤的是思考用了 1h10min，导致开始写代码是有点紧张，怕写不完

T2 先尝试了一个假的贪心，过了样例但小数据都过不了拍，又尝试用贪心来剪枝，发现不可行。

T3 写完暴力尝试把几个贪心拼起来：从根往下选，从父亲往上选，选 \(c\) 最小的，随机选，选父亲的答案（现在一想可以随机选根到父亲的答案），根据时空限制调了调参数，大概 17.00 丢下。

T1 又尝试了维护右凸包、类似平面图转对偶图的建图（可惜当时一直想从左到右跑最短路，没有考虑从上到下），还是老老实实二分吧。check 时枚举每个点，看上下会不会形成“屏障”（能不能走通），同样没想到从上边界往下边界搜。

最后剩 5min 才开始交题，网站还卡了，以后要早点。感觉自己考得很差，很慌。

res

spj 和数据上出大锅了，导致 T3 有一堆人爆 \(0\)（包括我，因此 rk10+），机房里高声赞美出题人。没想到晚饭后 T3 修复 spj 重测了。

rk3 40+20+50

T1 WA了一个点，首先是算距离是平方爆 int 了，其次屏障不一定长得是从上到下，可能会“拐弯”。\(O(k^2\log\frac m\epsilon)\) 能拿 80pts

T3 一分都没有骗到。。。

rk1 杨卓凡 80+20+30

rk3 赵思远 10+20+80

rk5 彭乙桐 10+40+50

题解

说实话，官方和大部分网上的题解都质量低下，写得很含糊，代码也没有注释，但这套题不论是思维还是代码都很好，这里详细写一下题解。

Star Way To Heaven

80pts 做法

把上下边界也看作两点。

有两种理解：

1. 点集的每个子集都会构成一个屏障，显然每个屏障选择穿过最长的边，答案即为所有最长边的最小值。考虑直接求出最小的屏障，那么从上边界开始，每次把距离当前点集最近的点加入点集，下边界被加入点集时结束。发现这个算法就是 Prim
2. 相当于求从上边界到下边界的最小瓶颈路，Prim 求 MST

code

const int N = 6005;
int n,m,k;
double x[N],y[N];

double ans,d[N];
bool vis[N];

double dis(int i,int j)
	{ return sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j])); }

signed main() {
	scanf("%d%d%d",&n,&m,&k);
	For(i,1,k) scanf("%lf%lf",&x[i],&y[i]), d[i] = m-y[i];
	d[0] = 2e9, d[k+1] = m;
	for(;;) {
		int u = 0;
		For(i,1,k+1) if( !vis[i] && d[i] < d[u] ) u = i;
		vis[u] = 1, ans = max(ans,d[u]);
		if( u == k+1 ) break;
		For(i,1,k) d[i] = min(d[i],dis(u,i));
		d[k+1] = min(d[k+1],y[u]);
	}
	printf("%.8lf",ans/2);
	return 0;
}

God Knows

考虑 DP。设 \(f[i]\) 为选 \((i,p[i])\) 且前 \(i\) 个点的连线均已删的最小代价，转移时枚举 \(j\in[0,i)\)，要求 \(i,j\) 之间的连线与 \((i,p[i])\) 或 \((j,p[j])\) 相交：

\[f[i]=min(f[i],f[j]+c[i]),\forall k\in(j,i)\ ,p[k]<p[j]或p[k]>p[i]
\]

下文代码是 \(O(n^3)\) 的，但通过预处理可以优化到 \(O(n^2)\)。

40pts

const int N = 2e5+5;
int n,p[N],c[N];

int f[N],ans=0x3f3f3f3f;

bool check(int l,int r) {
	if( p[l] > p[r] ) return 0;
	For(i,l,r) if( p[l] < p[i] && p[i] < p[r] ) return 0;
	return 1;
}

signed main() {
	read(n);
	For(i,1,n) read(p[i]);
	For(i,1,n) read(c[i]);
	mem(f,0x3f,n);
	f[0] = 0;
	For(i,1,n) For(j,0,i-1)
		if( check(j,i) ) f[i] = min(f[i],f[j]+c[i]);
	for(int i = n, j = 0; i && p[i] >= p[j]; --i) {
		ans = min(ans,f[i]);
		j = max(j,p[i]);
	}
	write(ans);
	return ioclear();
}

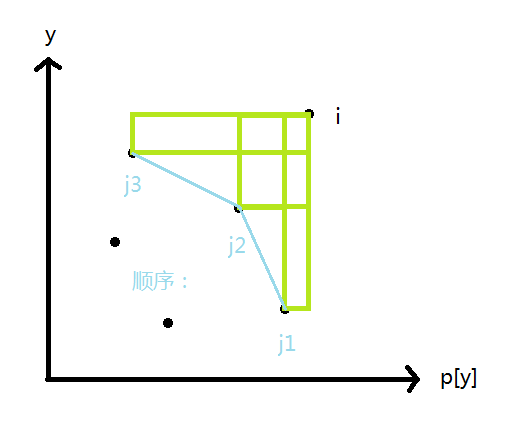
把 \((i,p[i])\) 看作二维坐标系中的点，考虑转移方程中条件的几何意义：以 \((i,p[i]),(j,p[j])\) 为对角的矩形中没有其他点（合法的 \(j\) 构成了右半个上凸包）。尝试用数据结构求 \(\min\{f[j]\}\)，但条件中 \(p[k]\) 有两种合法情况很烦，考虑交换 \(x,y\) 坐标。以 \(p\) 为下标建线段树，以 \(p\) 递减的顺序查询，那么 \(j\) 应递增（从右往左查这个 \(\frac 14\) 凸包）。写法类似李超线段树，时间复杂度 \(O(n\log^2n)\)。

100pts

const int N = 2e5+5, inf = 0x3f3f3f3f;
int n,p[N];

int res,now; // now: 当前的j。左边的j要大于它
struct Node {
	int l,r,mx,lmn,f;
	// mx: 最大的i;
	// lmn: 预处理左半区间的答案（插入变为\log^2n，否则calc会变成n\logn）
} t[N*4];

#define ls (u<<1)
#define rs (u<<1|1)
void build(int u,int l,int r) {
	t[u].l = l, t[u].r = r, t[u].lmn = inf;
	if( l == r ) return;
	int mid = l+r>>1;
	build(ls,l,mid), build(rs,mid+1,r);
}
int calc(int u,int qr) { // 求t[u].l<=p[j]<=t[u].r,j>qr的min{f[j]}
	if( t[u].l == t[u].r ) return t[u].mx > qr ? t[u].f : inf;
	if( t[rs].mx >= qr ) return min(t[u].lmn,calc(rs,qr));
	return calc(ls,qr);
}
void insert(int u,int x,int y,int f) { // (p[i]=x,i=y),f[i]=f
	if( t[u].l == t[u].r ) { t[u].mx = y, t[u].f = f; return; }
	insert( x<=t[ls].r?ls:rs ,x,y,f);
	t[u].mx = max(t[ls].mx,t[rs].mx), t[u].lmn = calc(ls,t[rs].mx);
}
void query(int u,int x) {
	if( t[u].r <= x ) {
		res = min(res,calc(u,now)), now = max(now,t[u].mx);
		return;
	}
	if( t[rs].l <= x ) query(rs,x);
	query(ls,x); // 顺序不能反
}

signed main() {
	read(n);
	For(i,1,n) read(p[i]);
	build(1,1,n);
	For(i,1,n) {
		int c; read(c);
		res = inf, now = 0, query(1,p[i]);
		insert(1,p[i],i,(res==inf?0:res)+c);
	}
	res = inf, now = 0, query(1,n);
	write(res);
	return ioclear();
}

对代码的解释可以看 ys的博客

Lost My Music

把式子化成

\[-\frac{c[u]-c[v]}{dep[u]-dep[v]}
\]

那么把每个点看作二维坐标系上 \((dep[i],c[i])\)，忽略负号的话就是求斜率的最大值，维护下凸包

写法有两种：

一种是倍增，设 \(f[u][0]\) 为 \(u\) 的祖先中，下凸包上 \(u\) 的前一个点。

另一种是单调栈上二分，用到了树上还原栈的技巧。

倍增

const int N = 5e5+5;
int n,c[N],fa[N];
vector<int> to[N];

int dep[N],f[N][19];

LD K(int u,int v) { return LD(c[u]-c[v])/(dep[u]-dep[v]); }

void dfs(int u) {
	dep[u] = dep[fa[u]] + 1;
	int p = fa[u];
	rFor(i,17,0) if( f[p][i] > 1 )
		if( K(f[f[p][i]][0],f[p][i]) > K(f[p][i],u) ) p = f[p][i];
	if( p != 1 && K(f[p][0],u) > K(p,u) ) p = f[p][0];
	f[u][0] = p;
	For(i,1,18) f[u][i] = f[f[u][i-1]][i-1];
	for(int v : to[u]) dfs(v);
}

signed main() {
	read(n);
	For(i,1,n) read(c[i]);
	For(i,2,n) read(fa[i]), to[fa[i]].pb(i);
	dfs(1);
	For(i,2,n) printf("%.10Lf\n",-K(f[i][0],i));
	return ioclear();
}

二分 by hkh

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1100000;
long double ans[N];
int dep[N],head[N],cnt,zhan[N];
int n;
ll c[N];
struct bian
{
	int nxt,to;
}b[N];
void add(int u,int v)
{
	b[++cnt].to=v;
	b[cnt].nxt=head[u];
	head[u]=cnt;
}
long double K(int x,int y)
{
	return (long double)(c[x]-c[y])/(long double)(dep[x]-dep[y]);
}
int get(int u,int r)
{
	int l=2,mid;
	long double k1,k2;
	while(l<=r)
	{
		mid=(l+r)>>1;
		k1=(long double)(-1)*K(zhan[mid],zhan[mid-1]);
		k2=(long double)(-1)*K(zhan[mid],u);
		if(k1<k2)
			r=mid-1;
		else
			l=mid+1;
	}
	return l-1;
}
void dfs(int u,int fa,int top)
{
	int k=get(u,top)+1,tmp1=zhan[k],tmp2=zhan[k-1];
	if(u==1)
		k=1;
	ans[u]=(long double)(-1)*K(tmp2,u);
	zhan[k]=u;
	for(int i=head[u],v;i;i=b[i].nxt)
	{
		v=b[i].to;
		if(v==fa)
			continue;
		dep[v]=dep[u]+1;
		dfs(v,u,k);
	}
	zhan[k]=tmp1;
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%lld",&c[i]);
	}
	for(int i=2,a;i<=n;i++)
	{
		scanf("%d",&a);
		add(a,i);
	}
	dep[1]=1;
	dfs(1,0,0);
	for(int i=2;i<=n;i++)
	{
		printf("%.10Lf\n",ans[i]);
	}
	return 0;
}