SLAM的数学基础（3）：几种常见的概率分布的实现及验证。

分布，在计算机学科里一般是指概率分布，是概率论的基本概念之一。分布反映的是随机或某个系统中的某个变量，它的取值的范围和规律。

常见的分布有：二项分布、泊松分布、正态分布、指数分布等，下面对它们进行一一介绍。

PS：本文中谈到的PDF、PMF、CDF均为公认的缩写方式：

PDF：概率密度函数（probability density function）；

PMF：概率质量函数（probability mass function）；

CDF：累积分布函数（cumulative distribution function）。

二项分布

说起二项分布，离不开伯努利实验，二项分布就是重复N次的伯努利实验（伯努利实验，是指一种只有两种相反结果的随机试验，比如抛硬币，结果只有正面和反面；又比如投篮，只有投中和没有投中两种结果）。它的PMF可写作：

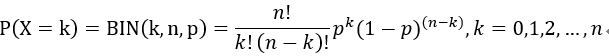
其中k为在n次实验中命中的次数，成功的概率为p。

二项分布的CDF可以写作：

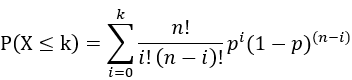
例子：抛10次硬币，有2次正面朝上的概率是多少？下面分别用C++实现和用numpy证明结果

C++实现：

#include <vector>
#include <iostream>
#include <iomanip>

double calc_binomial(int n, int k, double p)
{
  if(n < 0 || k < 0)
    return 0.0;

  std::vector< std::vector< double > > binomials((n + 1), std::vector< double >(k + 1));

  binomials[0][0] = 1.0;

  for(int i = 1; i < (n + 1); ++i)
    binomials[i][0] = (1.0 - p) * binomials[i - 1][0];
  for(int j = 1; j < (k + 1); ++j)
    binomials[0][j] = 0.0;

  for(int i = 1; i < (n + 1); ++i)
    for (int j = 1; j < (k + 1); ++j)
      binomials[i][j] = (1.0 - p) * binomials[i - 1][j] + p * binomials[i - 1][j - 1];
  return binomials[n][k];
}

int main()
{
  std::cout << std::fixed << std::setprecision(8) << calc_binomial(10, 2, 0.50) << std::endl;
}

结果为：0.04394531

Python实现：

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

def calc_binomial():
    n = 10
    p = 0.5
    k = 2
    binomial = stats.binom.pmf(k,n,p)
    print binomial

calc_binomial()

结果为：0.0439453125

反之，知道投10次硬币朝上的平均概率为0.3（即平均有3次朝上），试着从10000次实验中找出规律。

用C++实现：

#include <iostream>
#include <cmath>
#include <iomanip>
#include <vector>
#include <cstdlib>
#include <ctime>

int gen_binomial_rand(int n, double p)
{
  int k = 0;

  for(int i = 0; i < n; i++)
  {
    double current_probability = ((double)rand() / (double)RAND_MAX);
    if(current_probability < p)
    {
      k++;
    }
  }

  return k;
}

int main()
{
  srand((unsigned)time(NULL));

  int gn = 10;
  double gp = 0.3;
  int times = 10000;
  int sum_of_times = 0;

  std::vector< int > result(gn);

  for(int t = 0; t < times; t++)
  {
    int single_result = gen_binomial_rand(gn, gp);
    if(single_result < gn)
    {
      result[single_result]++;
    }
  }

  std::cout << std::endl;
  for(int i = 0; i < gn; i++)
  {
    sum_of_times += result[i];
    std::cout << result[i] << ",";
  }
  std::cout << std::endl;

  std::cout << "Total: " << sum_of_times << std::endl;

  return 0;
}

结果为：

323,1199,2310,2631,1951,1103,367,97,18,1,
Total: 10000

拿到Python里面用图表看一下：

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

def show_binom_rvs():
    n = np.array([323,1199,2310,2631,1951,1103,367,97,18,1])
    plt.plot(n)
    plt.show()
show_binom_rvs()

显示为：

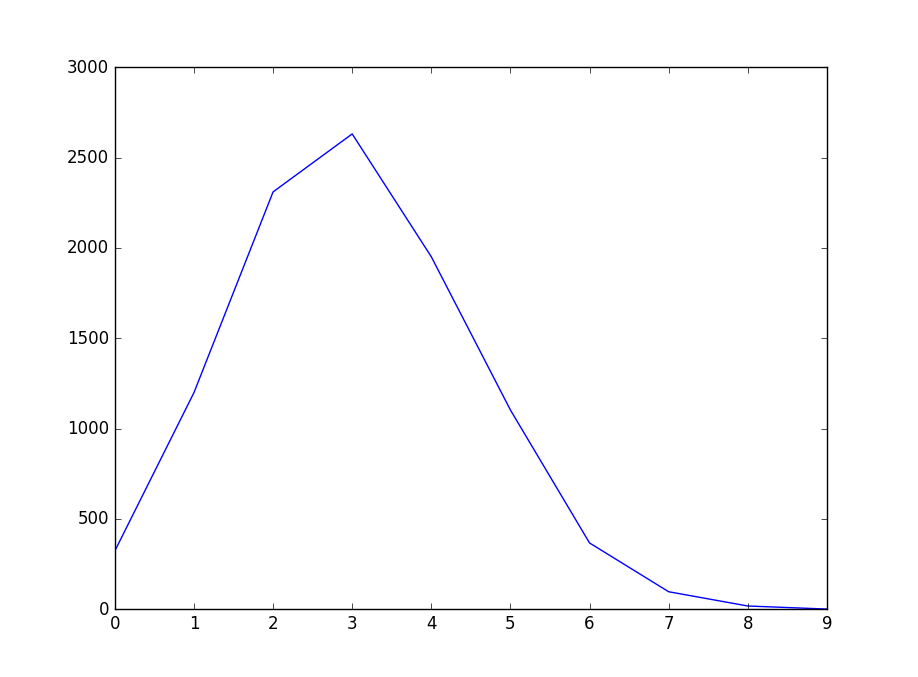
我们再来用Python的numpy和scipy的库来验证一下：

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

def calc_binom_rvs():
    binom_rvs = stats.binom.rvs(n=10,p=0.3,size=10000)
    plt.hist(binom_rvs, bins=10)
    plt.show()

calc_binom_rvs()

得到结果图片：

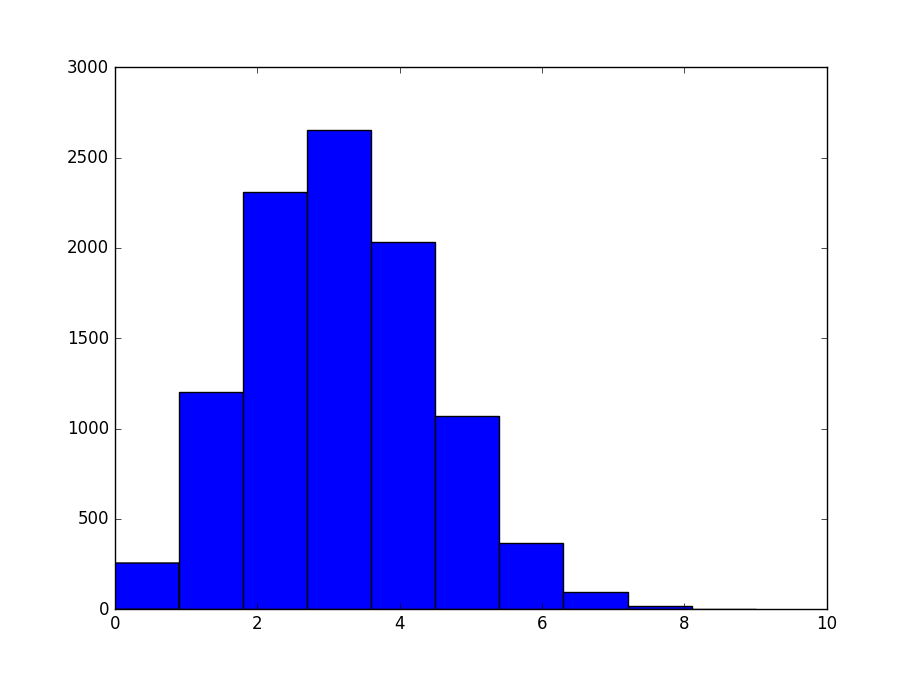
可以看到两次的图形包络是近似的。

泊松分布

在日常生活中，我们经常会遇到一些事情，这些事情发生的频率比较固定，但是发生的时间是不固定的，泊松分布就是用来描述单位时间内随机事件的发生概率。比如：知道一个医院平均每小时有3个小孩出生，那么下一个小时出生2个小孩的概率是多少？

泊松分布的PMF可以写作：

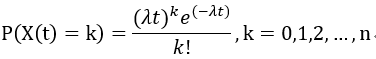
其中，t为连续时间长度，k为事件发生的次数，λ为发生事件的数学期望（如单位时间内发生事件的均值），e为自然底数。

就上面的例子，知道一个医院平均每小时有3个小孩出生，那么下一个小时出生2个小孩的概率是多少？用C++实现：

#include <iostream>
#include <cmath>
#include <iomanip>

double calc_poisson(int k, int lambda)
{
  double result;

  result = pow(lambda, k) * exp(-lambda);

  int factorial = 1;

  for(int i = 1; i <= k; i++)
  {
    factorial *= i;
  }

  result = result / factorial;

  return result;
}

int main()
{
  std::cout << std::fixed << std::setprecision(8) << calc_poisson(2, 3) << std::endl;
}

结果是：0.22404181

用Python验证：

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

def calc_poisson():

    lambd = 3
    k = 2
    y = stats.poisson.pmf(k,lambd)
    print y

calc_poisson()

结果是：0.224041807655

下面再用C++实现生成泊松随机数，并用Python检验：

C++实现：

#include <iostream>
#include <cmath>
#include <iomanip>
#include <vector>
#include <cstdlib>
#include <ctime>

double binary_random()
{
  double rand_number = (rand() % 100);
  rand_number /= 100;
  return rand_number;
}

int calc_poisson(int lambda)
{
  int k = 0;
  double p = 1.0;
  double l = exp(-lambda);

while(p >= l)
  {
    double r = binary_random();
    p *= r;
    k++;
  }
 
  return (k - 1);
}

int main()
{
  int t = 10000;
  int lambda = 3;
  int distribution = 20;
  int dist_cells[distribution] = {0};

srand((unsigned)time(NULL));

for(int i = 0; i < t; i++)
  {
    int n = calc_poisson(lambda);
    dist_cells[n]++;
  }

for(int i = 0; i < distribution; i++)
  {
    std::cout << dist_cells[i] << ",";
  }
  std::cout << std::endl;
 
 
  return 0;
}

运行结果为：467,1604,2298,2264,1608,952,466,217,87,29,6,2,0,0,0,0,0,0,0,0,

放入Python显示并和Python生成的比较：

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

def gen_poisson_rvs():
    dist = 20
    cpp_result = np.array([467,1604,2298,2264,1608,952,466,217,87,29,6,2,0,0,0,0,0,0,0,0])
    py_result = np.random.poisson(lam=3,size=10000)

    plt.hist(py_result,bins=dist,range=[0,dist],color='g')
    plt.plot(cpp_result,color='r')
    plt.show()

gen_poisson_rvs()

运行并显示图表为：

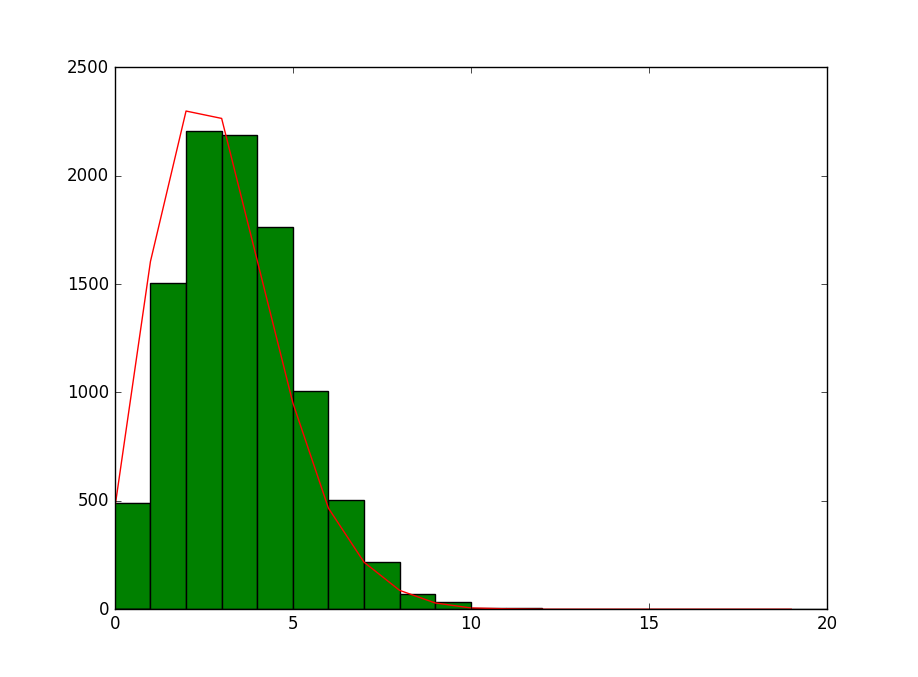
指数分布

指数分布，描述的是在某一事件发生后，在连续时间间隔内继续发生的概率。比如上面的例子，知道一个医院平均每小时有3个小孩出生，刚刚已经有一个小孩出生了，那么下一个小孩在15分钟内出生的概率是多少？

指数分布的CDF可以写作：

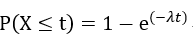
其中t为时间长度，e为自然底数。

下面用C++实现：

#include <iostream>
#include <cmath>
#include <iomanip>

double calc_exponential(double lambda, double t)
{
  double result;

  result = (1 - exp((-lambda) * t));

  return result;
}

int main()
{
  std::cout << std::fixed << std::setprecision(8) << calc_exponential(3, 0.25) << std::endl;
}

结果为：0.52763345

用Python验证：

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

def calc_expon():
    lambd = 3
    x = np.arange(0,1,0.25)
    y = 1 - np.exp(-lambd *x)
    print y

calc_expon()

结果为：[ 0.          0.52763345  0.77686984  0.89460078]

其中x=0.25时结果为0.52763345

下面是生成lambda=3的指数分布随机数，样本数是10000。同样是用C++实现，Python验证。

C++实现：

#include <iostream>
#include <cmath>
#include <iomanip>
#include <vector>
#include <cstdlib>
#include <ctime>

double calc_exponential(double lambda)
{
  double expon_rand = 0.0;
  while(1)
  {
    expon_rand = ((double)rand()/(double)RAND_MAX);
    if(expon_rand != 1)
    {
      break;
    }
  }
  expon_rand = ((-1 / lambda) * log(1 - expon_rand));
  return expon_rand;
}

int main()
{
  int t = 10000;
  double lambda = 3;
  const int distribution = 20;
  double dist_cells[distribution] = {0};

  srand((unsigned)time(NULL));

  for(int i = 0; i < t; i++)
  {
    int n = calc_exponential(lambda);
    dist_cells[n]++;
  }

  for(int i = 0; i < distribution; i++)
  {
    std::cout << dist_cells[i] << ",";
  }
  std::cout << std::endl;

  return 0;
}

结果是：9515,469,16,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,

放入Python并用Python生成的对比：

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

def gen_expon_rvs():
    cpp_result = np.array([9515,469,16,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0])

    lambd_recip = 0.33
    py_result = stats.expon.rvs(scale=lambd_recip,size=10000)
    plt.plot(cpp_result,color='r')
    plt.hist(py_result,color='b')
    plt.xlim(0,20)
    plt.show()

gen_expon_rvs()

得到图片：

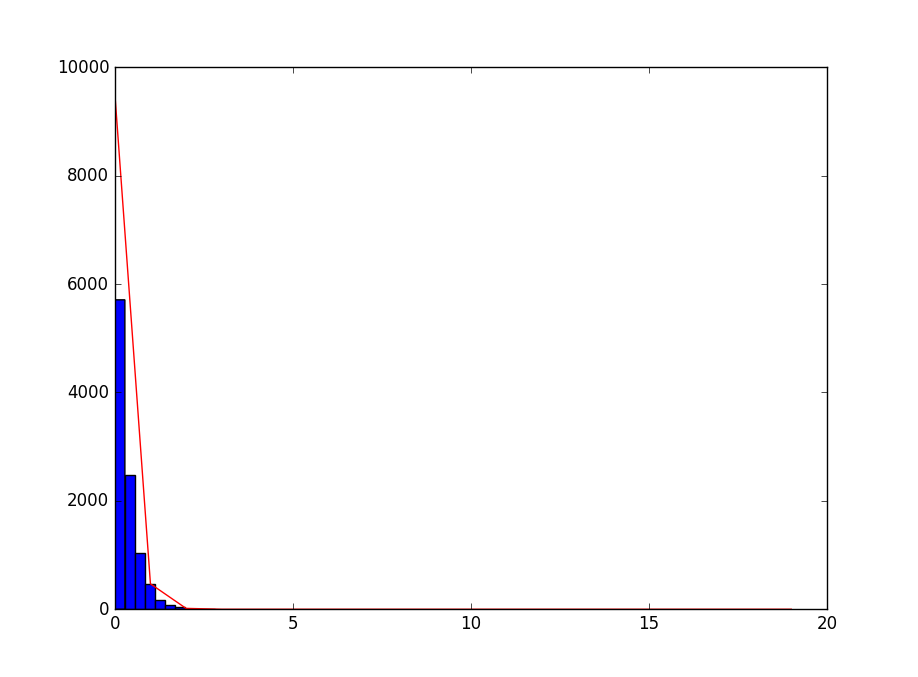
PS：其中最大值不一致的情形并不是计算错误，而是X轴的分布单位不一致，Python的是浮点的，而C++的代码是整形的，所以看到Python的分布最大值比较小是因为平均到了小数。

正态分布（高斯分布）

翻开任何一本讲统计的数学书，对于正态分布大抵会有相似的描述：若一个随机变量X服从一个数学期望为λ，标准差为σ的概率分布，且PDF为：

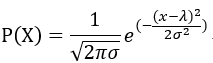
则称这个随机变量为正态随机变量。

当λ=0，σ=1时，称其为标准正态分布，PDF简化为：

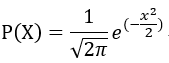
在现实中，有大量的案例是符合正态分布的，比如全中国18岁以上男性人口的身高分布，170cm左右的占绝大部分，160和180的占较少部分，150以下和190以上的占极少部分。

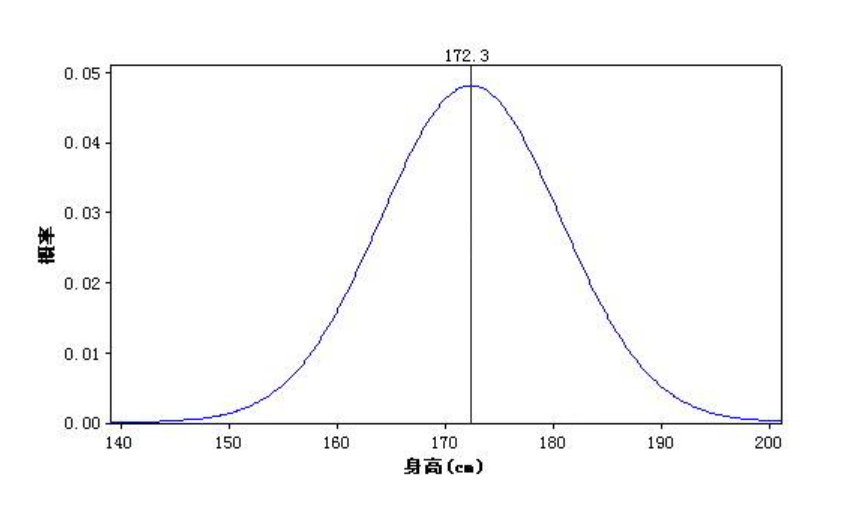
说起正态分布的例子，有个著名的实验是不得不提的，那就是高尔顿钉板实验。

高尔顿钉板是在一块竖起的木板上钉上一排排互相平行、水平间隔相等的铁钉，并且每一排钉子数目都比上一排多一个，一排中各个钉子下好对准上面一排两上相邻铁钉的正中央。从入口处放入一个直径略小于两颗钉子间隔的小球，当小球从两钉之间的间隙下落时，由于碰到下一排铁钉，它将以相等的可能性向左或向右落下，接着小球再通过两钉的间隙，又碰到下一排铁休。如此继续下去，小球最后落入下方条状的格子内。在等可能性（即小球落在左边和落在右边的概率均为50%）的情况下，小球落下后满足正态分布。

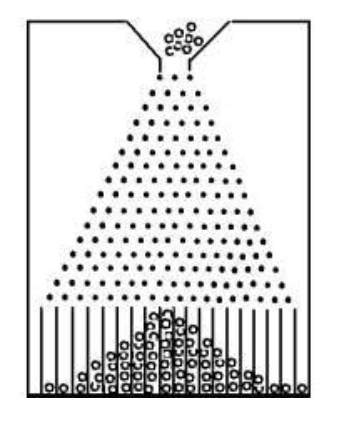
下面的代码用C++计算模拟高尔顿实验过程，并把结果放到Python显示出来。

C++模拟实验过程：

#include <iostream>
#include <cmath>
#include <iomanip>
#include <vector>
#include <cstdlib>
#include <ctime>

int binary_random()
{
  double rand_number = (rand() / (double)RAND_MAX);
  if(rand_number > 0.5)
    return 1;
  else return 0;
}

void galton_test(int num_of_cells, int num_of_balls)
{
  srand((unsigned)time(NULL));

  std::vector< int > cells(num_of_cells);

  int rand;

  for(int i = 1; i <= num_of_balls; i++)
  {
    int cell = 0;
    for(int j = 1; j < num_of_cells; j++)
    {
      int rand = binary_random();
      cell += rand;
    }
    cells[cell]++;
  }

  std::cout << std::endl;
  for(int i = 0; i < num_of_cells; i++)
  {
    std::cout << cells[i] << ",";
  }
  std::cout << std::endl;
}

int main()
{
  galton_test(20, 5000);
}

结果为：0,0,3,14,45,95,264,481,720,886,911,741,452,240,95,45,6,1,1,0,

结果每次都不一样，但将其放入以下Python代码显示：

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

def show_galton():
    n = np.array([0,0,3,14,45,95,264,481,720,886,911,741,452,240,95,45,6,1,1,0])

    plt.plot(n)

    plt.show()

show_galton()

得到以下图片：

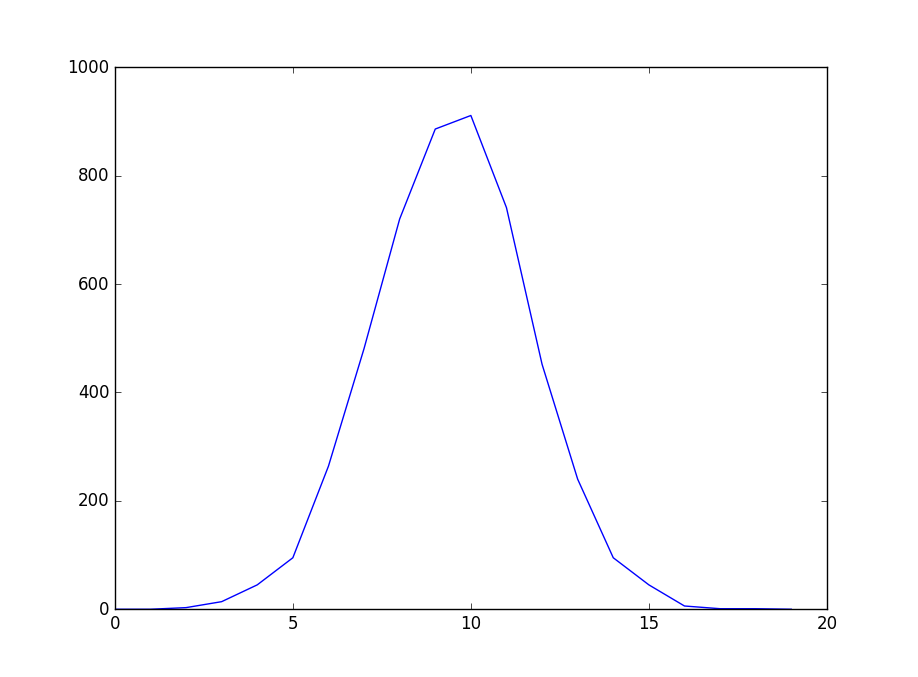
可以看出，是个明显的钟型曲线，说明高尔顿实验是满足正态分布的。在这个实验中，我们还可以去调整num_of_cells, num_of_balls的值，可以看出，当num_of_cells的值越大，曲线越陡峭，越小，曲线越平坦；num_of_balls的值越大，曲线就越像正态分布。说到这里可能大家就会想的到，这个实验中，num_of_cells的值可以认为就是正态分布的σ，而我们设定的随机数0，1会影响到正态分布的λ，有兴趣的朋友可以改一下上面的例程，将随机数生成改为大于0.5，或小于0.5，可以观察到最后的曲线中轴线会向左偏和向右偏。

说到这里，下面的公式应该是理所当然的了：

若一个随机变量X服从一个数学期望为λ，尺度参数为σ的概率分布，记作

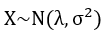
说到这里，通过上面的实验大家应该大概知道高斯分布是个什么东西了。那么如何编程实现生成符合高斯分布的随机数呢？

生成高斯分布的随机数有多种方法：

（1）     Box-Muller变换算法

（2）     利用中心极限定理迭代法

（3）     Ziggurat算法

等。其中，在效率和通用性方面比较均衡的是Box-Muller算法，C++11和Python的数学库里面基本都是用的它。

它的原理是：

随机抽出从[0,1]中符合均匀分布的数a和b，然后令：

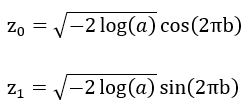
那么这两个数都是符合正态分布的。

若想产生服从期望是λ，标准差是σ的正态分布，那么：

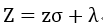
下面，我们用C++来实现：

#include <iostream>
#include <cmath>
#include <iomanip>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <limits>

double calc_gaussian(double sigma, double lambda)
{
  static const double epsilon = std::numeric_limits<double>::min();
  static const double two_pi = (2.0 * 3.14159265358979323846);

  static double z1;
  static bool generate;
  generate = !generate;

  if (!generate)
    return z1 * sigma + lambda;

  double a, b;
  do
  {
    a = rand() * (1.0 / RAND_MAX);
    b = rand() * (1.0 / RAND_MAX);
  }while ( a <= epsilon );

  double z0;
  z0 = sqrt(-2.0 * log(a)) * cos(two_pi * b);
  z1 = sqrt(-2.0 * log(a)) * sin(two_pi * b);
  return z0 * sigma + lambda;
}

int main()
{
  int t = 10000;
  double lambda = 10;
  double sigma = 1;
  const int distribution = 20;
  double dist_cells[distribution] = {0};

  srand((unsigned)time(NULL));

  for(int i = 0; i < t; i++)
  {
    int n = calc_gaussian(sigma, lambda);
    dist_cells[n]++;
  }

  for(int i = 0; i < distribution; i++)
  {
    std::cout << dist_cells[i] << ",";
  }
  std::cout << std::endl;

  return 0;
}

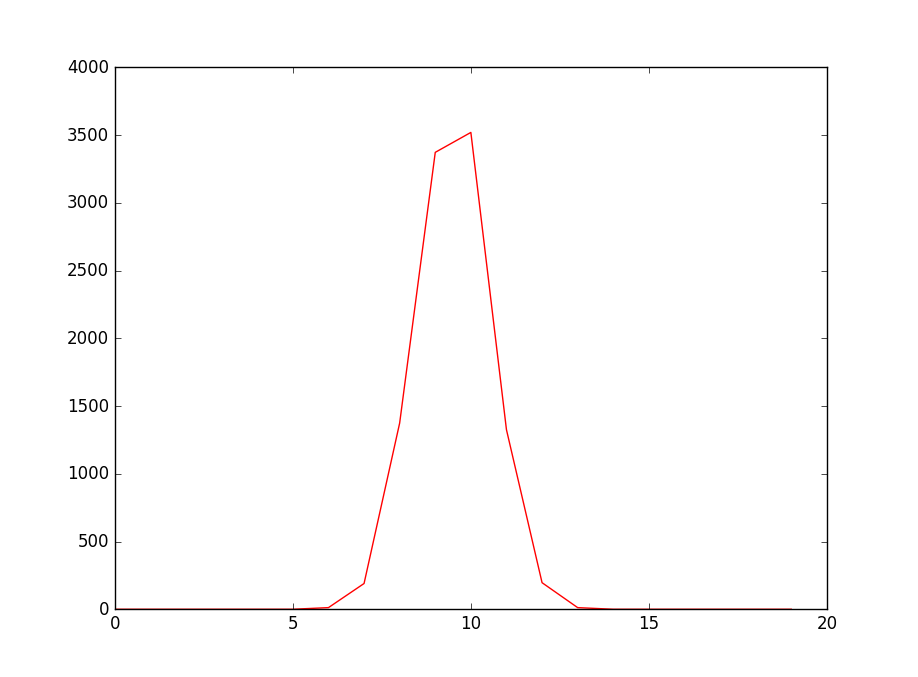
得到结果：0,0,0,0,0,0,12,190,1374,3372,3519,1325,196,12,0,0,0,0,0,0,

放入Python显示：