【递归+树】FBI树

题目描述

我们可以把由“0”和“1”组成的字符串分为三类：全“0”串称为BB串，全“1”串称为I串，既含“0”又含“1”的串则称为F串。

FBI树是一种二叉树，它的结点类型也包括FF结点，B结点和I结点三种。由一个长度为2^N的“01”串S可以构造出一棵FBI树T，递归的构造方法如下：

1. T的根结点为R，其类型与串S的类型相同；
2. 若串S的长度大于1，将串S从中间分开，分为等长的左右子串S1和S2;由左子串S1构造R的左子树\(T_1\) ，由右子串\(S_2\)构造\(R\)的右子树\(T_2\)。
   
   现在给定一个长度为2^N的“0101”串，请用上述构造方法构造出一棵FBI树，并输出它的后序遍历序列。

分析

2004年的NOIP第三题，还是比较水的，但毕竟是考题还是要重点讲解一下。

可以理解成二分，其实题意上也就是这样理解的，那么将首先是对这个序列进行遍历



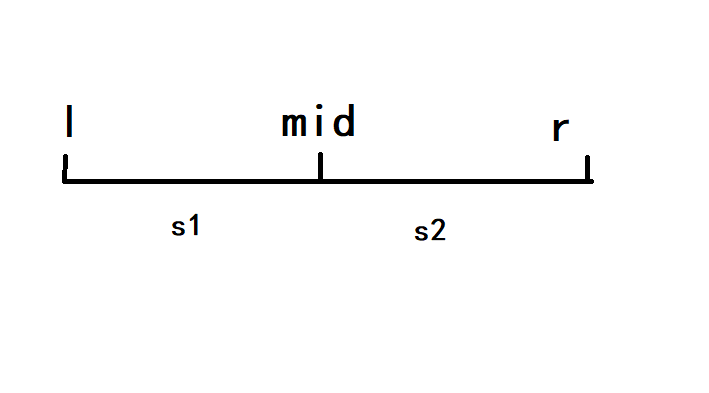
也就是上图的方式，非常好理解。

接下来的思路就是二分对这个序列进行solve，那么首先对这个序列进行二分，二分的边界条件就是指针\(l\)和指针\(r\)相撞在一起，此时说明当前序列中已经没有数存在了。

那么接下来是对当前已经二分过的序列进行统计当前的0和1的个数。根据题意输出。

如果只是这样输出，在调试的时候可以发现答案是对的，但是我们要考虑一个问题：为什么这个答案是对的？

也就是为什么我们输出的答案就是它的后序遍历。答案很简单，因为我们是进行的是（solve(l,mid)和solve(mid+1,r)）的过程，所以我们首先会遍历到的就是最左边的叶节点。那么我们采用递归的方法，所以这个节点的father一定是在当前节点之前遍历到的，所以我们的答案正确性就可以保证了。

AC代码

#include <bits/stdc++.h>
using namespace std;
#define ms(a,b) memset(a,b,sizeof(a))
typedef long long ll;
const int maxn=1<<10;
int n;
char st[maxn];
inline int read(){
    int X=0,w=0; char ch=0;
    while(!isdigit(ch)) {w|=ch=='-';ch=getchar();}
    while(isdigit(ch)) X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
    return w?-X:X;
}
void solve(int l,int r) {
    int mid((l+r)>>1);
    if (l!=r) solve(l,mid),solve(mid+1,r);
    int cnta=0,cntb=0;
    for (int i=l;i<=r;i++) {
        if (st[i]=='0') cnta++;
        else cntb++;
    }
    if (cnta&&cntb) printf("F");
    else if (cnta) printf("B");
    else printf("I");
}
int main(int argc,char* argv[]){
    n=read();
    scanf("%s",st+1);
    solve(1,1<<n);
	return 0;
}