《University Calculus》-chaper13-多重积分-二重积分的计算

之前关于二重积分的笔记，介绍了二重积分概念的引入，但是对于它的计算方法(化为累次积分)，介绍的较为模糊，它在《概率论基础教程》中一系列的推导中发挥着很重要的作用。

回想先前关于二重积分的几何含义，求解一个曲顶圆柱的体积，我们用如下的符号进行定义：

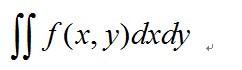
现在我们通过另外一条路径，再次得到几何体的体积，便可以建立等式，那么对于一般的二重积分，我们就找到了计算方法。

看这样一个图：

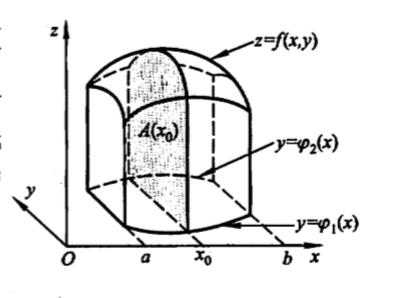
落在x-O-y上的面积就是被积区域D，几何体的顶部z=f(x,y)就是被积函数，为了求解这个几何体的体积，我们采取先求侧面面积(平行于y-O-z面)，然后对基于所求结果再对x进行积分，便得到了几何体的体积。

侧面积A(x0)：

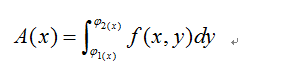
简单的一维积分求解曲边梯形。

随后基于这个侧面积的结果再对x积分，显然就得到了体积，等式如下。

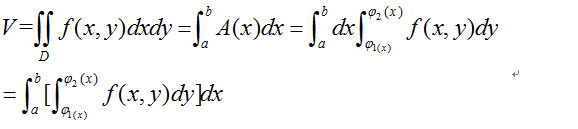
那么我们就将重积分化为了累次积分，在上述形式中，最后两个等号后边的形式都表示先对y积分然后对x积分。

需要注意，按照这种极限法表示几何的体积，对它的底面是有限制的，它分为X型积分区域和Y型积分区域，例如在上面的图中，是一个X型积分区域。

Y型积分区域：

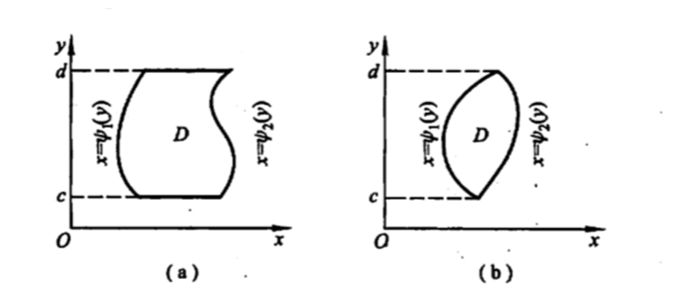
X型积分区域：

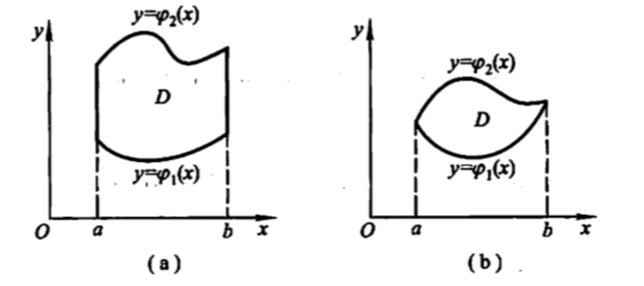
那么很显然，如果对于某个积分区域既满足X型又满足Y型，那么我们有如下的等式成立：

这个定理其实就是傅比尼定理增强形式，它是二重积分算法的基础，同时也是等价交换积分次序的基础。

这两种情况其实就是呼应着上面的X型和Y型积分区域，当某种情况既是X型积分区域又是Y型积分区域，那么便可以根据积分计算的便捷性进行积分次序的交换，而如果既不是X型也不是Y型，则考虑通过分割法将被积区域R变为X型与Y型的加和。其正确性结合上文关于二重积分几何意义的算法过程，是不言自明的。