BZOJ 1005 [HNOI2008]明明的烦恼 purfer序列,排列组合
1005: [HNOI2008]明明的烦恼
Description
自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在
任意两点间连线,可产生多少棵度数满足要求的树?
Input
第一行为N(0 < N < = 1000),
接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1
Output
一个整数,表示不同的满足要求的树的个数,无解输出0
Sample Input
1
-1
-1
Sample Output
HINT
两棵树分别为1-2-3;1-3-2
Source
题解:
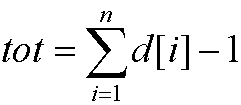
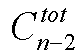 种插法;
种插法;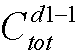 种插法;
种插法;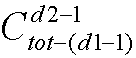 种插法;
种插法;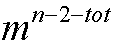 ;
;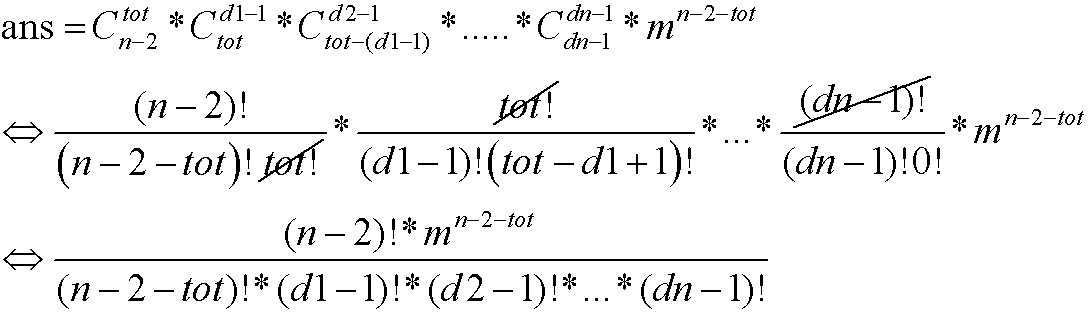
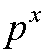 ,其中
,其中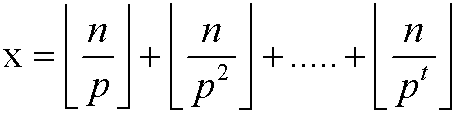 且
且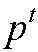 <n
<n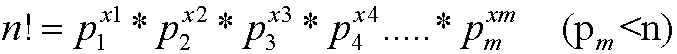
——转自怡红公子
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include<vector>
using namespace std;
const int N = 1e5+, M = 1e3+, mod = , inf = 1e9+;
typedef long long ll;
int n;
int d[N],ans[N];
int cnt[N],len=;
void go_way(int x,int key) {
for(int j=;j*j<=x;j++) {
while(x%j==) {
cnt[j]+=key;
x/=j;
// cout<<j<<endl;
}
}
cnt[x]+=key;
}
int sum = ,m;
void mul(int x)
{
for(int i=;i<=len;i++)
ans[i]*=x;
for(int i=;i<=len;i++)
{
ans[i+]+=ans[i]/mod;
ans[i]%=mod;
}
while(ans[len+]>)
{len++;ans[len+]+=ans[len]/mod;ans[len]%=mod;}
}
int main() {
scanf("%d",&n);
if(n==) {
int x;
scanf("%d",&x);
if(!x) cout<<;
else cout<<;
return ;
}
for(int i=;i<=n;i++) {
scanf("%d",&d[i]);
if(!d[i]) {cout<<;return ;}
if(d[i]==-) m++;
else {d[i]--;sum+=(d[i]);}
}
if(sum > n-) {
cout<<;
return ;
}
for(int i=;i<=n-;i++) go_way(i,);
for(int i=;i<=n--sum;i++) {
go_way(i,-);
}
for(int i=;i<=n;i++) {
if(d[i])
for(int j=;j<=d[i];j++) {
go_way(j,-);
}
}
ans[] = ;
for(int i=;i<=n;i++) {
for(int j=;j<=cnt[i];j++) mul(i);
}
for(int i=;i<=n--sum;i++) mul(m);
for(int i=len;i>=;i--)
if(i==len)printf("%d",ans[i]);
else printf("%06d",ans[i]);
return ;
}
BZOJ 1005 [HNOI2008]明明的烦恼 purfer序列,排列组合的更多相关文章
- BZOJ 1005: [HNOI2008]明明的烦恼 Purfer序列 大数
1005: [HNOI2008]明明的烦恼 Time Limit: 20 Sec Memory Limit: 256 MB 题目连接 http://www.lydsy.com/JudgeOnline/ ...
- BZOJ 1005 [HNOI2008] 明明的烦恼(组合数学 Purfer Sequence)
题目大意 自从明明学了树的结构,就对奇怪的树产生了兴趣...... 给出标号为 1 到 N 的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Input 第一行为 N( ...
- bzoj 1005: [HNOI2008]明明的烦恼 prufer编号&&生成树计数
1005: [HNOI2008]明明的烦恼 Time Limit: 1 Sec Memory Limit: 162 MBSubmit: 2248 Solved: 898[Submit][Statu ...
- BZOJ 1005 [HNOI2008]明明的烦恼 (Prufer编码 + 组合数学 + 高精度)
1005: [HNOI2008]明明的烦恼 Time Limit: 1 Sec Memory Limit: 162 MBSubmit: 5786 Solved: 2263[Submit][Stat ...
- BZOJ 1005: [HNOI2008]明明的烦恼( 组合数学 + 高精度 )
首先要知道一种prufer数列的东西...一个prufer数列和一颗树对应..然后树上一个点的度数-1是这个点在prufer数列中出现次数..这样就转成一个排列组合的问题了.算个可重集的排列数和组合数 ...
- bzoj 1005 [HNOI2008] 明明的烦恼 (prufer编码)
[HNOI2008]明明的烦恼 Time Limit: 1 Sec Memory Limit: 162 MBSubmit: 5907 Solved: 2305[Submit][Status][Di ...
- bzoj 1005: [HNOI2008]明明的烦恼 树的prufer序列+万进制
题目传送门 思路: 这道题需要前置知识prufer编码,这篇博客对prufer编码和这道题的分析写的很好. 这里主要讲一些对大数阶乘的分解,一个办法当然是用高精度,上面这篇博客用的是java,还有一个 ...
- BZOJ 1005: [HNOI2008]明明的烦恼(prufer数列)
http://www.lydsy.com/JudgeOnline/problem.php?id=1005 题意: Description 自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标 ...
- BZOJ.1005.[HNOI2008]明明的烦恼(Prufer 高精 排列组合)
题目链接 若点数确定那么ans = (n-2)!/[(d1-1)!(d2-1)!...(dn-1)!] 现在把那些不确定的点一起考虑(假设有m个),它们在Prufer序列中总出现数就是left=n-2 ...
随机推荐
- α&β测试的定义及结束的标准
α测试在系统开发接近完成时对应用系统的测试:测试后仍然会有少量的设计变更.这种测试一般由最终用户或其他人员完成,不能由程序或测试员完成. β测试当开发和测试根本完成时所做的用例,最终的错误和问题需要在 ...
- 【SQL】MERGE
MERGE可以合并多个表中的数据,也可实现多表中数据的同步.使用MERGE语句对表中数据进行有条件的更新和插入.当查找的行存在时,UPDATE更新行中的数据:当查找的行不存在时,INSERT插入数据. ...
- 解决Fiddler抓包上不了网的问题:
以前安装Fiddler 没有配置过相关设置,经常出现就是打开fiddler后,浏览器就无法上网了,刚开始觉得可能是因为而公司上网是需要自己的代理的,但fiddler打开后默认127.0.0.1作为IE ...
- Sobel算子取代:基于特定点方向的canny边缘检测
前言: Canny边缘检测使用了Sobel算子,计算dx和dy两个方向,对于特定方向的边缘检测,可以作少量修改. 代码: 计算特定方向上的边缘 void CannyOrient( cv::Mat &a ...
- 教材配套PPT初稿
1-10章初稿,基本完整.有些粗糙,后面可能会稍作调整. 附更新情况如下: 1.增加了第10章内容: 2.第5章增加了一些内容: 3.第3章内容部分更新: 4.增加了第8-9章内容. 订正:更新了第8 ...
- js取最值:
取最值是很常见的一种运算,各个语言都会遇到这个问题.Js中,如果简单的进行取最值,完全没必要自己写一个比较函数,原生的js就提供了方法.这些方法都属于Math 对象(引用w3c:Math 对象并不像 ...
- .NET Framework 3.5 安装
今天vCenter服务器悲剧了,只好火速重新部署新vCenter服务器... Windows server 2016 中,安装VCenter 5.5 提示 未安装 .NET Framework 3. ...
- BZOJ 1688: [Usaco2005 Open]Disease Manangement 疾病管理 状压DP + 二进制 + 骚操作
#include <bits/stdc++.h> #define setIO(s) freopen(s".in","r",stdin) #defin ...
- BZOJ 1572: [Usaco2009 Open]工作安排Job 贪心 + 堆 + 反悔
Description Farmer John想修理牧场栅栏的某些小段.为此,他需要N(1<=N<=20,000)块特定长度的木板,第i块木板的长度为Li(1<=Li<=50, ...
- 【剑指Offer】20、包含min函数的栈
题目描述: 定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1)). 解题思路: 使用两个stack,一个为数据栈,另一个为辅助栈.数据栈 ...
