Stanford机器学习---第五讲. 神经网络的学习 Neural Networks learning

原文 http://blog.csdn.net/abcjennifer/article/details/7758797

本栏目（Machine learning）包括单参数的线性回归、多参数的线性回归、Octave Tutorial、Logistic Regression、Regularization、神经网络、机器学习系统设计、SVM（Support Vector Machines 支持向量机）、聚类、降维、异常检测、大规模机器学习等章节。所有内容均来自Standford公开课machine learning中Andrew老师的讲解。（https://class.coursera.org/ml/class/index）

第五讲——Neural Networks 神经网络的表示

===============================

（一）、Cost function

（二）、Backpropagation algorithm

（三）、Backpropagation intuition

（四）、Implementation note: Unrolling parameters

（五）、Gradient checking

（六）、Random initialization

（七）、Putting it together

 

 

===============================

（一）、Cost function

 

假设神经网络的训练样本有m个，每个包含一组输入x和一组输出信号y，L表示神经网络层数，S_l表示每层的neuron个数(SL表示输出层神经元个数)。

将神经网络的分类定义为两种情况：二类分类和多类分类，

卐二类分类：S_L=1, y=0 or 1表示哪一类；

卐K类分类：S_L=K, y_i = 1表示分到第i类；（K>2）

我们在前几章中已经知道，Logistic hypothesis的Cost Function如下定义：

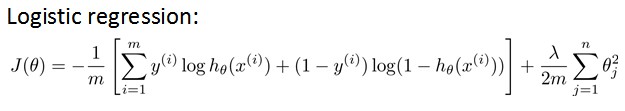
其中，前半部分表示hypothesis与真实值之间的距离，后半部分为对参数进行regularization的bias项，神经网络的cost function同理：

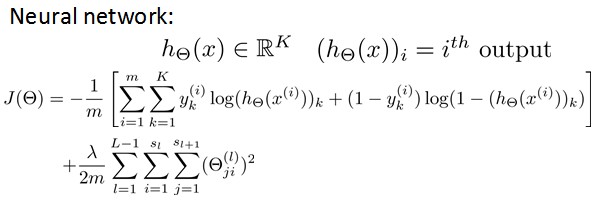
hypothesis与真实值之间的距离为 每个样本-每个类输出 的加和，对参数进行regularization的bias项处理所有参数的平方和

 

 

 

===============================

（二）、Backpropagation algorithm

前面我们已经讲了cost function的形式，下面我们需要的就是最小化J(Θ)

想要根据gradient descent的方法进行参数optimization，首先需要得到cost function和一些参数的表示。根据forward propagation,我们首先进行training dataset 在神经网络上的各层输出值：

我们定义神经网络的总误差为：

希望通过调整权重参数W（也就是theta）来最小化E。由于

所以每一层按如下方式进行更新：

根据backpropagation算法进行梯度的计算，这里引入了error变量δ，该残差表明了该节点对最终输出值的残差产生了多少影响。对于最后一层，我们可以直接算出网络产生的输出与实际值之间的差距，我们将这个差距定义为。对于隐藏单元我们如何处理呢？我们将通过计算各层节点残差的加权平均值计算hidden layer的残差。读者可以自己验证下，其实就是E对b求导的结果。

在最后一层中，

对于前面的每一层，都有

由此得到第l层第i个节点的残差计算方法：

由于我们的真实目的是计算,且

所以我们可以得到神经网络中权重的update方程：不断迭代直到落入local optima,就是backpropagation的算法过程。

============================================================Example of logistical cost:

下面我们针对logistical cost给出计算的例子：而对于每一层，其误差可以定义为：

分别代入即得

由此得来\theta_{k}的update方程：

 

如果将误差对激励函数（activation function）的导数记做δ，则有：

对于前面一层 ,更新同理，，只是上一层\Theta梯度的第一个分量E对a_k求导有所变化，

但是始终是不变的。

下图就是上面推导得出的结果：

由上图我们得到了error变量δ的计算，下面我们来看backpropagation算法的伪代码：

ps：最后一步之所以写+=而非直接赋值是把Δ看做了一个矩阵，每次在相应位置上做修改。

从后向前此计算每层依的δ，用Δ表示全局误差，每一层都对应一个Δ(l)。再引入D作为cost function对参数的求导结果。下图左边j是否等于0影响的是是否有最后的bias regularization项。左边是定义，右边可证明（比较繁琐）。

 

 

 

 

===============================

（三）、Backpropagation intuition

上面讲了backpropagation算法的步骤以及一些公式，在这一小节中我们讲一下最简单的back-propagation模型是怎样learning的。

首先根据forward propagation方法从前往后计算z^(j),a^(j) ;

然后将原cost function 进行简化，去掉下图中后面那项regularization项，

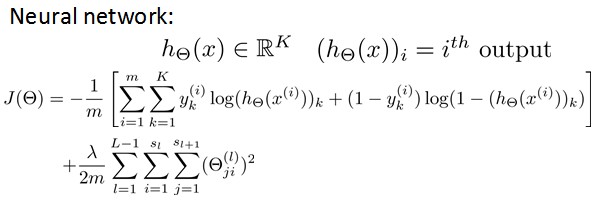
那么对于输入的第i个样本(xi,yi)，有

Cost(i)=y⁽ⁱ⁾log(h_θ(x⁽ⁱ⁾))+(1- y⁽ⁱ⁾)log(1- h_θ(x⁽ⁱ⁾))

由上文可知，

其中J就是cost。那么将其进行简化，暂时不考虑g'(zk) = ak(1-ak)的部分，就有：

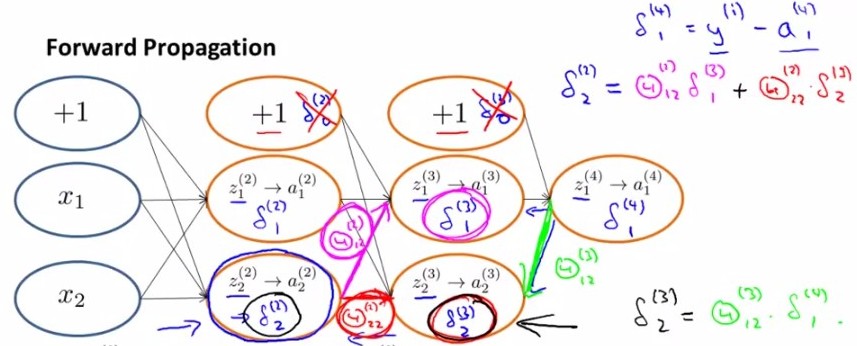
经过求导计算可得，对于上图有

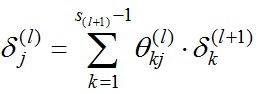
换句话说, 对于每一层来说，δ分量都等于后面一层所有的δ加权和，其中权值就是参数Θ。

 

 

 

===============================

(四)、Implementation note: Unrolling parameters

这一节讲述matlab中如何实现unrolling parameter。

前几章中已经讲过在matlab中利用梯度下降方法进行更新的根本，两个方程：

function [jVal, gradient] = costFunction(theta)

optTheta = fminunc(@costFunction, initialTheta, options)

与linear regression和logistic regression不同，在神经网络中，参数非常多，每一层j有一个参数向量Θj和Derivative向量Dj。那么我们首先将各层向量连起来，组成大vectorΘ和D，传入function，再在计算中进行下图中的reshape，分别取出进行计算。

计算时，方法如下：

 

 

===============================

（五）、Gradient checking

 

神经网络中计算起来数字千变万化难以掌握，那我们怎么知道它里头工作的对不对呢？不怕，我们有法宝，就是gradient checking，通过check梯度判断我们的code有没有问题，ok？怎么做呢，看下边：

对于下面这个【Θ-J(Θ)】图，取Θ点左右各一点（Θ+ε），（Θ-ε），则有点Θ的导数（梯度）近似等于(J（Θ+ε）-J（Θ-ε）)/(2ε)。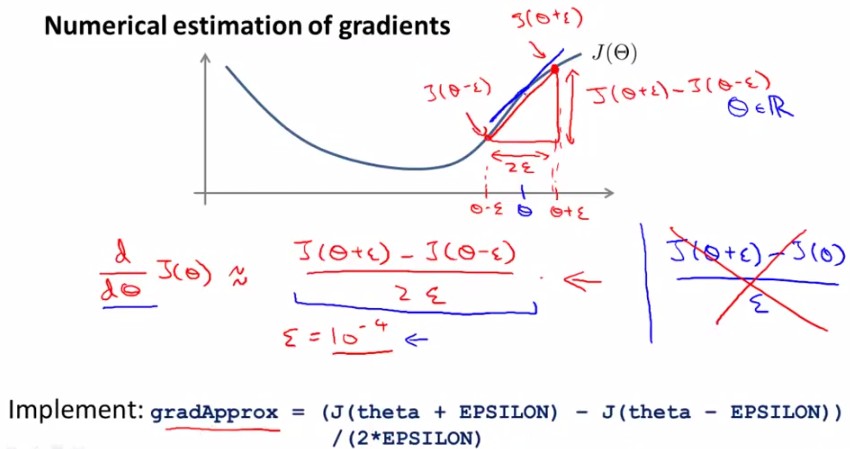

对于每个参数的求导公式如下图所示：

由于在back-propagation算法中我们一直能得到J(Θ)的导数D（derivative），那么就可以将这个近似值与D进行比较，如果这两个结果相近就说明code正确，否则错误，如下图所示：

Summary: 有以下几点需要注意

-在back propagation中计算出J(θ)对θ的导数D，并组成vector（Dvec）

-用numerical gradient check方法计算大概的梯度gradApprox=(J（Θ+ε）-J（Θ-ε）)/(2ε)

-看是否得到相同（or相近）的结果

-（这一点非常重要）停止check，只用back propagation 来进行神经网络学习（否则会非常慢，相当慢）

 

 

 

 

===============================

（六）、Random Initialization

对于参数θ的initialization问题，我们之前采用全部赋0的方法，比如：

this means all of your hidden units are computing all of the exact same function of the input. So this is a highly redundant representation. 因为一层内的所有计算都可以归结为1个，而这使得一些interesting的东西被ignore了。

所以我们应该打破这种symmetry，randomly选取每一个parameter，在[-ε,ε]范围内：

 

 

 

 

===============================

（七）、Putting it together

1. 选择神经网络结构

我们有很多choices of network :

那么怎么选择呢？

No. of input units: Dimension of features
No. output units: Number of classes
Reasonable default: 1 hidden layer, or if >1 hidden layer, have same no. of hidden units in every layer (usually the more the better)

2. 神经网络的训练

① Randomly initialize weights
② Implement forward propagation to get h_θ(x⁽ⁱ⁾) for anyx⁽ⁱ⁾
③ Implement code to compute cost function J(θ)
④ Implement backprop to compute partial derivatives

⑤

⑥

test:

 

本章讲述了神经网络学习的过程，重点在于back-propagation算法，gradient-checking方法，希望能够有人用我之前这篇文章中的类似方法予以实现神经网络。

另外提供一篇作为Reference，供大家参考。