NOJ 1641 错误的算法（模拟）

• [1641] 错误的算法

• 时间限制: 5000 ms　内存限制: 65535 K
• 问题描述

• 有道题目是这样的:

  输入一个 n 行 m 列网格,找一个格子,使得它所在的行和列中所有格子的数之和最大。如果答
  案不唯一,输出任意解即可。比如,在下面的例子中,最优解是(1,3),即第一行和的三列的交
  点(行从上到下编号为 1~n,列从左到右编号为 1~m),所有 7个数之和为 35。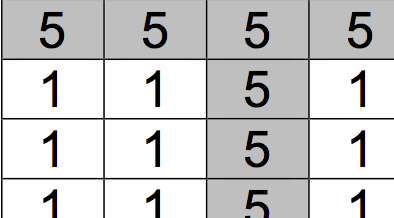

  

  快要比赛的时候,有一个裁判想到了这样一个算法: 

  首先找一行 r(1<=r<=n) 使得该行所有数之和最大,然后找一列 c(1<=c<=m) 使得该列 所有数之和最大,最后直接输出(r,c)。如果有多个满足条件的 r,输出最小的 r。对 于 c 同样处理。

  显然,这个算法是错的,但它竟然通过了大部分测试数据!你能找出那些让这个错误算法得到 正确结果的“弱”数据,以便裁判们改进这些数据吗?

• 输入
• 输入包含不超过 100 组数据。每组数据第一行为两个整数 n, m (1<=n<=500, 1<=m<=500),即行 数和列数。以下 n 行每行包含 m 个 1~100 的整数。输入的总大小不超过 2MB。
• 输出
• 对于每组数据,如果错误算法能得到正确结果,输出"Weak",否则输出"Strong"。
• 样例输入

• 4 4
  5 5 5 5
  1 1 5 1
  1 1 5 1
  1 1 5 1
  5 4
  2 5 1 1
  1 1 9 1
  1 1 1 1
  1 1 1 1
  1 1 1 1 

• 样例输出

• Case 1: Weak
  Case 2: Strong

昨晚做到十二点，经过聚聚的耐心教导（好吧我还是没听懂）后来去睡觉时又想了一会儿，知道了大神所说的不需要求正确解的意义（只要求正确解对应的SUM即可）。因为粗心忽略了题中的条件解可以为多个。因此只需证明题中裁判算法所给的解只是运气成分，碰巧正确而已。尼玛早上起来打开笔记本改了下代码果然AC了。我药丸啊

1、用题中所给条件算出裁判要的解。

2、用正确算法算出最优解们所符合的那个行列SUM值最大和MAX。

3、用裁判的解代入计算SUM的公式，要是错误，说明裁判的解错（Strong）。否则则是Weak。

代码：

#include<iostream>
#include<stdio.h>
using namespace std;
int list[510][510];
int hang,lie;
int sum1(int x,int y)
{
	int i,j,sum=0;
	for(i=x-1;i>=1;i--)
	{
		sum+=list[i][y];
	}
	for(i=x+1;i<=hang;i++)
	{
		sum+=list[i][y];
	}
	for(i=y-1;i>=1;i--)
	{
		sum+=list[x][i];
	}
	for(i=y+1;i<=lie;i++)
	{
		sum+=list[x][i];
	}
	return (sum+list[x][y]);
}
int main(void)
{
	int i,j,ar,ac,sum,inr,inc,max,co=0,tsum,rc;
	while(cin>>hang>>lie)
	{
		co++;
		for (i=1 ;i<=hang ;i++)
		{
			for (j=1; j<=lie; j++)
				cin>>list[i][j];
		}
		max=0;
		inr=1;
		for (i=1 ;i<=hang ;i++)
		{
			sum=0;
			for (j=1; j<=lie; j++)
			{
				sum+=list[i][j];
			}
			if(sum>max)
			{
				max=sum;
				inr=i;
			}
		}
		max=0;
		inc=1;
		for (j=1 ;j<=lie ;j++)
		{
			sum=0;
			for (i=1; i<=hang; i++)
			{
				sum+=list[i][j];
			}
			if(sum>max)
			{
				max=sum;
				inc=j;
			}
		}
		max=0;
		for(i=1;i<=hang;i++)
		{
			for(j=1;j<=lie;j++)
			{
				tsum=sum1(i,j);
				if(tsum>max)
				{
					max=tsum;
				}
			}
		}
		if(sum1(inr,inc)==max)
		{
			printf("Case %d: Weak\n",co);
		}
		else
		{
			printf("Case %d: Strong\n",co);
		}
		memset(list,0,sizeof(list));
	}
	return 0;
}