关于堆排序和topK算法的PHP实现

问题描述

topK算法，简而言之，就是求n个数据里的前m大个数据，一般而言，m<<n，也就是说，n可能有几千万，而m只是10或者20这样的两位数。

思路

最简单的思路，当然是使用要先对这n个数据进行排序，因为只有排序以后，才能按照顺序来找出排在前面的，或者排在后面的数据。

假如说我们用快拍，那么时间复杂度是O(nlogn)，但是仔细看题目，会发现实际上不要要将所有的数据就进行排序，因为我们找的是前m个数据，所以对所有数据排序实际上有些浪费了。所以可以想到，只维护一个大小为m的数组，然后扫一遍原来的数组n，只将大于数组m里的最小值的数据插入到m数组里，并且重新调整m数组的顺序。

如果使用朴素的方法对m数组进行调整，那么时间复杂度将会是O(n*m)，这显然不是最优的结果。对于维护的数组m，我们可以通过维护一个堆结构，来达到每次排序O（logm）的时间复杂度，这样topK算法，总体的复杂度也就变成了O(nlogm)。

关于堆

二叉堆是完全二叉树或者是近似完全二叉树。

二叉堆满足二个特性：

1．父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。

2．每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。

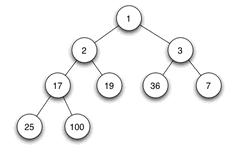
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆：一般都用数组来表示堆，i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。

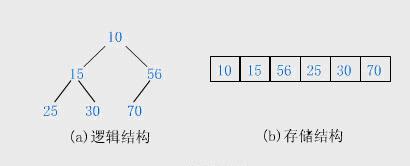
PHP实现的堆

 class Heap {

     protected $listSize;

     protected $tree;

     public function __construct($list) {

         $this->listSize = count($list);

         $i = 1;

         foreach ($list as $li) {

             $this->tree[$i++] = $li;

         }

         unset($list);

         $this->initHeap();

     }

     public function getSortedResult() {

         $this->initHeap();

         $this->sortHeap();

         return $this->tree;

     }

     public function getHeapResult() {

         return $this->tree;

     }

     public function getTopNode() {

         return $this->tree[1];

     }

     public function setTopNode($value) {

         $this->tree[1] = $value;

         $this->adjustHeap(1, $this->listSize);

     }

     public function sortHeap() {

         for ($end = $this->listSize; $end > 1; $end--) {

             $this->swap($this->tree[1], $this->tree[$end]);

             $this->adjustHeap(1, $end - 1);

         }

     }

     private function initHeap() {

         for ($start=floor($len / 2); $start >= 1; $start--) {

             $this->adjustHeap($start, $this->listSize);

         }

     }

     private function adjustHeap($start, $len) {

         $tmp = $start;  // 临时变量,用于保存最大值或者最小值的下标索引

         $lChildInx = $start * 2;

         $rChildInx = $lChildInx + 1;

         if ($start <= floor($len / 2)) {

             if($lChildInx <= $len && $this->tree[$lChildInx] < $this->tree[$tmp]) {

                 $tmp = $lChildInx;

             }

             if($rChildInx <= $len && $this->tree[$rChildInx] < $this->tree[$tmp]) {

                 $tmp = $rChildInx;

             }

             if ($tmp != $start) {

                 $this->swap($this->tree[$tmp], $this->tree[$start]);

                 $this->adjustHeap($tmp, $len);

             }

         }

     }

     private function swap(&$a, &$b) {

         $temp = $a;

         $a = $b;

         $b = $temp;

     }

 }

topK

 include 'Heap.class.php';   

 $list = range(1,10000);

 shuffle($list);

 $k = 15;

 $initHeapNodes = array_slice($list, 0, $k);

 $heap = new Heap($initHeapNodes);

 $n = count($list);

 for ($i=$k; $i<$n; $i++) {

     if ($list[$i] > $heap->getTopNode()) {

         $heap->setTopNode($list[$i]);

     }

 }

 print_r($heap->getSortedResult());