[NOIP2009] 提高组洛谷P1073 最优贸易

题目描述

C 国有 n 个大城市和 m 条道路，每条道路连接这 n 个城市中的某两个城市。任意两个

城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路，一部分

为双向通行的道路，双向通行的道路在统计条数时也计为 1 条。

C 国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价

格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息

之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 C 国 n 个城

市的标号从 1~ n，阿龙决定从 1 号城市出发，并最终在 n 号城市结束自己的旅行。在旅游的

过程中，任何城市可以重复经过多次，但不要求经过所有 n 个城市。阿龙通过这样的贸易方

式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品――水晶球，并在之后经过的另

一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 C 国旅游，他决定

这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

假设 C 国有 5 个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路

为单向通行，双向箭头表示这条道路为双向通行。

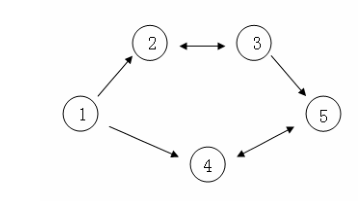
假设 1~n 号城市的水晶球价格分别为 4，3，5，6，1。

阿龙可以选择如下一条线路：1->2->3->5，并在 2 号城市以 3 的价格买入水晶球，在 3

号城市以 5 的价格卖出水晶球，赚取的旅费数为 2。

阿龙也可以选择如下一条线路 1->4->5->4->5，并在第 1 次到达 5 号城市时以 1 的价格

买入水晶球，在第 2 次到达 4 号城市时以 6 的价格卖出水晶球，赚取的旅费数为 5。

现在给出 n 个城市的水晶球价格，m 条道路的信息（每条道路所连接的两个城市的编号

以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

输入输出格式

输入格式：

第一行包含 2 个正整数 n 和 m，中间用一个空格隔开，分别表示城市的数目和道路的

数目。

第二行 n 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 n 个城

市的商品价格。

接下来 m 行，每行有 3 个正整数，x，y，z，每两个整数之间用一个空格隔开。如果 z=1，

表示这条道路是城市 x 到城市 y 之间的单向道路；如果 z=2，表示这条道路为城市 x 和城市

y 之间的双向道路。

输出格式：

输出文件 trade.out 共 1 行，包含 1 个整数，表示最多能赚取的旅费。如果没有进行贸易，

则输出 0。

输入输出样例

输入样例#1：

输出样例#1：

说明

【数据范围】

输入数据保证 1 号城市可以到达 n 号城市。

对于 10%的数据，1≤n≤6。

对于 30%的数据，1≤n≤100。

对于 50%的数据，不存在一条旅游路线，可以从一个城市出发，再回到这个城市。

对于 100%的数据，1≤n≤100000，1≤m≤500000，1≤x，y≤n，1≤z≤2，1≤各城市

水晶球价格≤100。

NOIP 2009 提高组第三题

正向BFS判联通，逆向BFS判路径上的最低价格。

 /*by SilverN*/

 #include<iostream>

 #include<algorithm>

 #include<cstring>

 #include<cstdio>

 #include<cmath>

 #include<vector>

 #include<queue>

 using namespace std;

 const int mxn=;

 int read(){

     int x=,f=;char ch=getchar();

     while(ch<'' || ch>''){if(ch=='-')f=-;ch=getchar();}

     while(ch>='' && ch<=''){x=x*+ch-'';ch=getchar();}

     return x*f;

 }

 vector<int>e1[mxn],ef[mxn];

 int w[mxn],mini[mxn];

 int n,m;

 bool arr[mxn];

 queue<int>q;

 void BFS(){

     q.push(n);

     arr[n]=;

     while(!q.empty()){

         int u=q.front();q.pop();

         for(int i=;i<ef[u].size();i++){

             int v=ef[u][i];

             if(!arr[v]){

                 arr[v]=;

                 q.push(v);

             }

         }

     }

     return;

 }

 bool inq[mxn];

 void SPFA(){

     q.push();

     inq[]=;

     while(!q.empty()){

         int u=q.front();q.pop();inq[u]=;

         for(int i=;i<e1[u].size();i++){

             int v=e1[u][i];

             int tmp=min(mini[v],min(mini[u],w[u]));

             if(mini[v]>tmp){

                 mini[v]=tmp;

                 if(!inq[v]){

                     inq[v]=;

                     q.push(v);

                 }

             }

         }

     }

     return;

 }

 int main(){

     int i,j;

     int x,y,z;

     n=read();m=read();

     memset(mini,0x3f,sizeof mini);

 //    for(i=1;i<=n;++i)w[i]=read(),mini[i]=w[i];

     for(i=;i<=n;++i)w[i]=read();

     for(i=;i<=m;++i){

         x=read();y=read();z=read();

         if(z==){

             e1[x].push_back(y);

             ef[y].push_back(x);

         }

         else{

             e1[x].push_back(y);

             e1[y].push_back(x);

             ef[x].push_back(y);

             ef[y].push_back(x);

         }

     }

     SPFA();

     while(!q.empty()) q.pop();

     BFS();

     int ans=;

     for(i=;i<=n;i++){

         if(arr[i])ans=max(ans,w[i]-mini[i]);

     }

     printf("%d\n",ans);

     return ;

 }