DNA比对算法：BWT

BWT算法，实质上是前缀树的一种实现。那么什么是前缀树呢？

一、前缀树

对于问题p in S？如果S=rpq，那么p为S前缀rp的一个后缀。

于是，为了判断p in S 是否成立，我们找到S的所有前缀，然后逐一判断p是不是它们的后缀。为了加快效率，我们将所有的前缀建成一颗树，这棵树便是前缀树。下面，我们举例说明前缀树的建立过程和如何使用前缀树进行模式匹配。

前缀树的建立

假设S='acaacg',p='aac',那么我们首先找到S的所有前缀，如下

a
ac
aca
acaa
acaac
acaacg

于是，我们将这些前缀翻转过来，然后建立为一颗字典树，如下图

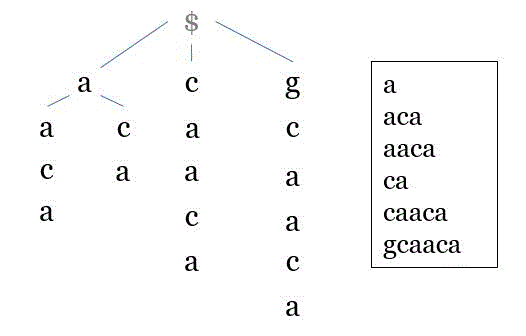
模式匹配

$p='aac'$，令$p'=caa$（即p的翻转）。显然，现在只需进行一次树的搜索，即可完成匹配。

如果在判断p in S 的同时，还需要得到p 在S 中的位置，那么只需在建树的时候，将每个字符的索引加上，例如

当然，也可以不保存索引，每次模式匹配结束时，沿着当前节点走下去，一直到为S[0]。

在节点中添加数字，有其他用处，详见我的另一篇博文广义后缀树的简介。

评价

我们可以看到，相对于常规的匹配算法，前缀树时间复杂度比较小，但占用空间较大。下面要说的BWT算法，就是解决这个问题的。

二、构建BWT(S)

仍然，以S='acaacg'为例。

令S1=S+'\$'='acaacg\$'；

循环左移S1 6次，得到S2,S3,S4,S5,S6,S7；

'acaacg\$'

'caacg\$a'

'aacg\$ac'

'acg\$aca'

'cg\$acaa'

'g\$acaac'

'\$acaacg'

对S1到S7按字典序排序（\$字符的字典序最小），取每个串的最后一个字符，连成一个序列'gc\$aaac'。于是为BWT(S)='gc\$aaac'。

'\$acaacg'

'aacg\$ac'

'acaacg\$'

'acg\$aca'

'caacg\$a'

'cg\$acaa'

'g\$acaac'

也许，到这里，你还不清楚BWT变换和前缀树，有什么关系。那就接着往下看吧。

三、使用BWT,进行模式匹配

我们已经知道BWT(S)='gc\$aaac'，对BWT(S)中的字符进行排序得到S'='\$aaaccg'，得到下图形式的矩阵。

这个矩阵看起来，有些规律，但是又很奇怪。下面通过复原S的过程，我们来理解以下这个矩阵。

复原S

这个过程用语言描述比较麻烦，直接看图

按照图中(1)到(7)步，我们即可得到'$gcaaca'，于是S='acaacg'。

其中，斜线表示是，我们找到最后一列的某个符号，然后跳至这个符号在第一列的位置。比如，在第(2)步中，最后一列为第2个c，我们跳到第一行中第2个c的位置。

模式匹配

p='aac'，令$p'='caa'$，选取c作为起点，由于S中有两个c，因此有两种可能的匹配。

从第一个c出发
从第二个c出发

因此，在方案2得到p',因此p in S是正确的。

几个问题

问题一：如何得到某个符号，在本列中是第几个？

显然，我们可以使用一个数组来保存。例如，对于'$gcaaca'，数组a=[1,1,1,1,2,2,3]。
$ g c a a c a
[1,1,1,1,2,2,3]

但是，还有一种省空间的办法。我们只保存串'$gcaaca'中某些字符的位置，这些字符我们称为checkpoint。

问题二：如何得到模式p在S中的位置？

匹配模式串之后，继续运行，直至\$，但是这样比较耗时。

另一种办法，在BWT串中记录相应的偏移。这种办法空间开销比较大，也可以采取类似于checkpoint的方法，记录部分的偏移。

四、待研究的问题

如何快速得到一个串的BWT编码?
如何允许部分匹配？

题外话

DNA比对还有一类快速的办法——使用哈希。