R语言结合概率统计的体系分析---数字特征

现在有一个人，如何对这个人怎么识别这个人？那么就对其存在的特征进行提取，比如，提取其身高，其相貌，其年龄，分析这些特征，从而确定了，这个人就是这个人，我们绝不会认错。

同理，对数据进行分析，也是提取出数据的特征，对其特征进行分析，从而确定这些数据所呈现的信息状况，从而确定了这些数据的独特性和唯一性，因为他呈现的信息是唯一的，绝不与别的是相同的。

那么这些特征是什么呢？拥有哪些特征呢？似乎应该是经过无数科学家的总结，终于发现了几个重要的特征，包括数字特征和分布特征，这个数字特征，包括集中位置，分散程度，而后整体分布，就是一个总体的描述，其实，这里就有一个疑惑，数字特征和分布特征，到底有什么区别？他们依靠什么来从本质上加以区分开来的呢？

可以试着从一个角度来分析一下，数字特征，也就是说集中位置和分散程度是一个数，在坐标上，他仅仅代表着一个点，一个数字而已。而分布特征，则表现为一个图形，他可以是二维的图形，也可以是三维的图形，甚至可以是N维的图形。所以可以说，数字特征和分布特征，分别是数据信息在低维度和高纬度上面体现。

最后，我们为什么要分析数据？分析数据有何种意义可言？其实，就像我们认识分析一个人的特征是为了判断一个人一样，我们分析数据的特征，就是为了统计推断，为其服务的。

明白了以上的要点，初步建立了一个良好的逻辑结构和逻辑起点，即为数据---》特征分析---》信息呈现---》统计推断，下面就可以把所有的目光聚集在其中一个关键而又核心的位置了，即为特征分析。

问题在于，现在已经要研究集中位置，分散程度和整体分布，那么用什么东西描述他，或者说，用什么东西来表现他？

先来说，集中位置。

常用来表现集中位置的，有均值，众数，中位数和百分位数

1，均值：

简单，就是平均数咯。

公式的定义为：

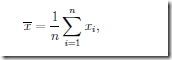
在R语言中，求均值的公式为mean(x),x为样本，可以为向量，在这里不得不提一下，向量，在线性代数中有一个解释，即为向量就是一组有序的数组，这个定义放在这里是最恰当不过了。从数据分析的角度来说，只有一个数据，不存在分析的必要性，如果数据多了，就有了分析的必要，这些多的数据，放在一起，从而组成一组数。这组数在数学上的表示，就成了向量。

那么为什么向量可以表示有序数组，可以其实这么想，我现在把向量的起始点规定在坐标的原点，那么向量的终点就可以非常固定而又准确的表示出一个点了，这个点，在不同维度之中，表示这个点的数字也或多或少，比如在一位坐标中，也就是数轴上，这个点就只有一个数，令为a。在二维空间中，这个点为(a,b)，在三维空间中，这个点为(a,b,c)，四维空间中，这个点的坐标为（a,b,c,d）,同理，在n维空间之中，这个点的坐标为（a,b,c,d........），看着这样的规律，可见，向量可以正好表示存在的一组数，不论这组数中到底存在着多少的数据，这也是为什么线性代数中为什么要这么定义向量的原因了。

如果你只看大学课本里的那本线性代数，你会发现那里只是突然给出了向量的新的定义，至于为什么给出新的定义，他就没有说了，我想说的是，这还是教科书么？也许仅仅就是一个工具书而已，由此可见，中国的教育在高等层次上，还是做的很烂的，我都不禁怀疑，那些家伙到底也理解透了么？这或许是中国数学为什么在后期阶段都乏力的原因吧，能够给予我们良好指导的老师，几乎缺乏。。

其实吧，我觉得，线性代数，那一本书，本质上讲的就是有序数组，有序数组和有序数组之前的关系的学问，如果他本质上讲的向量，或者本质上讲的是矩阵，那么到底谁是本质，到底，谁才是本质上真正由起始的表现谁？所以说，他们最终都只是有序数组的一体两面而已。。。

不多说了，回到正题。。。

   是把求平均值运用到矩阵当中，1，表示的行求平均，如果变为2，则表示，列求平均。

2，众数

也就是出现最多的数

3，中位数

就是处在一组数中间的数据，在获取这个中间数之前，必须先对这组数进行排序

排序的函数为：sort( )

中位数的公式：

对应的函数：

4，百分位数

所谓百分位数，比如样本总数为20，把他分为100个等分，即为20/100，如果在其25百分位数，即为20*25/100=20*25%=20/4=5,则这时，我们研究的数字就指向的第五个数。

R语言中的函数：

在来说说分散程度。。

这里只说说两种表现的方法，极差和方差。

所谓极差就是最大值和最小值的差距，常人的一般判断，都晓得最大值和最小值的差很容易就知道，这个的确是可以表示一组数据的分散程度的。

然而如下：

2，7,8,10    2,5,6,10

这两种数据，很显然就不能够用极差来判别他的分散程度了，就必须得另外想办法。

可以使用|2-10+7-8|    |2-10+5-6|   容易得出后者的分散程度较小，然而这种计算方法显得有点不方便，他需要把数据分为几个部分来计算，增加了计算的复杂程度，那么有不有更加简单，效果却一样的方法呢？

　　可以观察有，5-6 其实是等于，5-5.5+5.5-6  中间其实有平均数在作用。

所以我们用每个数，减去其平均数，由于有正有负，又由于绝对值不方便计算，所以加上一个平方，从而得到一个平方差之和来表达一组数的离散，但仅仅是平方和相加么？那么几组数中数据的多少不同呢？这样就不好比较了，所以，再对这一平方和取得一个平均数，这样就可以比较了，这样，我们就得到了方差，公式为：

最后，在这一篇，说说前面几个表示集中位置的方法的区别，当存在离群非常明显的数据的时候，均值，就不能够很好的显示一组数据的集中位置，这个时候，就得靠众数和中位数，至于百分位数，可以用来显示特征的特征，即任意其中一个数，正整体中所表现的状态，如，小明的50分的成绩，在全班成绩中所在的位置，如果他的成绩，即50分处在75百分数，则表示他的成绩是是在中上游的。

下一篇，将讲分布和绘图体系。