bzoj 3626: [LNOI2014]LCA

Description

给出一个n个节点的有根树（编号为0到n-1，根节点为0）。一个点的深度定义为这个节点到根的距离+1。
设dep[i]表示点i的深度，LCA(i,j)表示i与j的最近公共祖先。
有q次询问，每次询问给出l r z，求sigma_{l<=i<=r}dep[LCA(i,z)]。
（即，求在[l,r]区间内的每个节点i与z的最近公共祖先的深度之和）

Input

第一行2个整数n q。
接下来n-1行，分别表示点1到点n-1的父节点编号。
接下来q行，每行3个整数l r z。

Output

输出q行，每行表示一个询问的答案。每个答案对201314取模输出

Sample Input

5 2
0
0
1
1
1 4 3
1 4 2

Sample Output

8
5

HINT

共5组数据，n与q的规模分别为10000,20000,30000,40000,50000。

Source

数据已加强 by saffah

Orz这题真的太鬼了，除了暴力求LCA再暴力求根本想不到该怎么做，小伙子啊，迟早要完！！！

看了题解之后膝盖又一次跪烂了。。。

于是接下来就一步一步还原大佬们是怎么YY出来的吧

新暴力雏形：

对于每个z,我们把z到根节点上的所有点都打上标记，然后对于区间[l,r]的点就不断向上跳爸爸，直到跳到一个打了标记的点，把这个点的深度加上。。。

也就是说只有这些被z跳到的点的深度才是有贡献的。。。

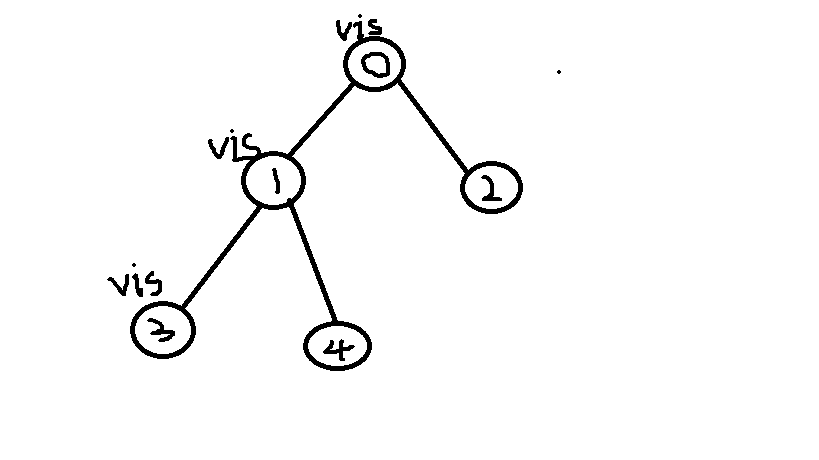
考虑到深度的定义。。。

于是有了并没有一点改进的暴力：

把z到根的路径上的点权加1，l--r中的每个点的贡献相当于查询该点到根节点的路径上的权值和(这个值也就等价于第一种暴力中找到的第一个有标记的点的深度。。。)

这样手动模拟或脑子YY是显然没有问题的。。。

我们发现这种操作是有可逆性的，重复性的(深度叠加)。。。

那么上面的第二种暴力的做法等价于如下做法：

把l--r间的每个点到根节点路径上的点权加1，然后对于每个z，其答案就是z到根的权值和。。。

于是就变成了下面这样：

于是我们可以想到一个比较明显的做法了。。。依次加入0--n-1的点并把该点到根的路径上的点权加1；

我们考虑用前缀和的思想，即用ans[r]-ans[l-1]。。。

我们对于每个询问的l和r拆成两个询问，把这些询问离线下来sort一遍，维护一个head指针一直加点。。。，head指针是单增的，

就不需要像CJK神犇那样对每个询问l和r还要打个莫队。。。

我们需要一个数据结构来维护区间修改和区间求和。。。于是我做死的打了一个LCT，相当于只要下放lazy和维护一个子树大小。。。

附上代码：

 // MADE BY QT666
 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 #include<iostream>
 #include<queue>
 #include<set>
 #include<cstdlib>
 #include<cstring>
 #include<string>
 #include<ctime>
 #define lson num<<1
 #define rson num<<1|1
 #define int long long
 using namespace std;
 typedef long long ll;
 const int N=;
 const int mod=;
 int gi()
 {
   int x=,flag=;
   char ch=getchar();
   while(ch<''||ch>''){if(ch=='-') flag=-;ch=getchar();}
   while(ch>=''&&ch<='') x=x*+ch-'',ch=getchar();
   return x*flag;
 }
 int c[N][],fa[N],st[N],sum[N],rev[N],lazy[N],size[N],v[N],f[N];
 int ans[N][];
 int n,m;
 struct ac
 {
     int l,id,z,type;
 }q[N];
 inline bool cmp(const ac &a,const ac &b) {return a.l<b.l;}
 inline bool isroot(int x) {return c[fa[x]][]!=x&&c[fa[x]][]!=x;}
 inline void update(int x)
 {
     int l=c[x][],r=c[x][];
     sum[x]=sum[l]+sum[r]+v[x];
     size[x]=size[l]+size[r]+;
 }
 inline void solvelazy(int x,int y)
 {
     v[x]+=y;
     lazy[x]+=y;
     sum[x]+=y*size[x];
 }
 inline void pushdown(int x)
 {
     int l=c[x][],r=c[x][];
     if(rev[x])
         {
             rev[x]^=;rev[l]^=;rev[r]^=;
             swap(c[x][],c[x][]);
         }
     if(lazy[x])
         {
             if(c[x][]) solvelazy(c[x][],lazy[x]);
             if(c[x][]) solvelazy(c[x][],lazy[x]);
             lazy[x]=;
         }
 }
 inline void rotate(int x)
 {
     int y=fa[x],z=fa[y],l,r;
     if(c[y][]==x)l=;else l=;r=l^;
     if(!isroot(y))
         {
             if(c[z][]==y) c[z][]=x;
             else c[z][]=x;
         }
     fa[y]=x;fa[x]=z;fa[c[x][r]]=y;
     c[y][l]=c[x][r],c[x][r]=y;
     update(y),update(x);
 }
 inline void splay(int x)
 {
     int top=;st[++top]=x;
     for(int i=x;!isroot(i);i=fa[i]) st[++top]=fa[i];
     for(int i=top;i;i--) pushdown(st[i]);
     while(!isroot(x))
         {
             int y=fa[x],z=fa[y];
             if(!isroot(y))
                 {
                     if(c[y][]==x^c[z][]==y) rotate(x);
                     else rotate(y);
                 }
             rotate(x);
         }
 }
 inline void access(int x)
 {
     int t=;
     while(x)
         {
             splay(x);
             c[x][]=t;
             t=x;update(x);x=fa[x];
         }
 }
 inline void rever(int x) {access(x);splay(x);rev[x]^=;}
 inline void lnk(int x,int y) {rever(x);fa[x]=y;}
 inline int query(int x,int y) {rever(x);access(y);splay(y);return sum[y];}
 inline void add(int x,int y) {rever(x);access(y);splay(y);lazy[y]++;v[y]++;sum[y]+=size[y];}
 main()
 {
     n=gi();m=gi();
     int l,r,tot=,z;
     for(int i=;i<=n;i++) f[i]=gi(),f[i]++,lnk(i,f[i]);
     for(int i=;i<=m;i++)
         {
             l=gi(),r=gi(),z=gi();
             l++;r++;z++;
             q[++tot].l=l-,q[tot].id=i,q[tot].z=z;q[tot].type=;
             q[++tot].l=r,q[tot].id=i,q[tot].z=z;q[tot].type=;
         }
     sort(q+,q++tot,cmp);
     int head=;
     for(int i=;i<=tot;i++)
       {
           while(head<=q[i].l) add(,head),head++;
           ans[q[i].id][q[i].type]=query(,q[i].z);
       }
     for(int i=;i<=m;i++) printf("%lld\n",(ans[i][]-ans[i][])%mod);
     return ;
 }