洛谷 P1330 封锁阳光大学题解

题目描述

曹是一只爱刷街的老曹，暑假期间，他每天都欢快地在阳光大学的校园里刷街。河蟹看到欢快的曹，感到不爽。河蟹决定封锁阳光大学，不让曹刷街。

阳光大学的校园是一张由N个点构成的无向图，N个点之间由M条道路连接。每只河蟹可以对一个点进行封锁，当某个点被封锁后，与这个点相连的道路就被封锁了，曹就无法在与这些道路上刷街了。非常悲剧的一点是，河蟹是一种不和谐的生物，当两只河蟹封锁了相邻的两个点时，他们会发生冲突。

询问：最少需要多少只河蟹，可以封锁所有道路并且不发生冲突。

输入格式

第一行：两个整数N，M

接下来M行：每行两个整数A，B，表示点A到点B之间有道路相连。

输出格式

仅一行：如果河蟹无法封锁所有道路，则输出“Impossible”，否则输出一个整数，表示最少需要多少只河蟹。

输入输出样例

输入 #1复制

3 3
1 2
1 3
2 3

输出 #1复制

Impossible

输入 #2复制

3 2
1 2
2 3

输出 #2复制

1

说明/提示

【数据规模】

1<=N<=10000，1<=M<=100000，任意两点之间最多有一条道路。

---

题解

本题实际上是一道二分图的题目。

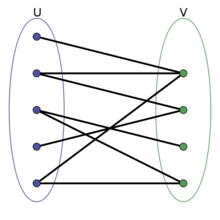
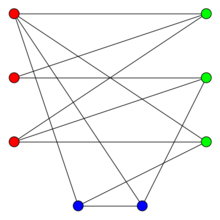
如果我们把图中U、V两个集合中的所有连线都用河蟹断开，就达到了题目要求。要判断图中的二分图，只需要类似01迷宫进行BFS遍历染色即可。在染色的过程中，如果发现连线的另一个端点未染色，就用和当前端点不同的颜色染色，要是已经染色且和当前节点颜色相同，就说明构成循环圈，不能构成二分图，类似下图的情况。

代码如下：

 #include <iostream>
 #include <math.h>
 #include <stdio.h>
 #include <algorithm>
 #include <string.h>

 using namespace std;

 const int MAXN = ;
 int first[MAXN], n, m, en, color[MAXN], f[], u, v; //f统计不同颜色节点数
 int front, rear;
 bool vis[MAXN];
 int ans;

 struct edge
 {
     int zhongdian, changdu;
     int next;
 };

 edge ed[MAXN]; 

 void add_edge(int s, int e, int d)
 {
     en++;
     ed[en].next = first[s];
     first[s] = en;
     ed[en].zhongdian = e;
     ed[en].changdu = d;
 }

 struct Node
 {
     int x, y;
     int step;
 };
 Node q[MAXN];

 int bfs(int a)
 {
     Node now, next;
     now.x = a;
     vis[a] = ;
     color[a] = ;
     f[] = ;
     f[] = ;
     front = rear = ;
     q[rear] = now;
     rear++;
     while(front < rear)
     {
         now = q[front++];
         for(int i = first[now.x]; i; i = ed[i].next)
         //first[now]：当前点的第一条边；ed[i].next：下一个访问的点
         {
             if(color[ed[i].zhongdian] != -)
             {
                 if(color[ed[i].zhongdian] == color[now.x])
                 {
                     cout << "Impossible" << endl;
                     return -;
                 }
             }
             else
             {
                 color[ed[i].zhongdian] = (color[now.x] + ) % ;
                 q[rear].x = ed[i].zhongdian;
                 rear++;
                 f[color[ed[i].zhongdian]]++;
             }
         }
     }
     ans += min(f[], f[]);
 }

 int main()
 {
     cin >> n >> m;
     for(int i = ; i <= n; i++)
     {
         color[i] = -; //初始化
     }
     for(int i = ; i <= m; i++)
     {
         cin >> u >> v;
         add_edge(u, v, );
         add_edge(v, u, );
     }
     for(int i = ; i <= n; i++)
     {
         if(color[i] == -)
         {
             if(bfs(i) < )
             {
                 return ;
             }
         }
     }
     cout << ans << endl;

     return ;
 }

代码中的f数组是用来统计黑白两种染色点的个数的，本题所求的最小河蟹数就是两种染色点个数的最小值。