SPFA + 链式前向星(详解)

求最短路是图论中最基础的算法，最短路算法挺多，本文介绍SPFA算法。关于其他最短路算法，请看我另一篇博客最短路算法详解

链式前向星概念

简单的说，就是存储图的一个数据结构。它是按照边来存图，而邻接矩阵是按点来存图，故链式前向星又叫边集数组

为何用链式前向星

当图的边数不多，而节点数很多(稠密图)的时候，如果我们仍然用邻接矩阵来存的话，内存占用可能会很大，而这种情况在ACM竞赛中又是很常见的，此时链式前向星就显得尤为重要。

链式前向星详解

主要涉及到两个数组，一个是head[MAXE]数组，另一个是edge[MAXE]数组：

// edge数组是一个边集数组，存放一条边的信息

// to --- 该条边的终点

// next --- 下一条要访问的边(存的是edge数组的下标).

// 即：访问完了edge[i]，下一条要访问的就是edge[edge[i].next]，

// 如果next为0，表示now这个节点作为起点的边已经全部访问完.(下一步:Q.front())

// w --- 该条边的权值

struct Node {

int to,next,w;

};

Node edge[MAXE];

// idx --- edge数组的下标

// head[i] --- 表示以i节点为起点的所有出边在edge数组中的起始存储位置为head[i].

// (如果head[i]为0，表示结点i没有出边)

int idx,head[MAXV];

理解了这两个数组，那么链式前向星也就理解了。其实链式前向星主要还是理解head数组和edge数组中的next这两个东西是怎么相互作用的，简单的说，就是head数组指导next，next指导edge的下一个下标。即：head[i]存储的是节点i作为起始节点的出边在edge数组中的起始存储位置，next引导节点i的下一条出边在edge数组中的存储位置。

怎么实现图的存储的呢？

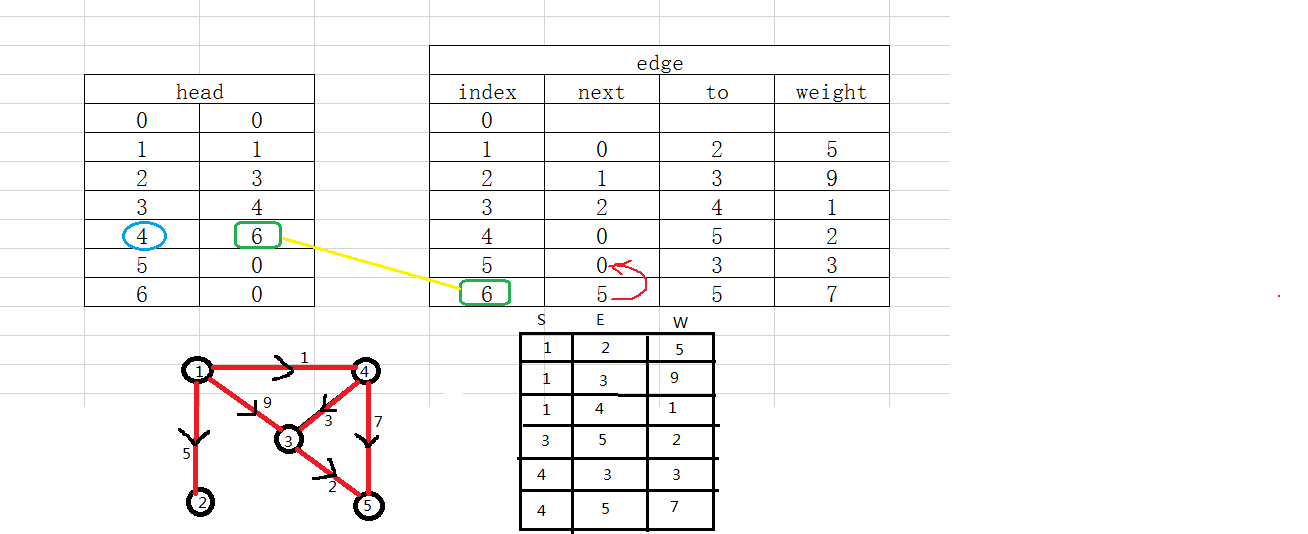
这张图看懂了，链式前向星也就搞懂了。

链式前向星代码实现

//Memory   Time

// 2556K    362MS

// by : Snarl_jsb

#include<algorithm>

#include<cstdio>

#include<cstring>

#include<cstdlib>

#include<iostream>

#include<vector>

#include<queue>

#include<stack>

#include<iomanip>

#include<string>

#include<climits>

#include<cmath>

#define MAXV 10010

#define MAXE 50010

#define LL long long

using namespace std;

int T,n,m,u,v,w;

int now,home,goal;

bool vis[MAXV];

LL dis[MAXV];

namespace Adj

{

        // edge数组是一个边集数组，存放一条边的信息

        // to --- 该条边的终点

        // next --- 下一条要访问的边(存的是edge数组的下标).

        // 即：访问完了edge[i]，下一条要访问的就是edge[edge[i].next]，

        // 如果next为0，表示now这个节点作为起点的边已经全部访问完.(下一步:Q.front())

        // w --- 该条边的权值

        struct Node

        {

                int to,next,w;

        };

        Node edge[MAXE];

        // idx --- edge数组的下标

        // head[i] --- 表示以i节点为起点的所有出边在edge数组中的起始存储位置为head[i].(如果head[i]为0，表示结点i没有出边)

        int idx,head[MAXV];

        // 初始化

        void init()

        {

                idx=;

                memset(head,,sizeof(head));

        }

        // 加边函数

        void addEdge(int u,int v,int w) // 起点，终点，权值

        {

                edge[idx].to=v;   // 该边的终点

                edge[idx].w=w;    // 权值

                edge[idx].next=head[u]; //  (指向head[u]后，head[u]又指向了自己)

                head[u]=idx;  // 以u结点为起点的边在edge数组中存储的下标

                idx++;

        }

}

using namespace Adj;

void visit(int sta)

{

    for(int i=;i<=n;i++)

    {

        vis[i]=;

        dis[i]=LLONG_MAX;

    }

    // 起点进队

    queue<int>Q;

    Q.push(sta);

    vis[sta]=;

    dis[sta]=;

    while(!Q.empty())

    {

        int now=Q.front();

        Q.pop();

        // 在spfa中这儿需要改为0，因为每个节点需要重复进队

        vis[now]=;

        //取出now结点在edge中的起始存储下标(当i=0，即edge[i].next为0，说明以now节点为起始点的边全部访问完)

        for(int i=head[now];i;i=edge[i].next)

        {

            int son=edge[i].to;

            printf("%d --> %d  , weight = %d\n",now,edge[i].to,edge[i].w);

            if(!vis[son])

            {

                Q.push(son); // 子节点未访问过

                vis[son]=; //  标记已访问

            }

        }

    }

}

int main()

{

    while()

    {

       Adj::init();

       scanf("%d",&n);

       scanf("%d",&m);

       while(m--) // 输入m条边

       {

               int s,e,w; // 起点 终点 权值

               scanf("%d %d %d",&s,&e,&w);

               addEdge(s,e,w);  //若是无向图，反过来再加一次

       }

       int start_point;   //访问的起点

       scanf("%d",&start_point);

       visit(start_point);

    }

    return ;

}

spfa概念

SPFA算法是求单源最短路径的一种算法，在Bellman-ford算法的基础上加上一个队列优化，减少了冗余的松弛操作，是一种高效的最短路算法。

SPFA的运用和分析
运用：

求单源最短路；
判断负环(某个点进队的次数超过了v次，则存在负环)

分析：

平均时间复杂度：O(kE),k<=2
最差时间复杂度：O(VE) (出题人可能设计卡spfa时间复杂度的数据)

SPFA代码实现

//Memory   Time

// 2556K    362MS

// by : Snarl_jsb

#include<algorithm>

#include<cstdio>

#inlude<cstring>

#include<cstdlib>

#include<iostream>

#include<vector>

#include<queue>

#include<stack>

#include<iomanip>

#include<string>

#include<climits>

#include<cmath>

#define MAXV 10010

#define MAXE 50010

#define LL long long

using namespace std;

int T,n,m,u,v,w;

int now,home,goal;

bool vis[MAXV];

LL dis[MAXV];

namespace Adj

{

        // edge数组是一个边集数组，存放一条边的信息

        // to --- 该条边的终点

        // next --- 下一条要访问的边(存的是edge数组的下标).即：访问完了edge[i]，下一条要访问的就是edge[edge[i].next]，如果next为0，表示now这个节点作为起点的边已经全部访问完.(下一步:Q.front())

        // w --- 该条边的权值

        struct Node

        {

                int to,next,w;

        };

        Node edge[MAXE];

        // idx --- edge数组的下标

        // head[i] --- 表示以i节点为起点的所有出边在edge数组中的起始存储位置为head[i].(如果head[i]为0，表示结点i没有出边)

        int idx,head[MAXV];

        // 初始化

        void init()

        {

                idx=;

                memset(head,,sizeof(head));

        }

        // 加边函数

        void addEdge(int u,int v,int w) // 起点，终点，权值

        {

                edge[idx].to=v;   // 该边的终点

                edge[idx].w=w;    // 权值

                edge[idx].next=head[u]; //  (指向head[u]后，head[u]又指向了自己)

                head[u]=idx;  // 以u结点为起点的边在edge数组中存储的下标

                idx++;

        }

}

using namespace Adj;

void visit(int sta)

{

    for(int i=;i<=n;i++)

    {

        vis[i]=;

        dis[i]=LLONG_MAX;

    }

    // 起点进队

    queue<int>Q;

    Q.push(sta);

    vis[sta]=;

    dis[sta]=;

    while(!Q.empty())

    {

        int now=Q.front();

        Q.pop();

        vis[now]=;  // 在spfa中这儿需要改为0，因为每个节点需要重复进队

        for(int i=head[now];i;i=edge[i].next)  //取出now结点在edge中的起始存储下标(当i=0，即edge[i].next为0，说明以now节点为起始点的边全部访问完)

        {

            int w=edge[i].w;

            int son=edge[i].to;

            printf("%d --> %d  , weight = %d\n",now,edge[i].to,edge[i].w);

            if(dis[now]+w<dis[son]) // 松弛操作

            {

                    dis[son]=dis[now]+w;

                    if(!vis[son])

                    {

                        Q.push(son); // 子节点未访问过

                        vis[son]=; //  标记已访问

                    }

            }

        }

    }

    puts("/*************************************** END ******************************************/");

    for(int i=;i<=n;++i)

    {

            printf("%d --> %d shortest distance is %d\n",sta,i,dis[i]);

    }

}

int main()

{

    while()

    {

       Adj::init();

       scanf("%d",&n);

       scanf("%d",&m);

       for(int i=;i<=m;++i) // 输入m条边

       {

               int s,e,w; // 起点 终点 权值

               scanf("%d %d %d",&s,&e,&w);

               addEdge(s,e,w);  //若是无向图，反过来再加一次

       }

       int start_point;   //访问的起点

       scanf("%d",&start_point);

       visit(start_point);

    }

    return ;

}

/*

5 6

1 2 5

1 3 9

1 4 1

3 5 2

4 3 3

4 5 7

1

*/