manim边做边学--隐函数图像

在数学可视化中，显函数$ y=f(x) \(相对容易处理，但**隐函数**\) F(x,y)=0 $的绘制则更具挑战性。

Manim库中的ImplicitFunction类专门用于解决这个问题，它能够高效地绘制各种复杂的隐函数曲线。

ImplicitFunction的典型应用场景包括：

• 高等数学教学：绘制圆锥曲线（椭圆、双曲线）、心形线、双纽线等
• 工程应用：可视化等值线、等高线、势能面
• 物理模拟：绘制电场/磁场的等势线、相平面轨迹
• 计算机图形学：生成特殊曲线和曲面
• 代数几何：研究代数曲线的性质

今天，我们将深入探讨Manim中的ImplicitFunction类，了解其作用、应用场景以及如何通过实际示例展示其强大功能。

1. 主要参数

ImplicitFunction的主要参数有：

参数	类型	说明
func	Callable[[float, float], float]	必需参数，二元函数F(x,y)
x_range	Sequence[float]	x轴的取值范围，如[-3,3]
y_range	Sequence[float]	y轴的取值范围，如[-3,3]
color	Color	曲线颜色，默认为WHITE
min_distance	float	点之间的最小距离（控制曲线精度）
max_quads	int	用于渲染的最大四边形数量（性能优化）
use_smoothing	bool	是否使用平滑处理（默认True）
delta	float	采样步长（影响曲线精度）

func参数是隐式函数的形式，这个函数需要接受两个浮点数$ x \(和\) y $，并返回一个浮点数。

2. 主要方法

ImplicitFunction的主要方法有：

名称	说明
generate_points	初始化points属性，从而定义形状。这个方法在对象创建时被调用
init_points	与generate_points类似，用于初始化points属性

3. 使用示例

为了更好地理解ImplicitFunction的功能，我们将通过几个示例来展示其在不同场景中的应用。

3.1. 基本隐函数（圆）

这个示例展示最基本的隐函数绘制，通过方程$ x^2+ y^2 = 1 $绘制单位圆。

注意x_range和y_range的设置需要包含整个曲线。

# 创建隐函数图像（单位圆）
circle = ImplicitFunction(
    lambda x, y: x**2 + y**2 - 1,
    color=RED,
    x_range=[-1.5, 1.5],
    y_range=[-1.5, 1.5],
)

# 添加标签
label = MathTex("x^2 + y^2 = 1").next_to(circle, DOWN)

# 动画展示
self.play(Create(circle), Write(label))

3.2. 动态参数变化（椭圆）

这个示例使用ValueTracker和always_redraw实现动态变化的椭圆，展示如何通过改变参数实时更新隐函数图像。

# 创建参数跟踪器
a = ValueTracker(1)
b = ValueTracker(1)

# 创建动态椭圆
ellipse = always_redraw(
    lambda: ImplicitFunction(
        lambda x, y: (x**2) / (a.get_value() ** 2)
        + (y**2) / (b.get_value() ** 2)
        - 1,
        color=GREEN,
        x_range=[-4, 4],
        y_range=[-3, 3],
    )
)

# 添加参数标签
param_label = always_redraw(
    lambda: MathTex(
        f"\\frac{{x^2}}{{{a.get_value()**2:.1f}}} + \\frac{{y^2}}{{{b.get_value()**2:.1f}}} = 1",
        color=RED,
    )
    .shift(DOWN * 1.5 + RIGHT * 1.8)
    .scale(0.6)
)

self.add(ellipse, param_label)
self.play(a.animate.set_value(2), b.animate.set_value(1.5), run_time=3)
self.play(a.animate.set_value(3), b.animate.set_value(1), run_time=3)

3.3. 复杂曲线（笛卡尔心形线）

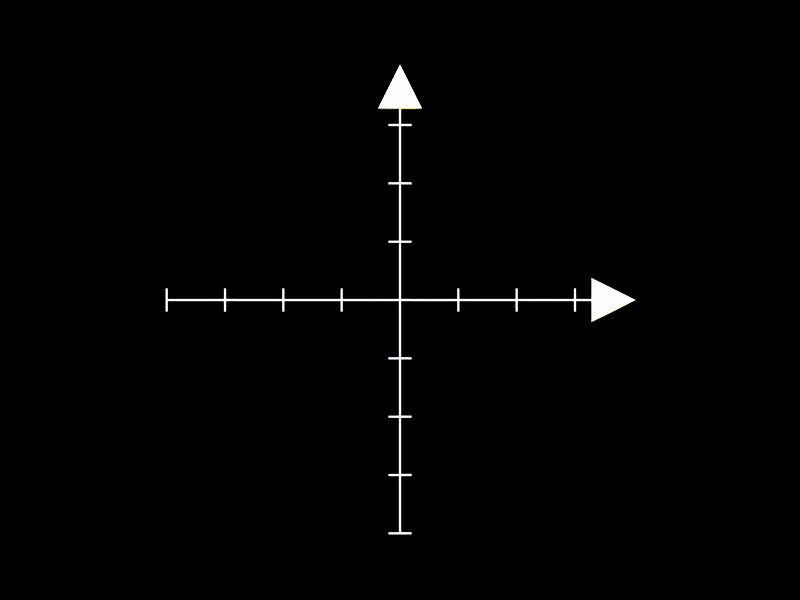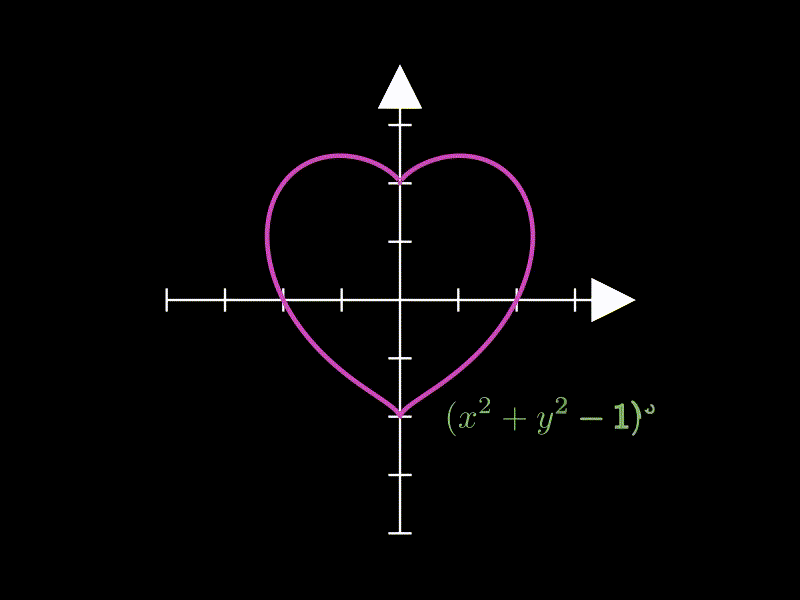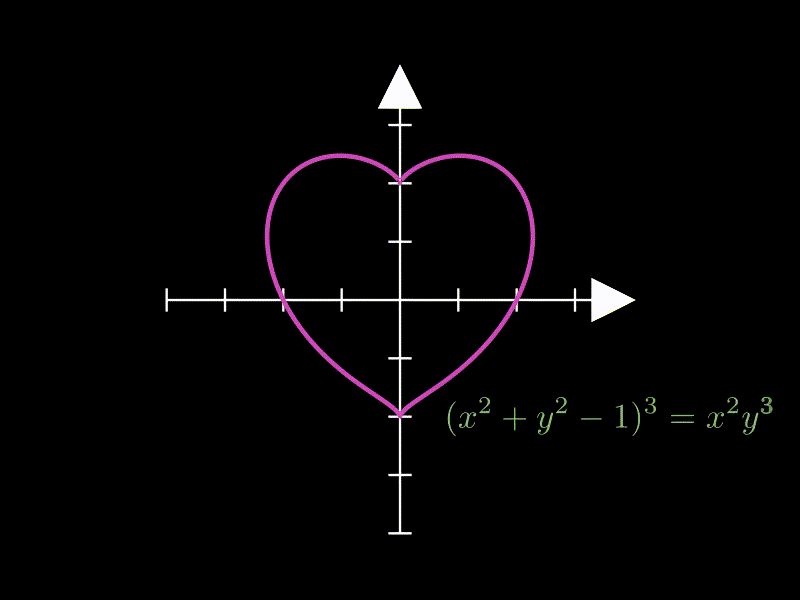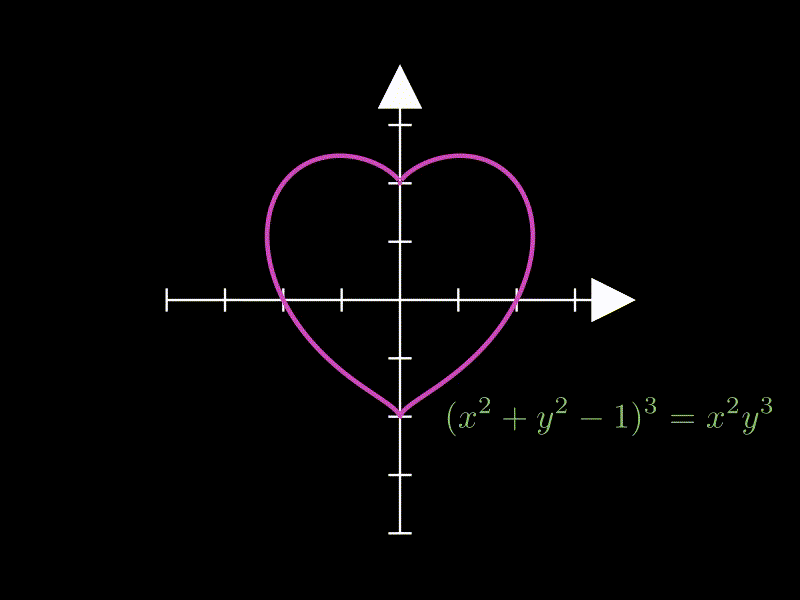
这个示例展示复杂隐函数的绘制，绘制了一个心形曲线。

        # 创建心形线
        heart = ImplicitFunction(
            lambda x, y: (x**2 + y**2 - 1) ** 3 - x**2 * y**3,
            color=PINK,
            x_range=[-1.5, 1.5],
            y_range=[-1.2, 1.8],
        )

        # 添加标签
        label = (
            MathTex("(x^2 + y^2 - 1)^3 = x^2 y^3", color=GREEN)
            .shift(DOWN + RIGHT * 1.8)
            .scale(0.6)
        )

        self.play(Create(heart), Write(label))

4. 附件

文中的代码只是关键部分的截取，完整的代码共享在网盘中（implicit_function.py），

下载地址: 完整代码 (访问密码: 6872)