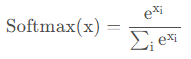SciTech-EECS-BigDataAIML-NN(神经网络): 常用的18种Activation(激活函数)

SciTech-EECS-BigDataAIML-NN(神经网络):

常用的18种Activation(激活函数)

1. 简介
2. 为什么要用激活函数
3. 激活函数的分类
4. 常见的几种激活函数
   
   4.0.Softmax函数
   
   4.1.Sigmoid函数
   
   4.2.Tanh函数
   
   4.3.ReLU函数
   
   4.4.Leaky Relu函数
   
   4.5.PRelu函数
   
   4.6.ELU函数
   
   4.7.SELU函数
   
   4.8.Swish函数
   
   4.9.Mish函数

一：简介

激活函数（Activation Function），就是在人工神经网络的神经元上运行的函数，将神经元的输入映射到输出端，目标帮助网络学习数据的复杂模式。

下图展示了一个神经元是 如何 输入激活函数 以及 如何得到该神经元最终的输出：

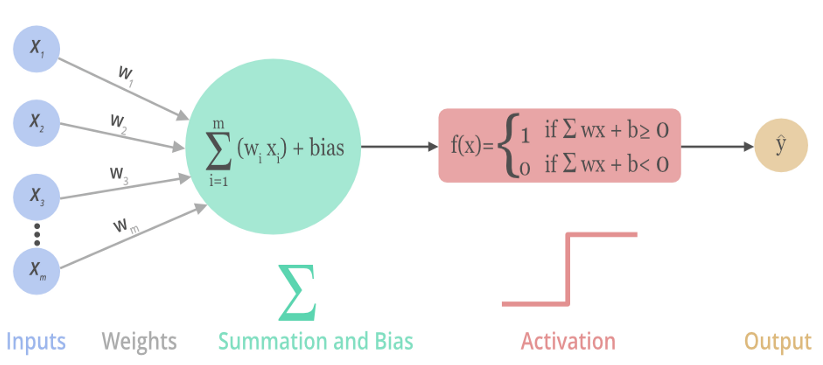
二：为什么要用激活函数

如果不用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，就是最原始的感知机(Perceptron)。

使用激活函数 能够给神经元引入 非线性因素，使神经网络可以任意逼*任何非线性函数，使深层神经网络表达能力更加强大，于是神经网络就可以应用到众多的非线性模型。

三：激活函数的分类

激活函数可以分为两大类：

• 饱和激活函数： sigmoid、 tanh...
• 非饱和激活函数: ReLU 、Leaky Relu 、ELU、PReLU、RReLU...

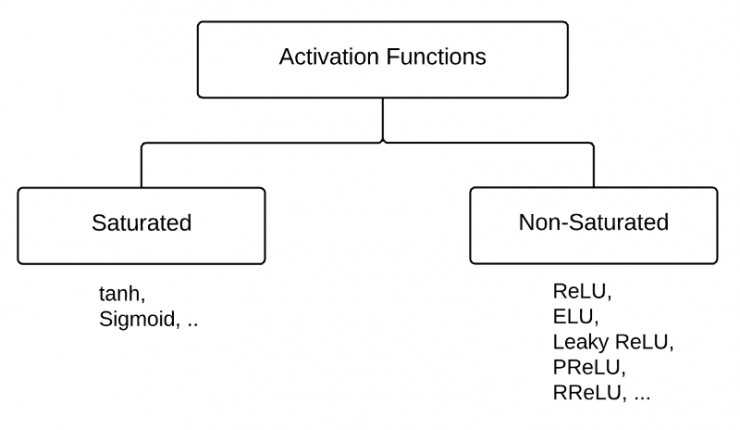
首先，我们先了解一下什么是饱和？

反之，不满足以上条件的函数则称为非饱和激活函数。

• Sigmoid函数需要一个实值输入，压缩至[0,1]的范围
• tanh函数需要讲一个实值输入，压缩至 [-1, 1]的范围

相对于饱和激活函数，使用非饱和激活函数的优势在于两点：

1. 非饱和激活函数能解决深度神经网络（层数非常多）带来的梯度消失问题
2. 使用非饱和激活函数能加快收敛速度。

四：常见的几种激活函数

4.0.Softmax函数

• Softmax激活函数的数学表达式为：
  
  
  
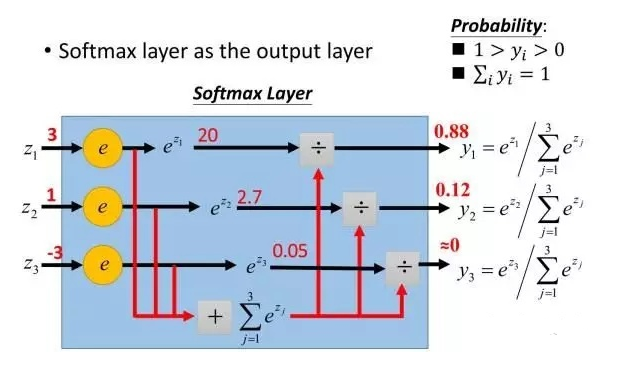
  下图给出 Softmax 对 输出值 的 映射:
  
  
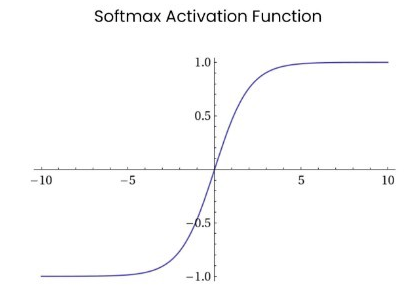
• 函数图像如下:
  
  
• Softmax函数常用作“输出层”当激活函数, 将输出层的值映射到0-1区间，
  
  将神经元输出 构造成概率分布，用于多分类问题，
  
  Softmax激活函数映射值越大，则真实类别可能性越大.

4.1.Sigmoid函数

• Sigmoid激活函数的数学表达式为:
  
  \(\large f(x) = \dfrac{1}{1+e^{-x}}\)

• 导数表达式为:
  
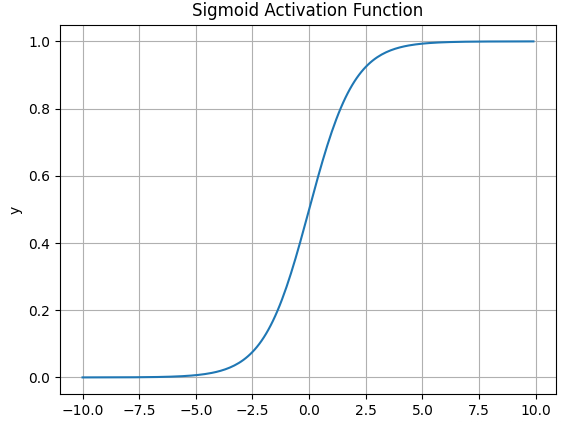
  \(\large f^{'}(x) = f(x)(1-f(x))\)

• 函数图像如下：
  
  

• Sigmoid 函数在历史上曾非常常用，输出值范围为[0,1]之间的实数。
  
  但是现在它已经实际很少使用。

• 什么情况下适合使用Sigmoid？

  • Sigmoid 函数的输出范围是 0 到 1。非常适合作为模型的输出函数用于输出一个0~1范围内的概率值，比如用于表示二分类的类别或者用于表示置信度。
  • 梯度*滑，便于求导，也防止模型训练过程出现突变的梯度.

• Sigmoid有哪些缺点？

  • 容易造成梯度消失。我们由其导函数图像了解到，
    
    sigmoid的导数都是小于0.25的，那么在进行反向传播时，
    
    梯度相乘 结果会步步趋于0，少有梯度信号 通过 神经元 传到 前面层的梯度更新，
    
    因此这时 前面层的权值 几乎没有更新，这就叫梯度消失。
  • 此外，为防止饱和，必须对于权重矩阵的初始化特别留意。
    
    如果初始化权重过大，可能很多神经元得到一个比较小的梯度，
    
    致使神经元不能很好的更新权重提前饱和，神经网络就学习不了。
  • 函数输出 如果不是以 0 为中心的，梯度可能会向特定方向移动，导致降低权重更新的效率。
  • Sigmoid 函数 执行 指数运算，会用到大量计算资源。

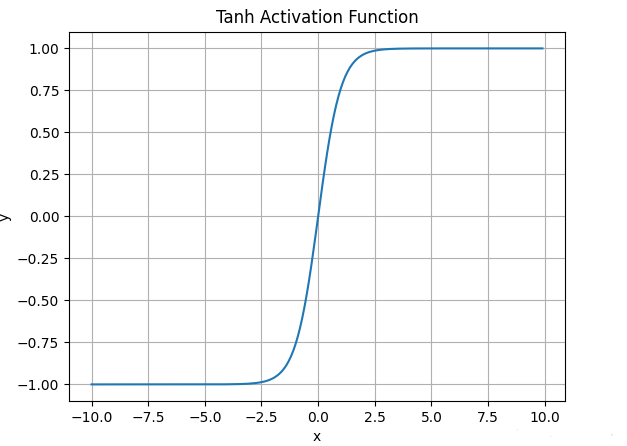
4.2.Tanh函数

• tanh激活函数的数学表达式为：
  
  \(\large f(x) = \dfrac{e^{x} - e^{-x}}{e^{-x} + e^{-x}}\)
  
  实际上，Tanh函数是 sigmoid 的变形：\(\large tanh(x) = 2Sigmoid(2x) - 1\)

• 函数图像如下：
  
  

• 与sigmoid不同的是, tanh是“零为中心”的。
  
  因此在实际应用，tanh会比sigmoid更好一些。
  
  但是在饱和神经元的情况下，tanh还是没有解决梯度消失问题。

• 什么情况下适合使用Tanh？

  • tanh 的输出间隔为 1，并且整个函数以 0 为中心，比 sigmoid 函数更好；
  • 在 tanh 图，负输入将被强映射为负，而零输入被映射为接*零。

• Tanh有哪些缺点？

  • 仍然存在梯度饱和的问题
  • 依然进行的是指数运算

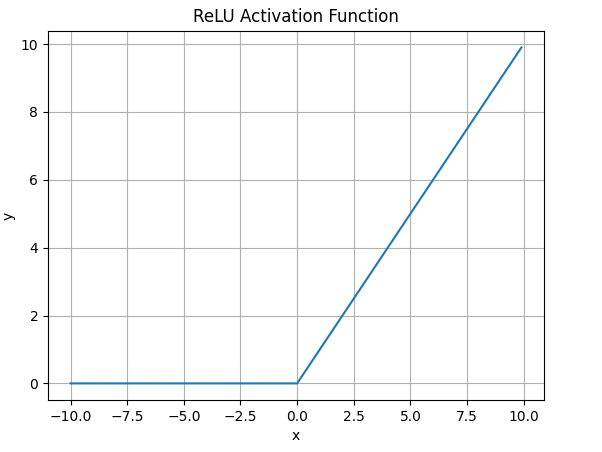
4.3.ReLU函数

• ReLU激活函数的数学表达式为：
  
  \(\large ReLU(x) = max(0,x)\)

• ReLU函数图像如下
  
  

• 什么情况下适合使用ReLU？

  • ReLU解决了梯度消失的问题: 当输入值为正时，神经元不会饱和;
  • ReLU线性、非饱和的性质，在SGD能够快速收敛
  • 计算复杂度低，不需要进行指数运算

• ReLU有哪些缺点？

  • 与Sigmoid一样，其输出不是以0为中心的
  • Dead ReLU 问题。当输入为负时，梯度为0。
    
    这个神经元及之后的神经元的梯度永远为0, 将不响应任何数据，导致相应参数永远不会被更新。训练神经网络时，一旦学习率没有设置好，第一次更新权重时, 输入是负值, 那么这个含有ReLU的神经节点就会死亡，不会被激活。
    
    所以，要设置一个合适的较小的学习率，来降低这种情况的发生.

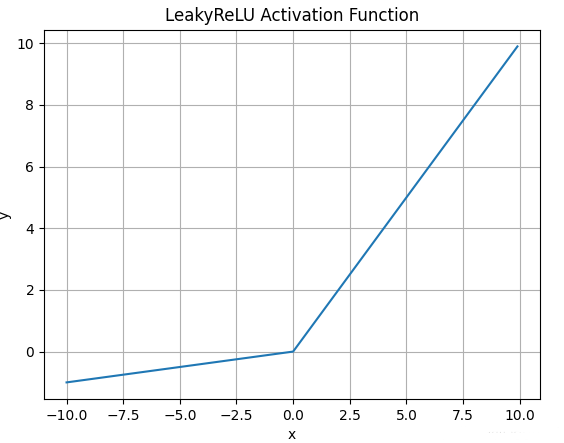
4.4.Leaky Relu函数

• Leaky Relu激活函数的数学表达式为：
  
  \(\large LeakyReLU(x) = max(\alpha x,x)\)
• 函数图像如下：
  
  
• 什么情况下适合使用Leaky ReLU？
  • 解决ReLU输入值为负时神经元死亡的问题
  • Leaky ReLU线性、非饱和的性质，在SGD中能够快速收敛
  • 计算复杂度低，不需要进行指数运算
• Leaky ReLU有哪些缺点？
  
  函数中的α，需要通过先验知识人工赋值（一般设为0.01）
  • 有些*似线性，导致在复杂分类时效果不好。
• 注意：理论上, Leaky ReLU 有 ReLU 的所有优点,
  
  而且 Dead ReLU 不会有任何问题，
  
  但实际上, 尚未完全证明 Leaky ReLU 总比 ReLU 更好.

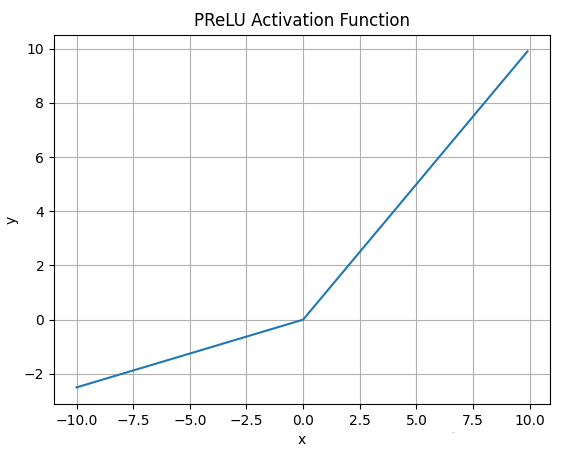
4.5.PRelu函数

• PRelu激活函数的数学表达式为：
  
  \(\large PReLU(\alpha, x) = \begin{cases} \alpha x,\ for \ x < 0 \\ x,\ for \ x >= 0 \end{cases}\)

• 函数图像如下：
  
  

• PRelu也是解决ReLU的神经元坏死问题.
  
  与Leaky ReLU不同: PRelu负半轴的斜率参数α 是学习得到的，而不是人工设置的恒定值.

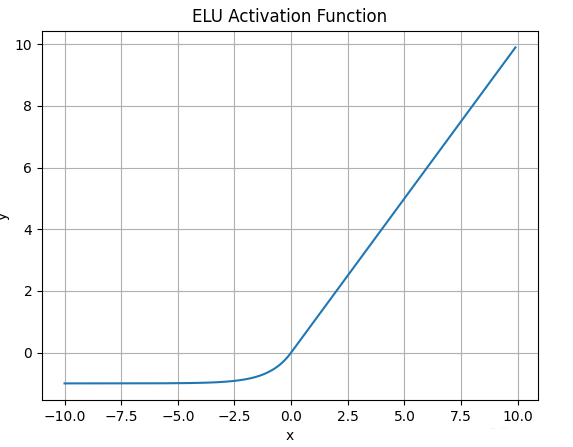
4.6.ELU函数

• ELU激活函数的数学表达式为：
  
  \(\large ELU(\alpha, x) = \begin{cases} \alpha (e^x - 1),\ for \ x <= 0 \\ x,\ for \ x > 0 \end{cases}\)
• 函数图像如下：
  
  
• 与Leaky ReLU和PRelu不同的是，ELU的负半轴是一指数函数, 而不是一条直线.
• 什么情况下适合使用ELU？
  • ELU试图将输出均值接*于零, 使正常梯度更接*于单位自然梯度,加快学习速度.
  • ELU 在较小输入下饱和至负值, 会减少前向传播的变异和信息
• ELU有哪些缺点？
  
  计算的时需要计算指数，计算资源用的多。

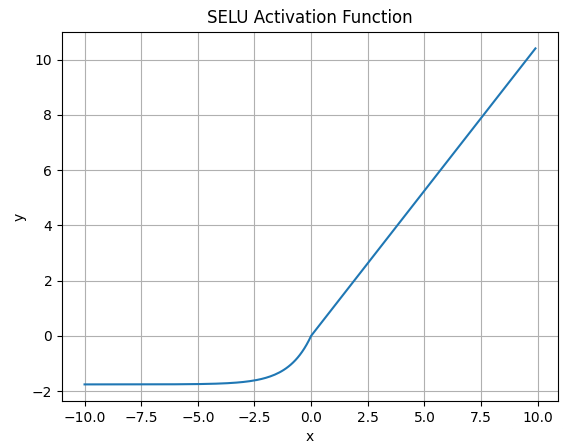
4.7.SELU函数

• SELU激活函数的数学表达式为：
  
  \(\large SELU(\alpha, x) = \lambda \begin{cases} \alpha (e^x - 1),\ for \ x <= 0 \\ x,\ for \ x > 0 \end{cases}\)
  
  其中λ = 1.0507 , α = 1.6733

• 函数图像如下：
  
  

• SELU 允许构建一个映射 g，其性质能够实现 SNN（自归一化神经网络）。SNN 不能通过ReLU、sigmoid 、tanh 和 Leaky ReLU 实现。这个激活函数需要有:

  1. 负值和正值，以便控制均值；
  2. 饱和区域（导数趋*于零），以便抑制更低层的较大方差；
  3. 大于 1 的斜率，以便在更低层中的方差过小时增大方差；
  4. 连续曲线。后者能确保一个固定点，其中方差抑制可通过方差增大来获得均衡。
     
     通过乘上指数线性单元（ELU）来满足激活函数的这些性质，
     
     而且 λ>1 能够确保正值净输入的斜率大于 1

• SELU是在自归一化网络定义的，通过调整均值和方差来实现内部的归一化。
  
  这种内部归一化比外部归一化更快，这使得网络能够更快得收敛

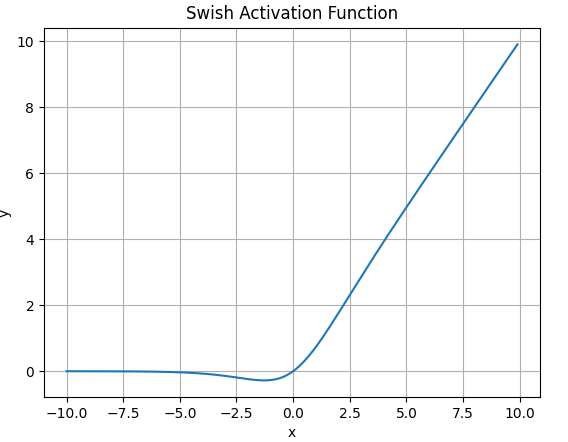
4.8.Swish函数

• Swish激活函数的数学表达式为：
  
  \(\large Swish(x) = x * Sigmoid(x)\)
• 函数图像如下：
  
  
• Swish无界性有助于防止慢训练期间, 梯度渐* 0 并导致饱和；
  
  同时, 有界性也是有优势的, 因为有界激活函数可有很强的正则化(防止过拟合, 进而增强泛化能力), 并且较大的负输入问题也能解决.
• Swish在x=0 附*更为*滑而非单调的特性, 增强了输入数据和要学习的权重的表达能力。

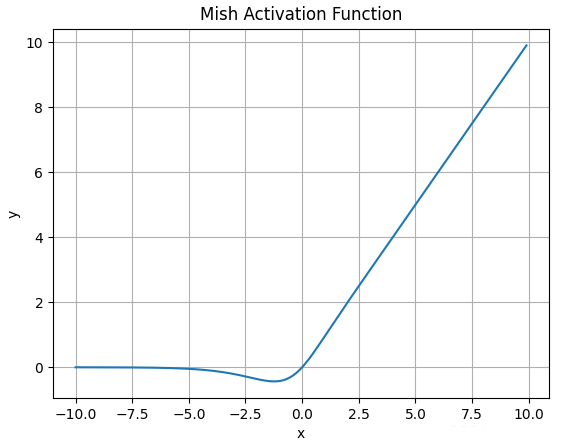
4.9.Mish函数

• Mish激活函数的数学表达式为：
  
  \(\large Mish(x) = x * tanh( ln(1+e^x))\)

• 函数图像如下:
  
  

• Mish的图像与Swish类似, 但要更为*滑，缺点是计算复杂度要更高一些