SciTech-Mathmatics-Probability+Statistics: How to Read and Interpret a $\large Regression\ Table$

How to Read and Interpret a Regression Table

BY ZACH BOBBITTPOSTED ON MARCH 20, 2019

https://www.statology.org/read-interpret-regression-table/

In statistics, regression is a technique that can be used to analyze the relationship between predictor variables and a response variable.

When you use software (like R, SAS, SPSS, etc.) to perform a regression analysis, you will receive a regression table as output that summarize the results of the regression. It's important to know how to read this table so that you can understand the results of the regression analysis.

This tutorial walks through an example of a regression analysis and provides an in-depth explanation of how to read and interpret the output of a regression table.

A Regression Example

Suppose we have the following dataset that shows the total number of hours studied, total prep exams taken, and final exam score received for 12 different students:



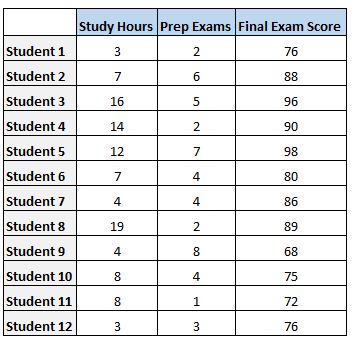
Regression analysis data example

To analyze the relationship between hours studied and prep exams taken with the final exam score that a student receives, we run a multiple linear regression using hours studied and prep exams taken as the \(\large predictor\ variables\) and final exam score as the \(\large response\ variable\).

We receive the following output:

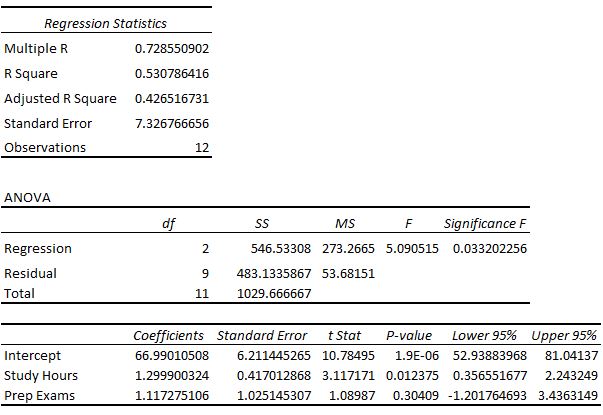
Examining the Fit of the Model

The first section shows several different numbers that measure the fit of the regression model, i.e. how well the regression model is able to "fit" the dataset.

Here is how to interpret each of the numbers in this section:

Multiple R

Multiple R is the square root of R-squared (see below)

This is the \(\large correlation\ coefficient\). It measures the strength of the linear relationship between the predictor variables and the response variable. A multiple R of 1 indicates a perfect linear relationship while a multiple R of 0 indicates no linear relationship whatsoever.

In this example, the multiple R is 0.72855, which indicates a fairly strong linear relationship between the predictors study hours and prep exams and the response variable final exam score.

R-Squared

This is often written as \(\large r^2\), and is also known as the \(\largevcoefficient\ of\ determination\). It is the proportion of the variance in the response variable that can be explained by the predictor variable.

The value for R-squared can range from 0 to 1. A value of 0 indicates that the response variable cannot be explained by the predictor variable at all. A value of 1 indicates that the response variable can be \(\large perfectly\ explained\ without\ error\) by the predictor variable.

In this example, the R-squared is 0.5307, which indicates that 53.07% of the variance in the final exam scores can be explained by the number of hours studied and the number of prep exams taken.

Related: What is a Good R-squared Value?

Adjusted R-Squared

This is a modified version of R-squared that has been adjusted for the number of predictors in the model. It is always lower than the R-squared. The adjusted R-squared can be useful for comparing the fit of different regression models to one another.

In this example, the Adjusted R-squared is 0.4265.

Standard Error of the Regression

The standard error of the regression is the average distance that the observed values fall from the regression line. In this example, the observed values fall an average of 7.3267 units from the regression line.

Related: Understanding the Standard Error of the Regression

Observations

This is simply the number of observations in our dataset. In this example, the total observations is 12.

Testing the Overall Significance of the Regression Model

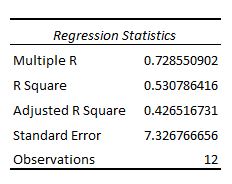
The next section shows the degrees of freedom, the sum of \(\large squares\), \(\large mean\ squares\), \(\large F statistic\), and overall significance of the regression model.

Here is how to interpret each of the numbers in this section:

Regression degrees of freedom

This number is equal to: the number of regression coefficients – 1. In this example, we have an intercept term and two predictor variables, so we have three regression coefficients total, which means the regression degrees of freedom is 3 – 1 = 2.

Total degrees of freedom

This number is equal to: the number of observations – 1. In this example, we have 12 observations, so the total degrees of freedom is 12 – 1 = 11.

Residual degrees of freedom

This number is equal to: total df – regression df. In this example, the residual degrees of freedom is 11 – 2 = 9.

Mean Squares

The regression mean squares is calculated by regression SS / regression df. In this example, regression MS = 546.53308 / 2 = 273.2665.

The residual mean squares is calculated by residual SS / residual df. In this example, residual MS = 483.1335 / 9 = 53.68151.

F Statistic

The f statistic is calculated as regression MS / residual MS. This statistic indicates whether the regression model provides a better fit to the data than a model that contains no independent variables.

In essence, it tests if the regression model as a whole is useful. Generally if none of the predictor variables in the model are statistically significant, the overall F statistic is also not statistically significant.

In this example, the F statistic is 273.2665 / 53.68151 = 5.09.

Significance of F (P-value)

The last value in the table is the p-value associated with the F statistic. To see if the overall regression model is significant, you can compare the p-value to a significance level; common choices are .01, .05, and .10.

If the p-value is less than the significance level, there is sufficient evidence to conclude that the regression model fits the data better than the model with no predictor variables. This finding is good because it means that the predictor variables in the model actually improve the fit of the model.

In this example, the p-value is 0.033, which is less than the common significance level of 0.05. This indicates that the regression model as a whole is statistically significant, i.e. the model fits the data better than the model with no predictor variables.

Testing the Overall Significance of the Regression Model

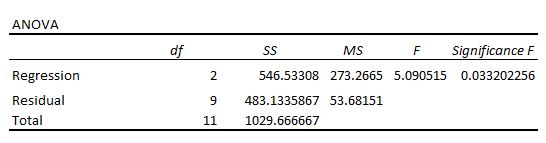
The last section shows the coefficient estimates, the standard error of the estimates, the** t-stat**, p-values, and confidence intervals for each term in the regression model.

Here is how to interpret each of the numbers in this section:

Coefficients

The coefficients give us the numbers necessary to write the estimated regression equation:

\(\large y_hat = b0 + b_1 \mul x_1 + b_2 \mul x_2\).

In this example, the estimated regression equation is:

\(\large \text{final exam score} = 66.99 + 1.299(Study\ Hours) + 1.117(Prep\ Exams)\)

Each individual coefficient is interpreted as the average increase in the response variable for each one unit increase in a given predictor variable, assuming that all other predictor variables are held constant. For example, for each additional hour studied, the average expected increase in final exam score is 1.299 points, assuming that the number of prep exams taken is held constant.

The intercept(截距, 此例是Z轴的) is interpreted as the expected average final exam score for a student who studies for zero hours and takes zero prep exams. In this example, a student is expected to score a 66.99 if they study for zero hours and take zero prep exams. Be careful when interpreting the intercept of a regression output, though, because it doesn't always make sense to do so.

For example, in some cases, the intercept may turn out to be a negative number, which often doesn't have an obvious interpretation. This doesn't mean the model is wrong, it simply means that the intercept by itself should not be interpreted to mean anything.

Standard Error, t-stats, and p-values

The standard error is a measure of the uncertainty around the estimate of the coefficient for each variable.

The t-stat is simply the coefficient divided by the standard error. For example, the t-stat for Study Hours is 1.299 / 0.417 = 3.117.

The next column shows the p-value associated with the t-stat. This number tells us if a given response variable is significant in the model. In this example, we see that the p-value for Study Hours is 0.012 and the p-value for Prep Exams is 0.304. This indicates that Study Hours is a significant predictor of final exam score, while Prep Exams is not.

$\large \text{Confidence Interval for Coefficient Estimates} $

The last two columns in the table provide the lower and upper bounds for \(\large \text{a 95% confidence interval}\) for \(\large \text{the coefficient estimates}\).

• For example, the coefficient estimate for Study Hours is 1.299, but there is some uncertainty around this estimate. We can never know for sure if this is the exact coefficient. Thus, a 95% confidence interval gives us a range of likely values for the true coefficient.

• In this case, the 95% confidence interval for Study Hours is (0.356, 2.24).
  
  Notice that this confidence interval does not contain the number "0", which means we're quite confident that the true value for the coefficient of Study Hours is non-zero, i.e. a positive number.

• By contrast, the 95% confidence interval for Prep Exams is (-1.201, 3.436).
  
  Notice that this confidence interval does **contain the number "0", which means that the true value for the coefficient of Prep Exams could be zero, i.e. non-significant in predicting final exam scores.

Additional Resources

Understanding the Null Hypothesis for Linear Regression

Understanding the F-Test of Overall Significance in Regression

How to Report Regression Results