Boosting算法简介

一、Boosting算法的发展历史
Boosting算法是一种把若干个分类器整合为一个分类器的方法，在boosting算法产生之前，还出现过两种比较重要的将多个分类器整合为一个分类器的方法，即boostrapping方法和bagging方法。我们先简要介绍一下bootstrapping方法和bagging方法。

1）bootstrapping方法的主要过程

主要步骤：

i)重复地从一个样本集合D中采样n个样本

ii)针对每次采样的子样本集，进行统计学习，获得假设Hi

iii)将若干个假设进行组合，形成最终的假设Hfinal

iv)将最终的假设用于具体的分类任务

2）bagging方法的主要过程

主要思路：

i)训练分类器

从整体样本集合中，抽样n* < N个样本 针对抽样的集合训练分类器Ci

ii)分类器进行投票，最终的结果是分类器投票的优胜结果

但是，上述这两种方法，都只是将分类器进行简单的组合，实际上，并没有发挥出分类器组合的威力来。直到1989年，Yoav Freund与 Robert Schapire提出了一种可行的将弱分类器组合为强分类器的方法。并由此而获得了2003年的哥德尔奖（Godel price）。

Schapire还提出了一种早期的boosting算法，其主要过程如下：

i)从样本整体集合D中，不放回的随机抽样n1 < n 个样本，得到集合 D1

训练弱分类器C1

ii)从样本整体集合D中，抽取 n2 < n 个样本，其中合并进一半被 C1 分类错误的样本。得到样本集合 D2

训练弱分类器C2

iii)抽取D样本集合中，C1 和 C2 分类不一致样本，组成D3

训练弱分类器C3

iv)用三个分类器做投票，得到最后分类结果

到了1995年，Freund and schapire提出了现在的adaboost算法，其主要框架可以描述为：

i)循环迭代多次

更新样本分布

寻找当前分布下的最优弱分类器

计算弱分类器误差率

ii)聚合多次训练的弱分类器

在下图中可以看到完整的adaboost算法：

现在，boost算法有了很大的发展，出现了很多的其他boost算法，例如：logitboost算法，gentleboost算法等等。在这次报告中，我们将着重介绍adaboost算法的过程和特性。

二、Adaboost算法及分析
从图1.1中，我们可以看到adaboost的一个详细的算法过程。Adaboost是一种比较有特点的算法，可以总结如下：

1）每次迭代改变的是样本的分布，而不是重复采样（re weight)

2）样本分布的改变取决于样本是否被正确分类

总是分类正确的样本权值低

总是分类错误的样本权值高（通常是边界附近的样本）

3）最终的结果是弱分类器的加权组合

权值表示该弱分类器的性能

简单来说，Adaboost有很多优点:

1)adaboost是一种有很高精度的分类器

2)可以使用各种方法构建子分类器，adaboost算法提供的是框架

3)当使用简单分类器时，计算出的结果是可以理解的。而且弱分类器构造极其简单

4)简单，不用做特征筛选

5)不用担心overfitting！

总之：adaboost是简单，有效。

下面我们举一个简单的例子来看看adaboost的实现过程：

图中，“+”和“-”分别表示两种类别，在这个过程中，我们使用水平或者垂直的直线作为分类器，来进行分类。

第一步：

根据分类的正确率，得到一个新的样本分布D2­，一个子分类器h1

其中划圈的样本表示被分错的。在右边的途中，比较大的“+”表示对该样本做了加权。

第二步：

根据分类的正确率，得到一个新的样本分布D3，一个子分类器h2

第三步：

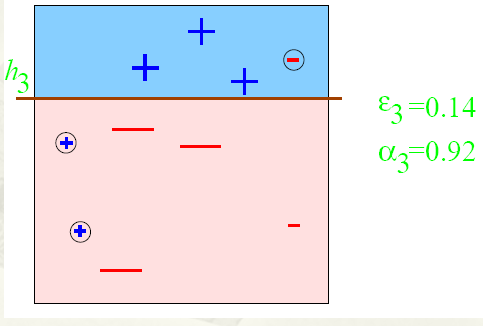
得到一个子分类器h3

整合所有子分类器：

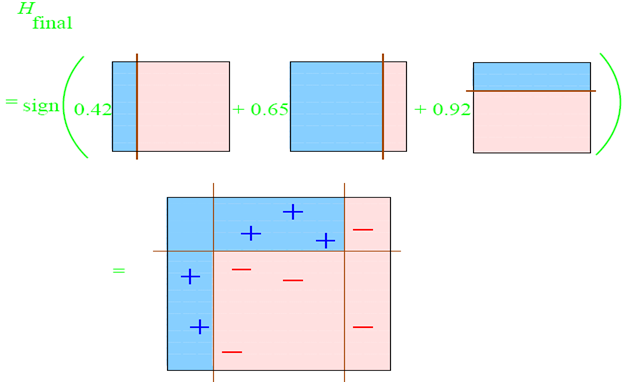
因此可以得到整合的结果，从结果中看，及时简单的分类器，组合起来也能获得很好的分类效果，在例子中所有的。 
Adaboost算法的某些特性是非常好的，在我们的报告中，主要介绍adaboost的两个特性。一是训练的错误率上界，随着迭代次数的增加，会逐渐下降；二是adaboost算法即使训练次数很多，也不会出现过拟合的问题。

下面主要通过证明过程和图表来描述这两个特性：

1）错误率上界下降的特性

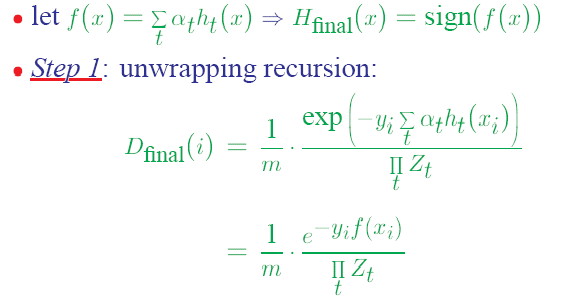
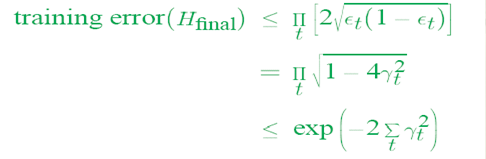
从而可以看出，随着迭代次数的增加，实际上错误率上界在下降。

2）不会出现过拟合现象

通常，过拟合现象指的是下图描述的这种现象，即随着模型训练误差的下降，实际上，模型的泛化误差（测试误差）在上升。横轴表示迭代的次数，纵轴表示训练误差的值。

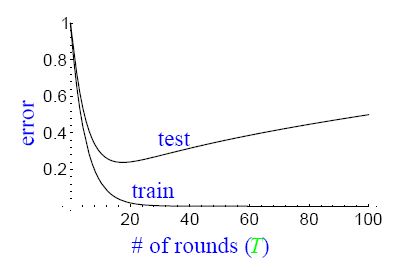
而实际上，并没有观察到adaboost算法出现这样的情况，即当训练误差小到一定程度以后，继续训练，返回误差仍然不会增加。

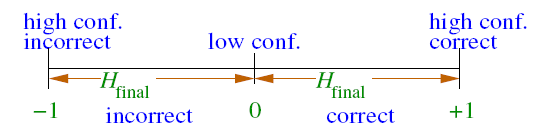
对这种现象的解释，要借助margin的概念，其中margin表示如下：

通过引入margin的概念，我们可以观察到下图所出现的现象：

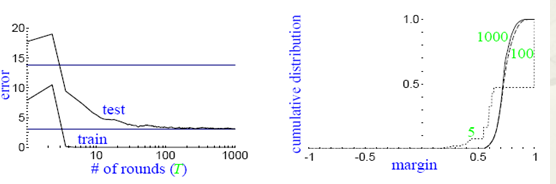
从图上左边的子图可以看到，随着训练次数的增加，test的误差率并没有升高，同时对应着右边的子图可以看到，随着训练次数的增加，margin一直在增加。这就是说，在训练误差下降到一定程度以后，更多的训练，会增加分类器的分类margin，这个过程也能够防止测试误差的上升。

三、多分类adaboost
在日常任务中，我们通常需要去解决多分类的问题。而前面的介绍中，adaboost算法只能适用于二分类的情况。因此，在这一小节中，我们着重介绍如何将adaboost算法调整到适合处理多分类任务的方法。

目前有三种比较常用的将二分类adaboost方法。

1、adaboost M1方法

主要思路： adaboost组合的若干个弱分类器本身就是多分类的分类器。

在训练的时候，样本权重空间的计算方法，仍然为：

在解码的时候，选择一个最有可能的分类

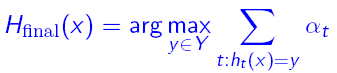
2、adaboost MH方法

主要思路： 组合的弱分类器仍然是二分类的分类器，将分类label和分类样例组合，生成N个样本，在这个新的样本空间上训练分类器。

可以用下图来表示其原理：

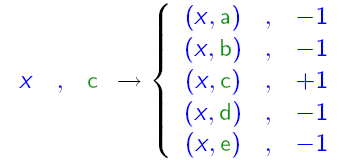
3、对多分类输出进行二进制编码

主要思路：对N个label进行二进制编码，例如用m位二进制数表示一个label。然后训练m个二分类分类器，在解码时生成m位的二进制数。从而对应到一个label上。

四、总结
最后，我们可以总结下adaboost算法的一些实际可以使用的场景：

1）用于二分类或多分类的应用场景

2）用于做分类任务的baseline

无脑化，简单，不会overfitting，不用调分类器

3）用于特征选择（feature selection)

4）Boosting框架用于对badcase的修正

只需要增加新的分类器，不需要变动原有分类器

由于adaboost算法是一种实现简单，应用也很简单的算法。Adaboost算法通过组合弱分类器而得到强分类器，同时具有分类错误率上界随着训练增加而稳定下降，不会过拟合等的性质，应该说是一种很适合于在各种分类场景下应用的算法。