JavaScript中国象棋程序（3） - 电脑自动走棋

“JavaScript中国象棋程序” 这一系列教程将带你从头使用JavaScript编写一个中国象棋程序。这是教程的第3节。

程序的最终效果点击这里查看。

这一系列共有9个部分：

0、JavaScript中国象棋程序（0）- 前言

1、JavaScript中国象棋程序（1）- 界面设计

2、JavaScript中国象棋程序（2）- 校验棋子走法 

3、JavaScript中国象棋程序（3）- 电脑自动走棋

4、JavaScript中国象棋程序（4）- 极大极小搜索算法

5、JavaScript中国象棋程序（5）- Alpha-Beta搜索

6、JavaScript中国象棋程序（6）- 克服水平线效应、检查重复局面

7、JavaScript中国象棋程序（7）- 置换表

8、JavaScript中国象棋程序（8）- 进一步优化

这一节，程序将可以自动行棋。但仅仅是走了一步符合象棋规则的棋，电脑智商为0。

3.1、帅（将）的走法生成

使用一个辅助数值表示这4个方向：

var KING_DELTA = [-16, -1, 1, 16];

已知帅在一维棋局数组中的起点位置sqSrc。生成帅的走法，就是获取帅全部的合法终点sqDes。使用一个数组存储所有可能的走法，伪代码如下：

for (var i = 0; i < 4; i ++) {		// 将的4个方向
  var sqDst = sqSrc + KING_DELTA[i];	// 得到一个可能的终点位置
  if (该位置不位于九宫中) {
    // 该走法不合法，执行下一轮循环
    continue;
  }
  var pcDst = 终点位置的棋子;	　　　　// 如果终点位置没有棋子，那么pcDst=0
  if (pcDst不是本方棋子) {
    走法合法，保存到步骤数组中
  }
}

3.2、仕的走法生成

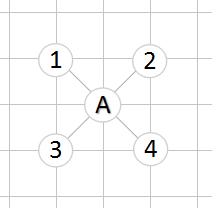
同样使用辅助数组表示仕的4个方向：

var ADVISOR_DELTA = [-17, -15, 15, 17];

生成仕的走法，伪代码如下：

for (var i = 0; i < 4; i ++) {　　　　　　// 仕的4个方向
  var sqDst = sqSrc + ADVISOR_DELTA[i];	// 得到一个可能的终点位置
  if (该位置不位于九宫中) {
    // 该走法不合法，执行下一轮循环
    continue;
  }
  var pcDst = 终点棋子;　　　　　　　　　　// 如果终点位置没有棋子，那么pcDst=0
  if (pcDst不是本方棋子) {
    走法合法，保存到步骤数组中
  }
}

3.3、象的走法生成

我们并不用设置一个类似[-34, -30, 30, 37]的数组保存象的方向。因为仕的方向，跟象眼的方向一致。仕方向的二倍，就是象的方向。

生成象的走法，伪代码如下：

for (var i = 0; i < 4; i ++) {		// 象的4个方向
  var sqDst = sqSrc + ADVISOR_DELTA[i];	// 获得象眼的位置
  if (象眼不在棋盘上，或者象眼位置已过河，或者象眼存在棋子) {
    	// 位置不合法，执行下一轮循环
	continue;
  }
  sqDst += ADVISOR_DELTA[i];	　　　　// 得到一个可能的终点位置
  var pcDst = 终点位置的棋子	　　　　// 如果终点位置没有棋子，那么pcDst=0
  if (pcDst不是本方棋子) {
    走法合法，保存到步骤数组中
  }
}

3.4、马的走法生成

用辅助数组表示马的方向：

KNIGHT_DELTA = [[-33, -31], [-18, 14], [-14, 18], [31, 33]];

对应马腿的4个方向，与帅的4个方向是一样的。

生成马的走法，伪代码如下：

for (var i = 0; i < 4; i ++) {　　　　　　// 马腿的4个方向
  var sqDst = sqSrc + KING_DELTA[i];　　// 得到一个马腿的位置
  if (马腿位置存在棋子) {
    continue;
  }
  for (var j = 0; j < 2; j ++) {	// 1个马腿对应2个马的方向
    sqDst = sqSrc + KNIGHT_DELTA[i][j];	// 得到一个马的可能的终点位置
    if (该位置不在棋盘上) {
      continue;
    }
    var pcDst = 终点位置的棋子;		// 如果终点位置没有棋子，那么pcDst=0
    if (pcDst不是本方棋子) {
      走法合法，保存到步骤数组中
    }
  }
}

3.5、车的走法生成

车的方向与帅的方向相同，只不过车可以连续走下去。

生成车的走法，伪代码如下：

for (var i = 0; i < 4; i ++) {
  var delta = KING_DELTA[i];	// 得到一个方向
  var sqDst = sqSrc + delta;	// 从起点sqSrc开始，沿着方向delta走一步
  while (sqDst在棋盘上) {
    var pcDst = sqDst位置的棋子;
    if (pcDst == 0) {		// sqDst位置上根本就没有棋子
      走法合法，保存到步骤数组中
    } else {
      if (pcDst是对方的棋子) {
        走法合法，保存到步骤数组中
      }
      // 已经遇到了对方棋子，终止循环
      break;
    }
    sqDst += delta;		// 沿着方向delta向前走一步
  }
}

3.6、炮的走法生成

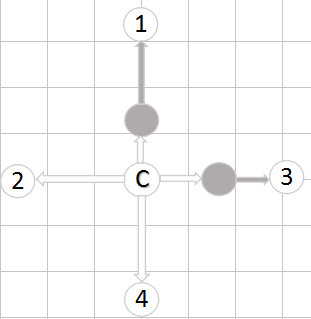
炮的走法与车类似，但炮遇到一个棋子后，可以越过去，也就是翻山，并吃掉一个对方棋子。

生成炮的走法，伪代码如下：

for (var i = 0; i < 4; i ++) {
  var delta = KING_DELTA[i];	// 得到一个方向
  var sqDst = sqSrc + delta;	// 从起点sqSrc开始，沿着方向delta走一步
  while (sqDst在棋盘上) {
    var pcDst = sqDst位置的棋子;
    if (pcDst == 0) {		// sqDst位置上根本就没有棋子
      走法合法，保存到步骤数组中
    } else {			// 终点存在棋子，炮需要翻山
      break;
    }
    sqDst += delta;		// 沿着方向delta向前走一步
  }
  sqDst += delta;		// 沿着方向delta向前走一步
  while (IN_BOARD(sqDst)) {	// 如果sqDst仍位于棋盘，那么此时炮已经翻山了
    var pcDst = sqDst位置的棋子;
    if (pcDst > 0) {		// 炮翻山后遇到了一个棋子
      if (pcDst是对方棋子) {
        走法合法，保存到步骤数组中
      }
      // 炮翻山后，不管遇到的是对方棋子，还是己方棋子，都要结束对当前方向的搜索
      break;
    }
    sqDst += delta;
  }
}

七、兵的走法生成

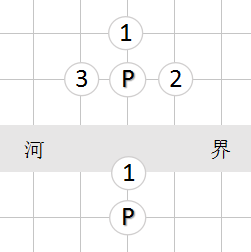
红兵和黑卒向前走的方向是不一样的，分别是-16和16。在上一节，我们已经介绍了下面的函数：

// sp是棋子位置，sd是走棋方（红方0，黑方1）。返回兵（卒）向前走一步的位置。
function SQUARE_FORWARD(sq, sd) {
  return sq - 16 + (sd << 5);
}

该函数可以获得兵（卒）前进一步的位置。

生成兵的走法，伪代码如下：

var sqDst = SQUARE_FORWARD(sqSrc, this.sdPlayer);	// 得到兵（卒）前进一步的位置
if (sqDst在棋盘上) {
  var pcDst = sqDst位置的棋子;
  if (pcDst不是本方棋子) {
    走法合法，保存到步骤数组中
  }
}
if (这个兵（卒）已过河) {
  for (var delta = -1; delta <= 1; delta += 2) {
    // delta只能取-1和1两个值，这正是兵（卒）的左右两个方向
    sqDst = sqSrc + delta;
    if (sqDst在棋盘上) {
      var pcDst = sqDst位置的棋子;
      if (pcDst不是本方棋子) {
        走法合法，保存到步骤数组中
      }
    }
  }
}

3.8、电脑先走功能的实现

如果我们选择了“电脑先走”，并点击“重新开始”按钮，那么电脑会执红先走。红棋显示在上方，黑棋显示再下方，并且红棋会先走一步，如下图所示：

这其实就是在视觉上，将原来的棋盘旋转180°。例如，本来显示在左上角的黑车，现在显示在右下角的位置。在一维棋盘数组中，左上角的位置是51，右下角的位置是203。也就是说，要想实现对棋盘旋转180°，只需将sq位置的棋子，显示在254-sq的位置。如下函数就是实现这一功能的：

function SQUARE_FLIP(sq) {
  return 254 - sq;
}

当用户点击棋盘时，需要对点击的位置再执行一次SQUARE_FLIP函数，就可以转换为用户点击的棋盘数组中的位置。

3.9、核心代码说明

本节的代码可以在 Github 下载，也可以直接clone

git clone -b step-3 https://github.com/Royhoo/write-a-chinesechess-program

这一节我们引入一个新的对象Search，负责实现搜索算法。目前我们的搜索算法很简单，就是生成全部走法后随机选择一个。

Board中新增或修改的主要属性和方法

（1）、computer

computer = 0，表示电脑执黑；computer = 1，表示电脑执红。在index.html中，会对computer赋初值为0。

（2）、busy

busy默认为false，此时可以响应用户的点击事件。如果电脑正常思考状态下，比如正常执行搜索算法，busy会被置为true，不响应点击事件。

（3）、response()

电脑回一步棋。

（4）、restart(fen)

重新使用fen串初始化棋局。该方法会调用response()，这就实现了在电脑执红的情况下，电脑先走一步棋的功能。

（5）、retract()

悔棋。

Position中新增或修改的主要属性和方法

（1）、mvList[]

这是一个数组，保存每步的走法。悔棋的时候会用到。

（2）、pcList[]

这也是一个数组，保存每步被吃的棋子。如果这一步没有棋子被吃，那么保存的是0。

该数组也会在悔棋的时候用到。

（3）、generateMoves()

生成棋局的所有走法。

（4）、makeMove(mv)

走一步棋，主要需要以下4步：

1、删除终点棋子，并记录吃子。

2、将起点棋子放在终点。

3、保存这一走法。

4、切换走棋方。

Search中主要属性和方法

（1）、pos

Position实例。

（2）、searchMain（）

搜索算法。目前非常简单，就是生成所有可能的走法，随机选择一个。