算法训练 安慰奶牛(节点有权值的MST)

问题描述

Farmer John变得非常懒，他不想再继续维护供奶牛之间供通行的道路。道路被用来连接N个牧场，牧场被连续地编号为1到N。每一个牧场都是一个奶牛的家。FJ计划除去P条道路中尽可能多的道路，但是还要保持牧场之间 的连通性。你首先要决定那些道路是需要保留的N-1条道路。第j条双向道路连接了牧场Sj和Ej(1 <= Sj <= N; 1 <= Ej <= N; Sj != Ej)，而且走完它需要Lj的时间。没有两个牧场是被一条以上的道路所连接。奶牛们非常伤心，因为她们的交通系统被削减了。你需要到每一个奶牛的住处去安慰她们。每次你到达第i个牧场的时候(即使你已经到过)，你必须花去Ci的时间和奶牛交谈。你每个晚上都会在同一个牧场(这是供你选择的)过夜，直到奶牛们都从悲伤中缓过神来。在早上 起来和晚上回去睡觉的时候，你都需要和在你睡觉的牧场的奶牛交谈一次。这样你才能完成你的 交谈任务。假设Farmer John采纳了你的建议，请计算出使所有奶牛都被安慰的最少时间。

输入格式

第1行包含两个整数N和P。

接下来N行，每行包含一个整数Ci。

接下来P行，每行包含三个整数Sj, Ej和Lj。

输出格式

输出一个整数, 所需要的总时间(包含和在你所在的牧场的奶牛的两次谈话时间)。

样例输入

5 6
10
10
20
6
30
1 2 5
2 3 5
2 4 12
3 4 17
2 5 15
3 5 6

样例输出

178

数据规模与约定

5 <= N <= 10000，N-1 <= P <= 100000，0 <= Lj <= 1000，1 <= Ci <= 1,000。

分析

这个题，与最普通的生成树不一样，根据题意分析，每个节点是有权值的，而且，经过一条边，势必经过他的两个节点一次，他的边两次。

所以边a(1-2)的权值可以写为  W(a) = w(1) + w(2) + 2 * w(a)

另外，题意要求，我们自己找起始点，使得所花时间最少，分析后可以发现，只有起始点，才会多走一次。

举个例子

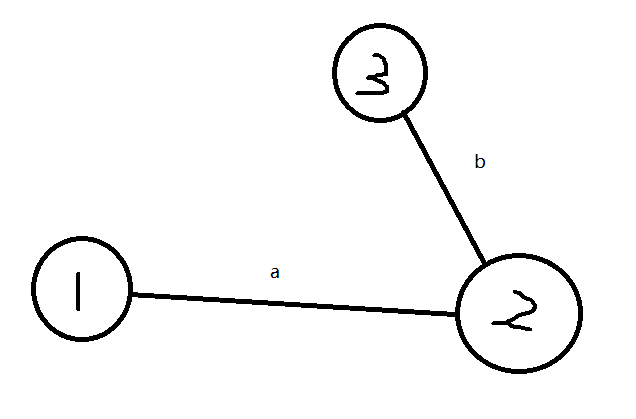
假设①为起始点，那么T = w(1) + w(a) + w(2) + w(b) + w(3) + w(b) + w(2) + w(a) + w(1)

　　　　　　　　　　　=W(a) + W(b) + w(1)

所以起始点，应设为，权值最小的节点。

#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
struct edge{
    int a,b;
    int w;
}; 

int v[];//点的权值

edge se[];//储存边 

int set[];//辅助集合 

int n,p;//顶点个数  边数 

long long sum = ;

long long min_w = ;

bool cmp(edge a,edge b){
    return a.w<b.w;
}
int find(int x){
    return set[x] == x ? x : set[x] = find(set[x]);
}
void hoge(){
    scanf("%d %d",&n,&p);
    for(int i=; i <= n; i++){
        scanf("%d",&v[i]);//录入每个点的权值
        if(v[i] < min_w)
            min_w = v[i];
        set[i] = i; //使每个顶点独自位于一个集合中
    }
    for(int i=;i <= p;i++){
        int a;
        int b;
        int w;
        scanf("%d %d %d",&a,&b,&w);
        w = *w + v[a] + v[b];
        //录入边的信息
        se[i].a = a;
        se[i].b = b;
        se[i].w = w;

    }
    sort(se+,se+p+,cmp);
    int num = ;// num表示边的序号
    int k = ;// k表示已有几个边在子图中
    while(k <= n-){
        int a = find(se[num].a);
        int b = find(se[num].b);
        if(a != b){
            k++;//子图中加入一条边
            sum +=se[num].w;
            set[b] = a;
        }
        num++;
    }
}
int main(){
    hoge();
    sum = sum + min_w;
    cout<<sum;
    return ;
}