NB二人组（一）----堆排序

堆排序前传--树与二叉树简介

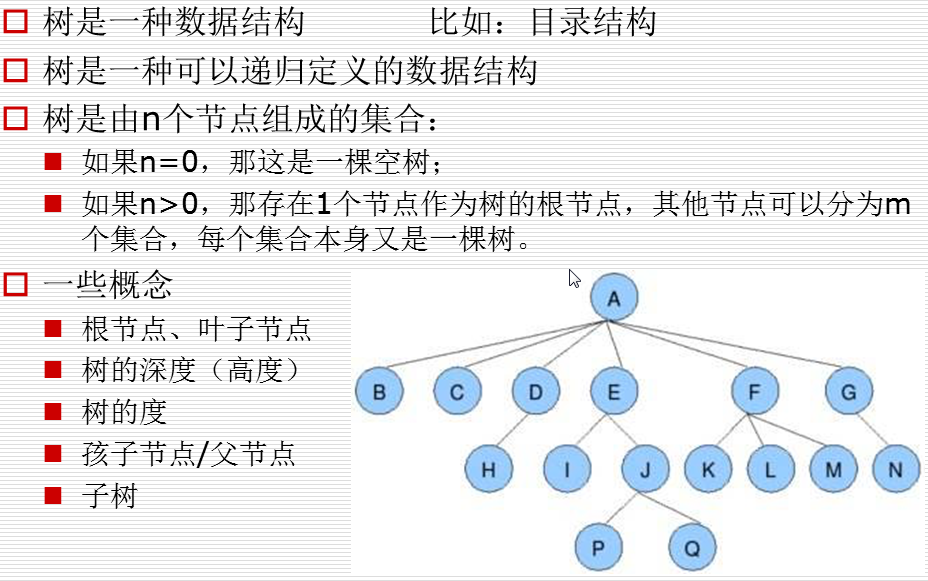
特殊且常用的树--二叉树 

两种特殊的二叉树

二叉树的存储方式

二叉树小结

堆排序

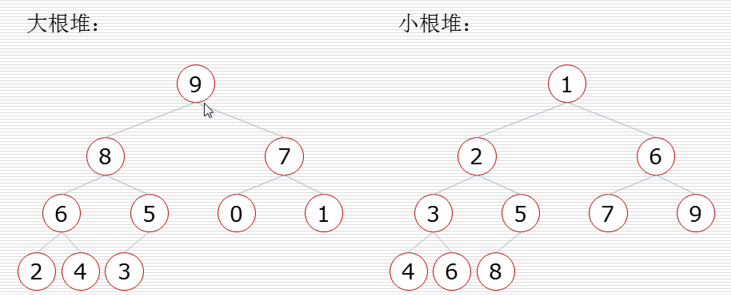
堆这个玩意.......

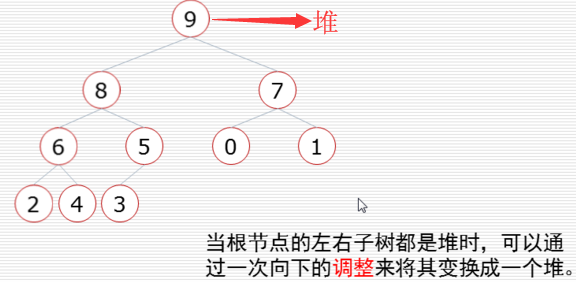
堆排序过程：

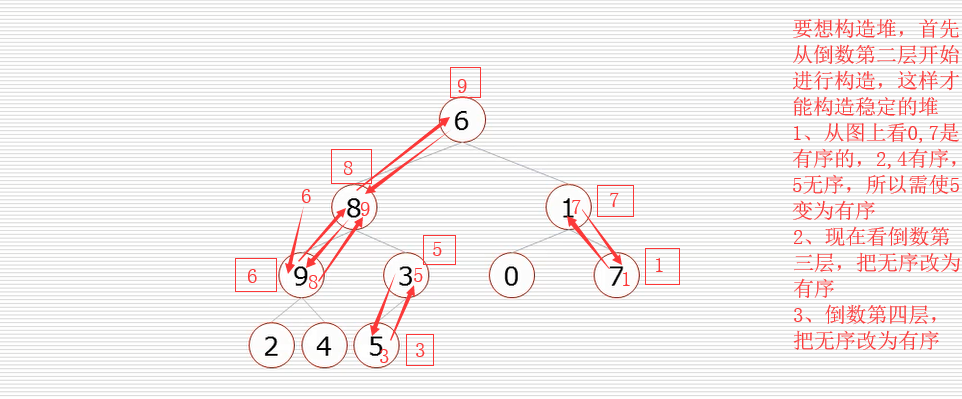
构造堆：

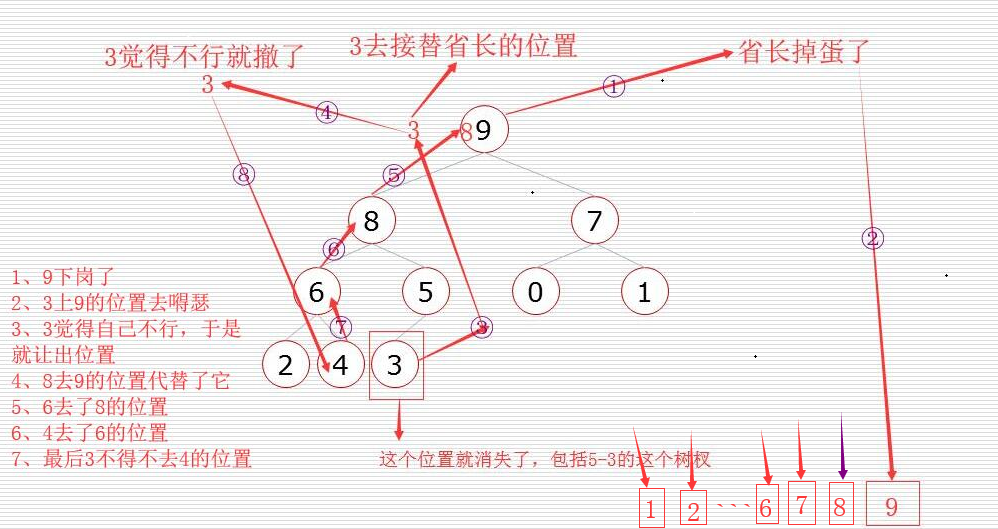
堆排序的算法程序(程序需配合着下图理解)：

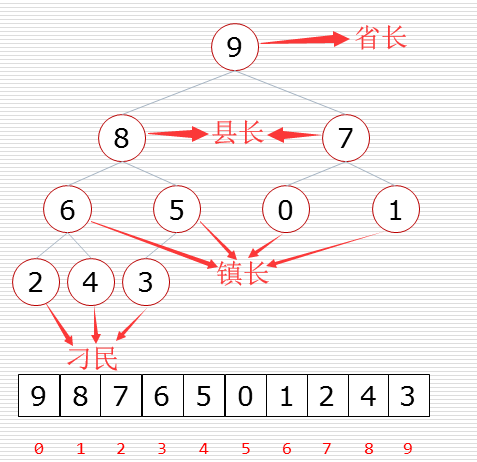
def sift(data,low,high):   # 调整函数
    i = low  # 树的根  也就是父亲 ，这里只领导
    j = 2 * i + 1 # 根的左孩子 也就是 儿子 ，这里指小领导
    tmp = data[i]  # 把根 取出来 做调整 ， 在这里 领导
    while j <= high:  # high其实就是 根的右儿子（也就是最后一个儿子），如果 j= high 则表示没有右儿子，也就是说这里必须有儿子在
        if j < high and data[j] < data[j + 1]: # j < high 代表有右儿子 ， data[j] < data[j + 1] 说明右儿子比左儿子大
            j += 1 # 这个 j 则变为右儿子 ，也就是 若有比 j 大的值，则 j 就变为比他大的那个值
        if tmp < data[j]: # 如果领导不能干
            data[i] = data[j] # 则小领导上位
            i = j # 小领导变为大领导
            j = 2 * i + 1 # 小小领导变为小领导
        else: # 如果领导能干
            break # 那就待着吧
        data[i] = tmp # 到最后 i 这里肯定会有空位 ，所以无论 tem 是谁 都要占住这个空位

# 方法一
def heap_sort(data):  # 开始进行堆排序
    n = len(data) # n 为长度
    # 开始建堆
    for i in range(n // 2 - 1,-1,-1): # n//2-1为图片中的 5 的位置，-1 为到0 结束 ，-1 为步长
        sift(data,i,n-1) # i 为low也就是其父节点，n-1 为high 也就是堆的最后 ，也就是每次调整小领导所在的堆
    # 堆建好了
    # 升序排列
    for i in range(n-1,-1,-1): # n-1为high 也就是从堆得最后 一直到 0为止，也就是从刁民到领导
        data[0],data[i]=data[i],data[0] # 堆的顶部 和 堆的末尾 互换， 也就是领导退休，刁民上位
        sift(data,0,i-1) # 0 代表着领导 ，i-1 代表着这个堆的位置不能把领导算在内了，也就是领导退休了，把他赶出这个城市了
    # 降序排列，耗内存

# 方法二 耗内存
# def heap_sort(data):  # 开始进行堆排序
#     n = len(data)  # n 为长度
#     # 开始建堆
#     for i in range(n // 2 - 1, -1, -1):  # n//2-1为图片中的 5 的位置，-1 为到0 结束 ，-1 为步长
#         sift(data, i, n - 1)  # i 为low也就是其父节点，n-1 为high 也就是堆的最后 ，也就是每次调整小领导所在的堆
#     # 堆建好了
#     # 降序排列
#     li=[] # 监狱
#     for i in range(n-1,-1,-1):
#         li.append(data[0]) # 领导进监狱了
#         data[i] = data[0] # 领导下位了
#         sift(data,0,i-1)   # 领导离开了城市 ， 进监狱了

 堆的应用

☆☆☆☆堆模块库地址（点击这行字）☆☆☆☆

利用堆模块来进行演算

import heapq # 堆模块
heap = []
data = list(range(10000))
random.shuffle(data)
for i in data:
    heapq.heappush(heap,i)
for i in range(len(heap)):
    print(heapq.heappop(heap))

print(heapq.nlargest(10,data))  # 堆模块 从大到小 排序 只取前十个数
print(heapq.nsmallest(10,data))  # 堆模块 从小到大 排序 只取前十个数

程序演示：

`

`

`