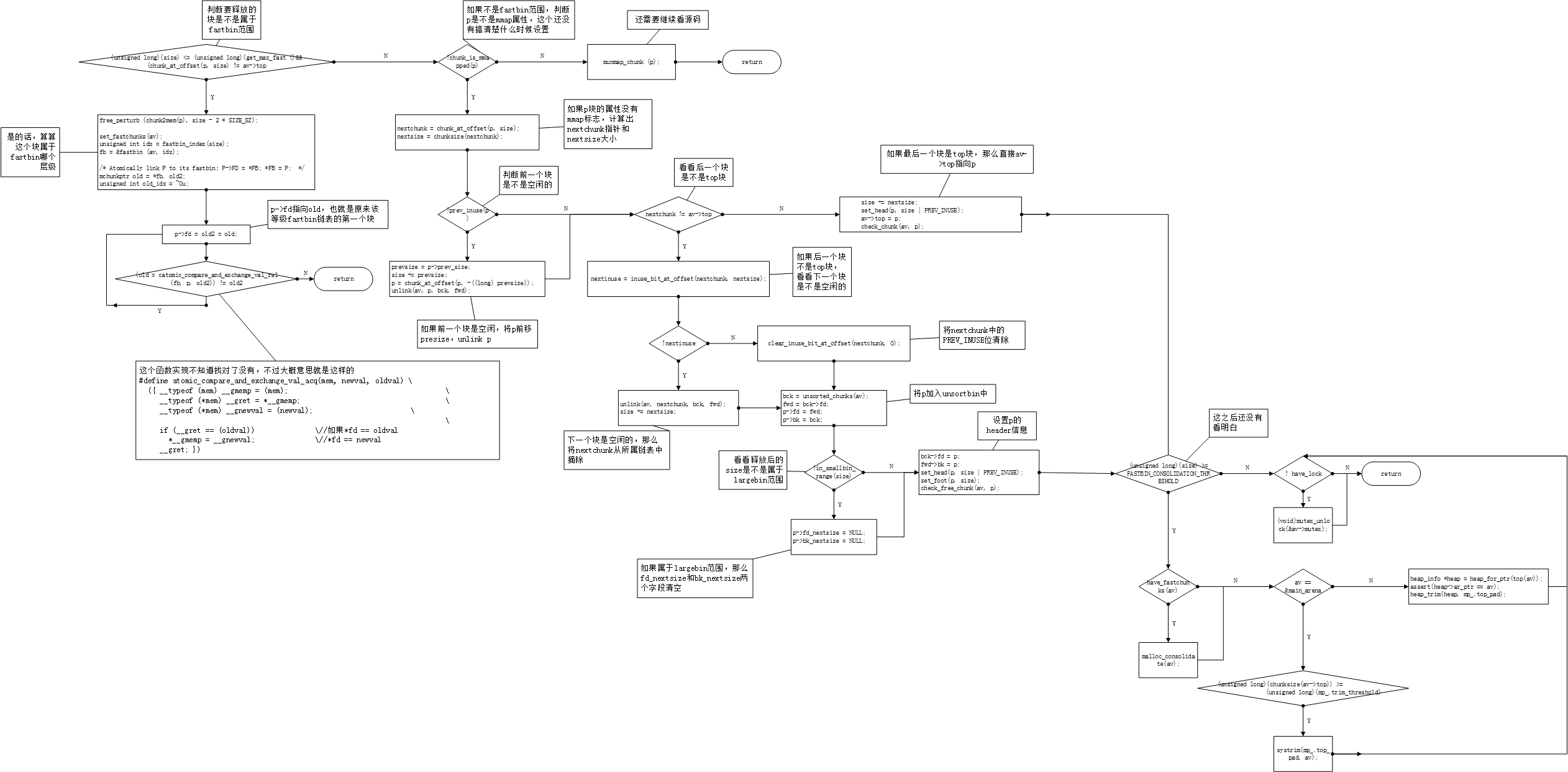
glibc-2.23_int_free_流程浅析
glibc-2.23_int_free_流程浅析的更多相关文章
- GCC编译流程浅析
GCC-GCC编译流程浅析 序言 对于大多数程序员而言,大家都知道gcc是什么,但是如果不接触到linux平台下的开发,鲜有人真正了解gcc的编译流程,因为windows+IDE的开发模式简直是一条龙 ...
- 玩转Windows服务系列——服务运行、停止流程浅析
通过研究Windows服务注册卸载的原理,感觉它并没有什么特别复杂的东西,Windows服务正在一步步退去它那神秘的面纱,至于是不是美女,大家可要睁大眼睛看清楚了. 接下来研究一下Windows服务的 ...
- Android 4.4 Kitkat Phone工作流程浅析(六)__InCallActivity显示更新流程
本文来自http://blog.csdn.net/yihongyuelan 转载请务必注明出处 本文代码以MTK平台Android 4.4为分析对象,与Google原生AOSP有些许差异,请读者知悉. ...
- 玩转Windows服务系列——服务运行、停止流程浅析
原文:玩转Windows服务系列——服务运行.停止流程浅析 通过研究Windows服务注册卸载的原理,感觉它并没有什么特别复杂的东西,Windows服务正在一步步退去它那神秘的面纱,至于是不是美女,大 ...
- PHP容器--Pimple运行流程浅析
需要具备的知识点 闭包 闭包和匿名函数在PHP5.3.0中引入的. 闭包是指:创建时封装周围状态的函数.即使闭包所处的环境不存在了,闭包中封装的状态依然存在. 理论上,闭包和匿名函数是不同的概念.但是 ...
- Android 4.4 Kitkat Phone工作流程浅析(八)__Phone状态分析
本文来自http://blog.csdn.net/yihongyuelan 转载请务必注明出处 本文代码以MTK平台Android 4.4为分析对象.与Google原生AOSP有些许差异.请读者知悉. ...
- Android 4.4 Kitkat Phone工作流程浅析(七)__来电(MT)响铃流程
本文来自http://blog.csdn.net/yihongyuelan 转载请务必注明出处 本文代码以MTK平台Android 4.4为分析对象,与Google原生AOSP有些许差异,请读者知悉. ...
- 以太网驱动的流程浅析(一)-Ifconfig主要流程【原创】
以太网驱动的流程浅析(一)-Ifconfig主要流程 Author:张昺华 Email:920052390@qq.com Time:2019年3月23日星期六 此文也在我的个人公众号以及<Lin ...
- 以太网驱动的流程浅析(三)-ifconfig的-19错误最底层分析【原创】
以太网驱动流程浅析(三)-ifconfig的-19错误最底层分析 Author:张昺华 Email:920052390@qq.com Time:2019年3月23日星期六 此文也在我的个人公众号以及& ...
随机推荐
- Spring学习11-Spring使用proxool连接池 管理数据源
Spring 一.Proxool连接池简介及其配置属性概述 Proxool是一种Java数据库连接池技术.是sourceforge下的一个开源项目,这个项目提供一个健壮.易用的连接池,最为关键的是 ...
- pycharm设置安装python第三方插件
pycharm设置安装python第三方插件 转载于:https://www.mindg.cn/?p=80 今天下了一个pycharm,设置用它来安装python插件,以下是安装步骤,与大家分享,我的 ...
- la4730(并查集+树状数组)
https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&category=30& ...
- python操作word之pywin32的安装
PyCharm 2016.2 官网中文汉化破解版 注册码 http://idea.lanyus.com/ 首先下载安装win32com,下载32位的,不然安装的时候可能检测不到python https ...
- 第二百五十七节,Tornado框架-路由映射,逻辑处理,文件归类配置
Tornado框架-路由映射,逻辑处理,文件归类配置 Tornado框架 Tornado 是 FriendFeed 使用的可扩展的非阻塞式 web 服务器及其相关工具的开源版本.这个 Web 框架看起 ...
- 【BZOJ】1677: [Usaco2005 Jan]Sumsets 求和(dp/规律)
http://www.lydsy.com/JudgeOnline/problem.php?id=1677 完全背包很容易想到,将1,2,4...等作为物品容量即可. 然后这题还有一个递推式 f[i]= ...
- ejabberd
ejabberd是的Jabber / XMPP协议的即时通讯服务器,持牌GPLv2许可下(自由和开放源码) ,写的爱尔朗/检察官办公室.在其它特性中, ejabberd是跨平台,容错, cluster ...
- querySelectorAll 和getElementsByClassName的区别
querySelectorAll 返回的是映射 改变其值不会改变document 而getElementsByClassName 改变它就会改变document 摘自JavaScript权威指南(jQ ...
- 如何用ChemDraw选择结构
在使用ChemDraw软件过程中,我们往往会需要对结构进行翻滚.连结.旋转.分解.组合等操作.但是对于新手用户来说不是每种操作大家都会使用的. 针对这种情况我们会有一系列的教程来为大家讲解.下面我们就 ...
- VS2013和VS2010工具集和字符集
不兼容要改工具集 有时也要改字符集 位置:项目->项目属性->配置属性.常规 或者先选中项目,再同上. vs平台工具集 vs2010版本之后支持使用之前的版本编译,可以在 属性-> ...
