深度学习（四） softmax函数

softmax函数

softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类！

假设我们有一个数组，V，Vi表示V中的第i个元素，那么这个元素的softmax值就是

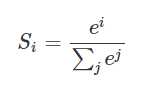
更形象的如下图表示：

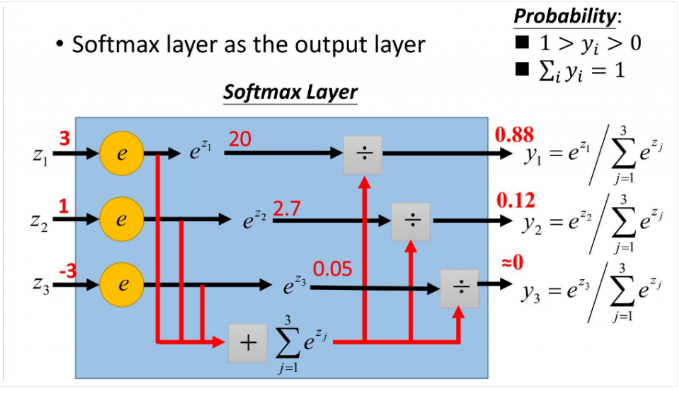
softmax直白来说就是将原来输出是3,1,-3通过softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标！

softmax相关求导

当我们对分类的Loss进行改进的时候，我们要通过梯度下降，每次优化一个step大小的梯度，这个时候我们就要求Loss对每个权重矩阵的偏导，然后应用链式法则。那么这个过程的第一步，就是对softmax求导传回去，不用着急，我后面会举例子非常详细的说明。在这个过程中，你会发现用了softmax函数之后，梯度求导过程非常非常方便！

下面我们举出一个简单例子，原理一样，目的是为了帮助大家容易理解！

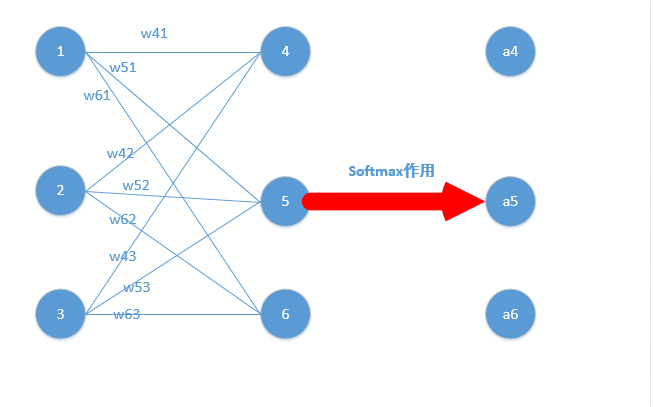
我们能得到下面公式：

z4 = w41*o1+w42*o2+w43*o3

z5 = w51*o1+w52*o2+w53*o3

z6 = w61*o1+w62*o2+w63*o3

z4,z5,z6分别代表结点4,5,6的输出，01,02,03代表是结点1,2,3往后传的输入.

那么我们可以经过softmax函数得到

$a_{4}= \frac{e^{z4} }{z^{z4}+z^{z5}+z^{z6}}$
$a_{5} =\frac{e^{z5} }{z^{z4}+z^{z5}+z^{z6}}$ $a_{6}= \frac{e^{z6} }{z^{z4}+z^{z5}+z^{z6}}$

好了，我们的重头戏来了，怎么根据求梯度，然后利用梯度下降方法更新梯度！

要使用梯度下降，肯定需要一个损失函数，这里我们使用交叉熵作为我们的损失函数，为什么使用交叉熵损失函数，不是这篇文章重点，后面有时间会单独写一下为什么要用到交叉熵函数（这里我们默认选取它作为损失函数）

交叉熵函数形式如下：

$Loss = -\sum_{i}^{}{y_{i}lna_{i} }$

其中y代表我们的真实值，a代表我们softmax求出的值。i代表的是输出结点的标号！在上面例子，i就可以取值为4,5,6三个结点（当然我这里只是为了简单，真实应用中可能有很多结点）

现在看起来是不是感觉复杂了，居然还有累和，然后还要求导，每一个a都是softmax之后的形式！

但是实际上不是这样的，我们往往在真实中，如果只预测一个结果，那么在目标中只有一个结点的值为1，比如我认为在该状态下，我想要输出的是第四个动作（第四个结点）,那么训练数据的输出就是a4 = 1,a5=0,a6=0，哎呀，这太好了，除了一个为1，其它都是0，那么所谓的求和符合，就是一个幌子，我可以去掉啦！

为了形式化说明，我这里认为训练数据的真实输出为第j个为1，其它均为0！

那么Loss就变成了 $Loss = -y_{j}lna_{j}$ ,累和已经去掉了，太好了。现在我们要开始求导数了！

我们在整理一下上面公式，为了更加明白的看出相关变量的关系：

其中 $y_{j} =1$ ,那么形式变为 $Loss = -lna_{j}$

那么形式越来越简单了，求导分析如下：

参数的形式在该例子中，总共分为w41,w42,w43,w51,w52,w53,w61,w62,w63.这些，那么比如我要求出w41,w42,w43的偏导，就需要将Loss函数求偏导传到结点4，然后再利用链式法则继续求导即可，举个例子此时求w41的偏导为:

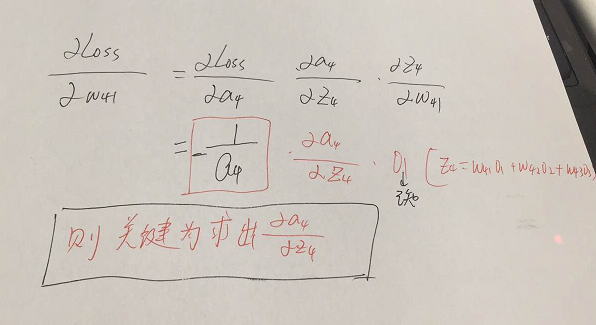
w51.....w63等参数的偏导同理可以求出，那么我们的关键就在于Loss函数对于结点4,5,6的偏导怎么求，如下：

这里分为俩种情况：

一：当选定的节点(我们要求误差项的节点)是我们期望的节点，则它的误差项为：

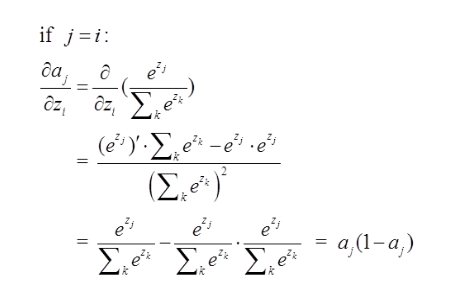
那么由上面求导结果再乘以交叉熵损失函数求导

$Loss = -lna_{j}$ ，它的导数为 $-\frac{1}{a_{j} }$ ,与上面 $a_{j}(1-a_{j} )$ 相乘为 $a_{j}-1$ （形式非常简单，这说明我只要正向求一次得出结果，然后反向传梯度的时候，只需要将它结果减1即可，后面还会举例子！）那么我们可以得到Loss对于4结点的偏导就求出了了（这里假定4是我们的预计输出）

二：当节点不上真正的期望节点，则它的误差项（梯度）求法如下：

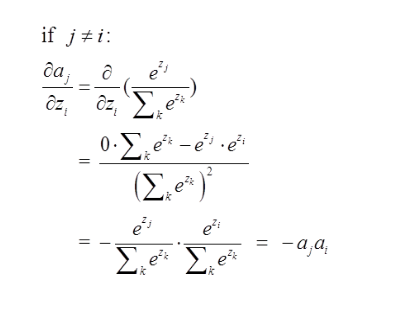
那么由上面求导结果再乘以交叉熵损失函数求导

$Loss = -lna_{j}$ ，它的导数为 $-\frac{1}{a_{j} }$ ,与上面 $-a_{j}a_{i}$ 相乘为 $a_{i}$ （形式非常简单，这说明我只要正向求一次得出结果，然后反向传梯度的时候，只需要将它结果保存即可，后续例子会讲到）这里就求出了除4之外的其它所有结点的偏导，然后利用链式法则继续传递过去即可！我们的问题也就解决了！

下面我举个例子来说明为什么计算会比较方便，给大家一个直观的理解

举个例子，通过若干层的计算，最后得到的某个训练样本的向量的分数是[ 2, 3, 4 ],
那么经过softmax函数作用后概率分别就是=[ $\frac{e^{2} }{e^{2}+e^{3}+e^{4}}$
, $\frac{e^{3} }{e^{2}+e^{3}+e^{4}}$ , $\frac{e^{4} }{e^{2}+e^{3}+e^{4}}$ ] = [0.0903,0.2447,0.665],如果这个样本正确的分类是第二个的话，那么计算出来的偏导就是[0.0903,0.2447-1,0.665]=[0.0903,-0.7553,0.665]，是不是非常简单！！然后再根据这个进行back propagation就可以了。