【bzoj4827】[Hnoi2017]礼物 FFT

题目描述

我的室友最近喜欢上了一个可爱的小女生。马上就要到她的生日了，他决定买一对情侣手 环，一个留给自己，一个送给她。每个手环上各有 n 个装饰物，并且每个装饰物都有一定的亮度。但是在她生日的前一天，我的室友突然发现他好像拿错了一个手环，而且已经没时间去更换它了！他只能使用一种特殊的方法，将其中一个手环中所有装饰物的亮度增加一个相同的自然数 c（即非负整数）。并且由于这个手环是一个圆，可以以任意的角度旋转它，但是由于上面 装饰物的方向是固定的，所以手环不能翻转。需要在经过亮度改造和旋转之后，使得两个手环的差异值最小。在将两个手环旋转且装饰物对齐了之后，从对齐的某个位置开始逆时针方向对装饰物编号 1,2,…,n，其中 n 为每个手环的装饰物个数，第 1 个手环的 i 号位置装饰物亮度为 xi，第 2 个手 环的 i 号位置装饰物亮度为 yi，两个手环之间的差异值为(参见输入输出样例和样例解释)： \sum_{i=1}^{n}(x_i-y_i)^2麻烦你帮他计算一下，进行调整（亮度改造和旋转），使得两个手环之间的差异值最小， 这个最小值是多少呢？

输入

输入数据的第一行有两个数n, m，代表每条手环的装饰物的数量为n，每个装饰物的初始 亮度小于等于m。

接下来两行，每行各有n个数，分别代表第一条手环和第二条手环上从某个位置开始逆时 针方向上各装饰物的亮度。

1≤n≤50000, 1≤m≤100, 1≤ai≤m

输出

输出一个数，表示两个手环能产生的最小差异值。

注意在将手环改造之后，装饰物的亮度 可以大于 m。

样例输入

5 6
1 2 3 4 5
6 3 3 4 5

样例输出

1

---

题解

FFT

首先，不用枚举c！

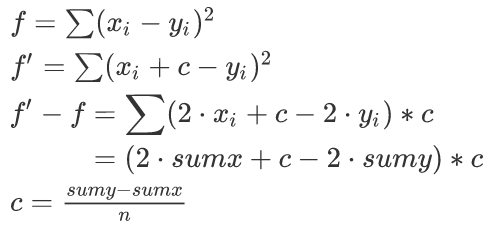
由于要求的是相对关系，所以给第二个手环+c就是给第一个手环-c。

设旋转后i位置分别为xi和yi，那么通过上面的式子可以得出c的最优取值与x和y的对应关系无关。

也就是说无论如何旋转，c的最优值总是固定的(sumy-sumx)/n（四舍五入到整数）

这样可以预处理出两个环的具体数值。

剩下的就交给FFT吧，将环倍增，所求即∑(x[i+k]-y[i])^2=∑x[i+k]^2 + ∑y[i]^2 - 2*x[i+k]*y[i]的最小值。

前两项可以预处理出来，最后一项同 bzoj2194 ，转化为卷积来求。

注意平方和不是和的平方。

#include <cstdio>
#include <cmath>
#include <algorithm>
#define N 1 << 20
#define pi acos(-1)
using namespace std;
struct data
{
	double x , y;
	data() {x = y = 0;}
	data(double x0 , double y0)  {x = x0 , y = y0;}
	data operator+(const data a)const {return data(x + a.x , y + a.y);}
	data operator-(const data a)const {return data(x - a.x , y - a.y);}
	data operator*(const data a)const {return data(x * a.x - y * a.y , x * a.y + y * a.x);}
}a[N] , b[N];
double sx[N] , sy[N];
void fft(data *a , int n , int flag)
{
	int i , j , k;
	for(i = k = 0 ; i < n ; i ++ )
	{
		if(i > k) swap(a[i] , a[k]);
		for(j = (n >> 1) ; (k ^= j) < j ; j >>= 1);
	}
	for(k = 2 ; k <= n ; k <<= 1)
	{
		data wn(cos(2 * pi * flag / k) , sin(2 * pi * flag / k));
		for(i = 0 ; i < n ; i += k)
		{
			data t , w(1 , 0);
			for(j = i ; j < i + (k >> 1) ; j ++ , w = w * wn)
				t = w * a[j + (k >> 1)] , a[j + (k >> 1)] = a[j] - t , a[j] = a[j] + t;
		}
	}
}
int main()
{
	int n , i , len;
	double c = 0 , ans = 10000000000 , sumx = 0 , sumy = 0;
	scanf("%d%*d" , &n);
	for(i = 0 ; i < n ; i ++ ) scanf("%lf" , &sx[i]) , c -= sx[i];
	for(i = 0 ; i < n ; i ++ ) scanf("%lf" , &sy[i]) , c += sy[i];
	c = round(c / n);
	for(i = 0 ; i < n ; i ++ ) sumx += (sx[i] + c) * (sx[i] + c) , sumy += sy[i] * sy[i];
	for(i = 0 ; i < 2 * n ; i ++ ) a[i].x = sx[i % n] + c;
	for(i = 0 ; i < n ; i ++ ) b[i].x = sy[n - i - 1];
	for(len = 1 ; len < 2 * n ; len <<= 1);
	fft(a , len , 1) , fft(b , len , 1);
	for(i = 0 ; i < len ; i ++ ) a[i] = a[i] * b[i];
	fft(a , len , -1);
	for(i = n - 1 ; i < 2 * n - 1 ; i ++ ) ans = min(ans , sumx + sumy - 2 * round(a[i].x / len));
	printf("%.0lf\n" , ans);
	return 0;
}