POJ2187 Beauty Contest（旋转卡壳）

嘟嘟嘟




旋转卡壳模板题。




首先求出凸包。

然后\(O(n ^ 2)\)的算法很好想，但那就不叫旋转卡壳了。

考虑优化：直观的想是在枚举点的时候，对于第二层循环用二分或者三分优化，但实际上两点距离是不满足单调性的，见下图：



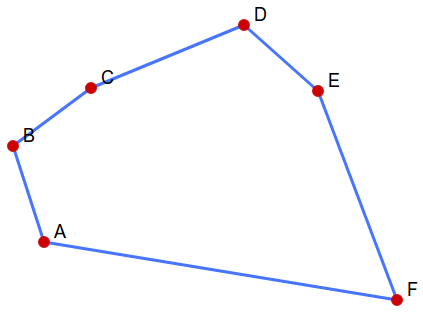
对于\(A\)点，\(AB < AC < AD > AE < AF\)。

那怎么办呢？

转换一下思路，如果枚举边，会发现每一个不在这条边上的顶点到边的距离是一个单峰函数！因此就能想到三分这个点，复杂度变成\(O(nlogn)\)。

不过实际上还可以优化，如果逆时针枚举的话，对于边\(e_i\)的下一条边\(e_{i + 1}\)，会发现到\(e_{i + 1}\)的最远点一定在\(e _ i\)的最远点的逆时针方向。换句话说，如果边是逆时针枚举的，那么最远点也是逆时针方向的。

因此维护两个指针，一个代表边，一个代表最远点。因为这两个指针最多转一圈，所以复杂度为\(O(n)\)。

一个优化就是判断距离的时候，因为底边是固定的，所以比较距离就是在比较三角形面积。（还能防止掉精度）

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<vector>
#include<stack>
#include<queue>
using namespace std;
#define enter puts("")
#define space putchar(' ')
#define Mem(a, x) memset(a, x, sizeof(a))
#define rg register
typedef long long ll;
typedef double db;
const int INF = 0x3f3f3f3f;
const db eps = 1e-8;
const int maxn = 5e4 + 5;
inline ll read()
{
  ll ans = 0;
  char ch = getchar(), last = ' ';
  while(!isdigit(ch)) last = ch, ch = getchar();
  while(isdigit(ch)) ans = (ans << 1) + (ans << 3) + ch - '0', ch = getchar();
  if(last == '-') ans = -ans;
  return ans;
}
inline void write(ll x)
{
  if(x < 0) x = -x, putchar('-');
  if(x >= 10) write(x / 10);
  putchar(x % 10 + '0');
}

int n;
struct Point
{
  int x, y;
  Point operator - (const Point& oth)const
  {
    return (Point){x - oth.x, y - oth.y};
  }
  int operator * (const Point& oth)const
  {
    return x * oth.y - oth.x * y;
  }
  friend inline int dis(const Point& A)
  {
    return A.x * A.x + A.y * A.y;
  }
  inline friend void swap(Point& A, Point& B)
  {
    swap(A.x, B.x); swap(A.y, B.y);
  }
}p[maxn], S;

bool cmp(Point A, Point B)
{
  int s = (A - S) * (B - S);
  if(s != 0) return s > 0;
  return dis(A - S) < dis(B - S);
}

int st[maxn], top = 0;
void Graham()
{
  int id = 1;
  for(int i = 2; i <= n; ++i)
    if(p[i].x < p[id].x || (p[i].x == p[id].x && p[i].y < p[id].y)) id = i;
  if(id != 1) swap(p[id], p[1]);
  S.x = p[1].x, S.y = p[1].y;
  sort(p + 2, p + n + 1, cmp);
  st[++top] = 1;
  for(int i = 2; i <= n; ++i)
    {
      while(top > 1 && (p[st[top]] - p[st[top - 1]]) * (p[i] - p[st[top - 1]]) < 0) top--;
      st[++top] = i;
    }
}

int area(Point A, Point B, Point C)
{
  return abs((A - B) * (A - C));
}
int nxt(int x)
{
  if(++x > top) x = 1;
  return x;
}
int rota()
{
  if(top == 2) return dis(p[st[1]] - p[st[2]]);
  int ret = 0;
  st[top + 1] = 1;
  for(int i = 1, j = 3; i <= top; ++i)
    {
      while(nxt(j) != i && area(p[st[i]], p[st[i + 1]], p[st[j]]) <= area(p[st[i]], p[st[i + 1]], p[st[j + 1]])) j = nxt(j);
      ret = max(ret, dis(p[st[i]] - p[st[j]]));
      ret = max(ret, dis(p[st[i + 1]] - p[st[j]]));
    }
  return ret;
}

int main()
{
  n = read();
  for(int i = 1; i <= n; ++i) p[i].x = read(), p[i].y = read();
  Graham();
  write(rota()), enter;
  return 0;
}