Fiber Network ZOJ 1967(Floyd+二进制状态压缩)

Description

Several startup companies have decided to build a better Internet, called the "FiberNet". They have already installed many nodes that act as routers all around the world. Unfortunately, they started to quarrel about the connecting lines, and ended up with every company laying its own set of cables between some of the nodes. 
Now, service providers, who want to send data from node A to node B are curious, which company is able to provide the necessary connections. Help the providers by answering their queries.

Input

The input contains several test cases. Each test case starts with the number of nodes of the network n. Input is terminated by n=0. Otherwise, 1<=n<=200. Nodes have the numbers 1, ..., n. Then follows a list of connections. Every connection starts with two numbers A, B. The list of connections is terminated by A=B=0. Otherwise, 1<=A,B<=n, and they denote the start and the endpoint of the unidirectional connection, respectively. For every connection, the two nodes are followed by the companies that have a connection from node A to node B. A company is identified by a lower-case letter. The set of companies having a connection is just a word composed of lower-case letters. 
After the list of connections, each test case is completed by a list of queries. Each query consists of two numbers A, B. The list (and with it the test case) is terminated by A=B=0. Otherwise, 1<=A,B<=n, and they denote the start and the endpoint of the query. You may assume that no connection and no query contains identical start and end nodes.

Output

For each query in every test case generate a line containing the identifiers of all the companies, that can route data packages on their own connections from the start node to the end node of the query. If there are no companies, output "-" instead. Output a blank line after each test case.

Sample Input

3
1 2 abc
2 3 ad
1 3 b
3 1 de
0 0
1 3
2 1
3 2
0 0
2
1 2 z
0 0
1 2
2 1
0 0
0

Sample Output

ab
d
-

z
-

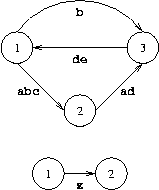
题目意思：n个路由器，编号1-n，26个公司，编号a-z，路由器之间有一些有向边，边权为一个字符串，字符串由小写字母组成，表示字符串对应的公司能使这条边连通。现在给若干个查询，查询能使任意2个路由器连通的公司。输出公司号，若不存在公司则输出‘-’。

解题思路：本题并不是求最短路，但是却要用到Floyd算法求解最短路的思想。题目就是要求能使任意2个路由器连通的公司的集合，所以可以使用Floyd传递闭包建立联系。另外，在本题中需要很巧妙地处理公司集合，公司是一个小写字母标识，最多只有26个公司，这样可以使用整数二进制位代表每个公司实现集合的状态压缩。

例如，站点1到站点2连接的公司有集合{ ‘a’ , 'b' ,  'c' }，可以用“00000000000000000000000111”表示，

站点2到站点3连接的公司有集合{ ‘a’ , 'd' } ，可以用“00000000000000000000001001”表示，

这两个整数进行二进制与运算后得到“00000000000000000000000001”表示通过中间站点2，站点1到站点3的连接的公司是集合{ ‘ a ’ }。

floyd的本质是枚举中间节点k，使节点i到j的距离最大或最小。针对本题，是要求一个集合，使从i到j连通的公司，那么枚举k的时候，就要求保证i->k和k->j同时连通的公司，状态压缩的话，直接将dis[i][k]和dis[k][j]相与便是结果，这个结果要加到dis[i][j]上去，所以再和dis[i][j]相或。所以总的方程就是：

dis[i][j] = dis[i][j] | (dis[i][k]&dis[k][j])。

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 int dis[][];
 int n,m;
 void Floyd()
 {
     int i,j,k;
     for(k=; k<=n; k++)
     {
         for(i=; i<=n; i++)
         {
             for(j=; j<=n; j++)
             {
                 dis[i][j]|=(dis[i][k]&dis[k][j]);
             }
         }
     }
 }
 int main()
 {
     int a,b,i;
     int len;
     char s[];
     while(scanf("%d",&n)!=EOF)
     {
         if(n==)
         {
             break;
         }
         memset(dis,,sizeof(dis));
         while(scanf("%d%d",&a,&b)!=EOF)
         {
             if(a==&&b==)
             {
                 break;
             }
             scanf("%s",s);
             len=strlen(s);
             for(i=; i<len; i++)
             {
                 dis[a][b]|=(<<(s[i]-'a'));///逻辑左移s[i]-'a'位
             }
         }
         Floyd();
         while(scanf("%d%d",&a,&b)!=EOF)
         {
             if(a==&&b==)
             {
                 break;
             }
             if(dis[a][b])
             {
                 for(i=; i<; i++)
                 {
                     if(dis[a][b]&(<<i))///如果dis[a][b]&(1<<i)！=0，说明dis[a][b]所代表的集合中包含公司'a'+i
                     {
                         putchar('a'+i);
                     }
                 }
             }
             else
             {
                 putchar('-');
             }
             putchar('\n');
         }
         putchar('\n');
     }
     return ;
 }