buaacoding_2018算法期末上机G题.地铁建设题解

// 标注：本文旨在为博主确立一种题解的基本范式，以避免博主的题解流于AC代码的粘贴。此基本范式为：完整而简洁明了的思路及其推导说明，力图触及问题的本质并衍生对同类问题的思路分析，使得题解具有泛用性，同时可以写出对代码的优化过程。

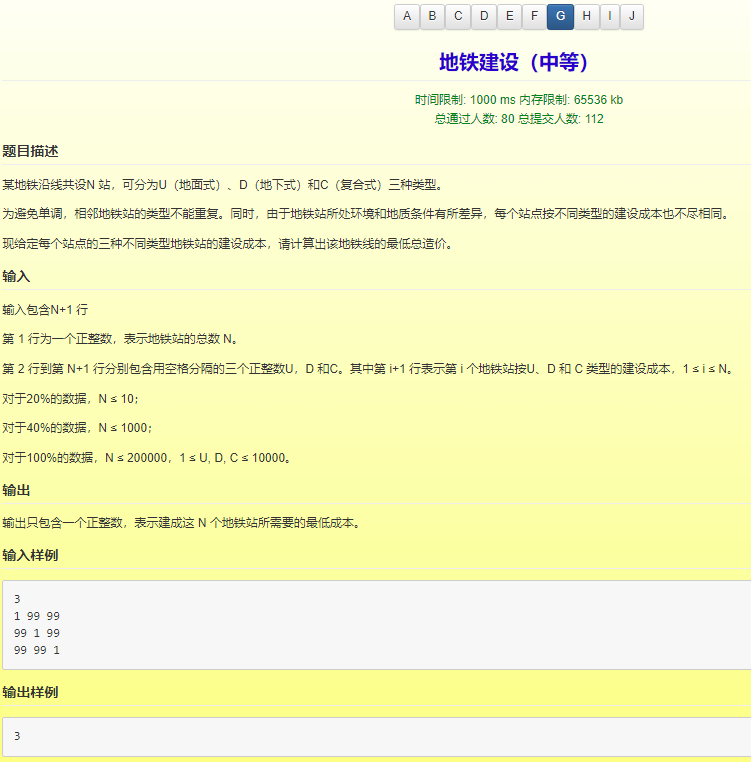
简单题，流水线问题的变形： \(U、D、C\)是三条流水线，每次步进都要转换到别的流水线上，其中 \(U[i]、D[i]、C[i]\) 就是转换到对应类型的流水线的第 \(i\) 个元素的成本，求最小总成本 \(^{①}\)

假设 \(f(i)\) 为对前 \(i\) 个元素构成的子问题的最优解集， \(f(i;U)\) 为以 \(U\) 类型为终点的前 \(i\) 个元素构成的子问题的最优解，\(f(i;D)\)、\(f(i; C)\) 同理。 \(^{②}\)

以 \(U[i], D[i], C[i]\) 表示第 \(i\) 个地铁站对应类型的建设成本

不妨设\(f(0;U) = f(0;D) = f(0;C) = 0\)

而且初始值 \(f(1;U) = U[1]\) 、 \(f(1;D) = D[1]\) 、 \(f(1;C) = C[1]\)

定义好状态转移方程的属性之后，结合题意(①)以及 \(f(i)\) 的意义(②)，可得状态转移方程：

\[\begin{equation}
f(i) =
\left\{
\begin{array}{**lr**}
f(i;U) &=& min\{f(i-1;D), f(i-1; C)\} + U[i] \\
f(i;D) &=& min\{f(i-1;U), f(i-1; C)\} + D[i] \\
f(i;C) &=& min\{f(i-1;U), f(i-1; D)\} + C[i]
\end{array}
\right.
\ \ \ \ \ ,\ i = 1,2,3, \dots, n
\end{equation}
\]

简化就是： \(dp[i][type] = min\{dp[i-1][t] \text{ | t} \in (S-\{type\})\}+cost[i][type] \text{ , 其中 }type\in S = \{U,D,C\}\)

构造出状态转移方程，就可以写代码了。

代码流程：

• 用Subway结构体存储每个地铁站的不同类型的建设成本，然后用一个subway数组存储所有地铁站的不同类型的建设成本
• 然后遍历subway数组并用状态转移方程进行状态转移（记得将dp数组初始化为0，以避免上组数据的影响）
• 最后dp[n][u], dp[n][d], dp[n][c]中最小值即为结果。

时间复杂度为 \(O(n)\)

空间复杂度为 \(O(n)\) , 具体大约是 \(7n\) ，开了两个大数组，7 * MAXN * sizeof(long long) 容易MLE（特别是对于long long 癌）

#include <cstdio>
#include <cstring>
#include <algorithm>
#define LL long long
using namespace std;

const int MAXN = 200005;
struct Subway{
    LL U;
    LL D;
    LL C;
}subway[MAXN];

LL dp[MAXN][4];
const int u = 1, d = 2, c = 3;

int main(){
    LL n;
    while(~scanf("%lld", &n)){
        memset(dp,0,sizeof(dp));
        for(int i = 1; i <= n; i++) {
            scanf("%lld%lld%lld", &subway[i].U, &subway[i].D, &subway[i].C);
        }

        for(int i=1;i<=n;i++){
            dp[i][u] = min(dp[i-1][d],dp[i-1][c])+subway[i].U;
            dp[i][d] = min(dp[i-1][u],dp[i-1][c])+subway[i].D;
            dp[i][c] = min(dp[i-1][u],dp[i-1][d])+subway[i].C;
        }

        LL ans = min(dp[n][u],dp[n][d]);
        ans = min(ans, dp[n][c]);
        printf("%lld\n", ans);
    }
    return 0;
}

对比两个for循环，我们发现其实两个for循环的每一步其实是对应的，也就是说，每个subway[i]只在第i次循环中被调用，所以我们可以考虑将两个循环合并成一个。

for(int i = 1; i <= n; i++) {
    scanf("%lld%lld%lld", &subway[i].U, &subway[i].D, &subway[i].C);

    dp[i][u] = min(dp[i-1][d],dp[i-1][c])+subway[i].U;
    dp[i][d] = min(dp[i-1][u],dp[i-1][c])+subway[i].D;
    dp[i][c] = min(dp[i-1][u],dp[i-1][d])+subway[i].C;
}

合并循环之后发现，每组subway[i].U，subway[i].D, subway[i].C都是只在该次循环用到，以后不会再用了；而且由于是合在一个循环里，我们没有必要把它存起来以在第二个循环重新调用。也就是说，在这种情况下subway这个数组和Subway结构体的定义完全是多余的，我们完全可以直接删掉，改成用U、D、C三个变量当缓存就行了。

合循环、去数组，这样子我们就将时间复杂度和空间复杂度都降低了一半左右。

时间复杂度为 \(O(n)\)

空间复杂度为 \(O(n)\) , 具体大约是 \(4n\)

#include <cstdio>
#include <cstring>
#include <algorithm>
#define LL long long
using namespace std;

const int MAXN = 200005;
LL dp[MAXN][4];
const int u = 1, d = 2, c = 3;

int main(){
    LL n;
    while(~scanf("%lld", &n)){
        LL U,D,C;
        memset(dp,0,sizeof(dp));
        for(int i = 1; i <= n; i++) {
            scanf("%lld%lld%lld", &U, &D, &C);

            dp[i][u] = min(dp[i-1][d] , dp[i-1][c]) + U;
            dp[i][d] = min(dp[i-1][u] , dp[i-1][c]) + D;
            dp[i][c] = min(dp[i-1][u] , dp[i-1][d]) + C;
        }
        LL ans = min(dp[n][u],dp[n][d]);
        ans = min(ans, dp[n][c]);
        printf("%lld\n", ans);
    }
    return 0;
}

那么，还能不能再优化呢？当然可以！

看上面的代码，会发现dp[i]只与dp[i-1]有关，是Markov链，无后效性，dp[i-2]及以前的都无用了，那么我们可以考虑用滚动数组来改进程序。

简单来说，滚动数组就是让数组滚动起来，每次都使用固定的几个存储空间，来达到压缩，节省存储空间的作用。

可以看到，用滚动数组改进之后的程序在空间上不再受n的限制，无论n多大都能处理，有效防止MLE。

时间复杂度为 \(O(n)\) （时间复杂度是改不动的，虽然可以用计组的知识继续优化，但是没多大效果）

空间复杂度为 \(O(1)\)

（另外const int u = 1, d = 2, c = 3;能帮助你在编写程序的过程中更容易地理清思路）

#include <cstdio>
#include <cstring>
#include <algorithm>
#define LL long long
using namespace std;

LL dp[2][3];
const int u = 0, d = 1, c = 2;

int main(){
    int n;
    while(~scanf("%d", &n)){
        dp[0][u] = dp[0][d] = dp[0][c] = 0;
        LL U,D,C;
        for(int i = 1; i <= n; i++){
            scanf("%lld%lld%lld", &U, &D, &C);

            dp[1][u] = min(dp[0][d], dp[0][c]) + U;
            dp[1][d] = min(dp[0][u], dp[0][c]) + D;
            dp[1][c] = min(dp[0][u], dp[0][d]) + C;

            dp[0][u] = dp[1][u];
            dp[0][d] = dp[1][d];
            dp[0][c] = dp[1][c];
        }
        LL ans = min(dp[0][u], dp[0][d]);
        ans = min(ans, dp[0][c]);
        printf("%lld\n", ans);
    }
    return 0;
}

至此，主要的优化工作就结束了。

最后，如果不是老手的话直接想到最后一个版本还是有些难度的，所以一开始不妨先想个naïve(暴力)点的版本再逐模块地优化。